前言
第一单元的作业是对多项式进行求导,有三次作业,每一次作业的难度逐步递增。性能分均由输出表达式的长度决定。
第一次作业——简单多项式求导
一、需求分析与设计思路简述
-
输入:仅含有幂函数的,格式合法的多项式字符串
-
输出:格式合法的多项式字符串
第一次作业是要对仅含有幂函数的多项式进行求导。由于仅有一种基本函数,所以程序结构也比较简单。
多项式是由项构成,每一项又只有一个带系数的幂函数,所以多项式可以用HashMap来进行维护。这样合并同类项和求导都比较方便。
对输入的处理也可以进行分层处理。先将空白字符删去,然后将多项式切割成一个个项,分别对项进行正则匹配读取。然后将解析之后的项加到多项式里面。
输出的格式化可以在toString
二、代码质量分析
-
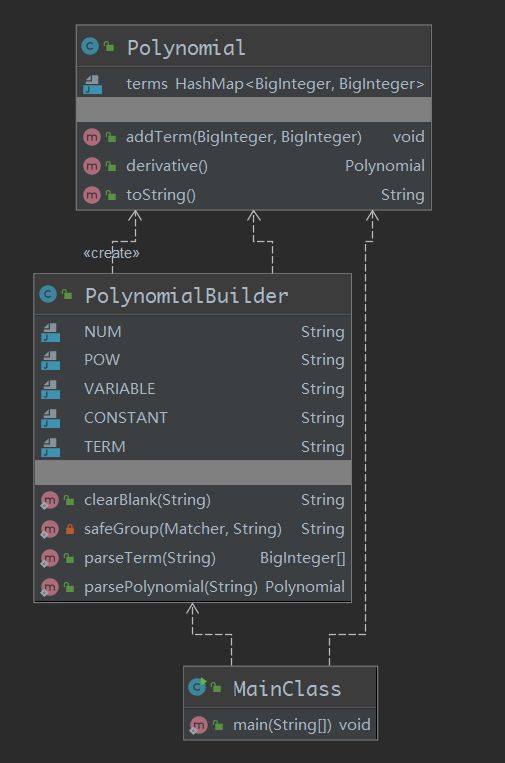
类图
从类图可以看出,类的依赖关系比较简单。这里就不多bb了。
-
方法复杂度
Method ev(G) iv(G) v(G) LOC elements.Polynomial.toString() 4 13 14 50 elements.PolynomialBuilder.parseTerm(String) 1 6 8 36 elements.PolynomialBuilder.parsePolynomial(String) 1 3 3 15 elements.PolynomialBuilder.safeGroup(Matcher,String) 2 2 4 15 elements.Polynomial.addTerm(BigInteger,BigInteger) 1 4 4 14 elements.PolynomialBuilder.clearBlank(String) 1 2 2 9 elements.Polynomial.derivative() 1 2 2 7 main.MainClass.main(String[]) 1 1 1 6 elements.Polynomial.Polynomial() 1 1 1 3 参数解释:
v(G): 计算每种非抽象方法的圈复杂度。 循环复杂度是对每种方法中不同执行路径数量的度量。 这也可以被视为完全执行方法的控制流程所需的最少测试次数。 实际上,它的值是 if数,while数,for数,do数,方法中的case转换,catch,条件表达式,&&的和||的数量之和+1。
iv(G): 计算方法的设计复杂度。 设计复杂性与方法控制流与对其他方法的调用之间如何关联有关。 设计的复杂性的范围从1到v(G)。 设计复杂度还代表了将方法与调用的方法进行集成所需的最少测试次数。
ev(G): 计算每种非抽象方法的基本复杂度。 基本复杂度是一种图形理论上的度量,用于衡量方法的控制流结构的不良程度。 基本复杂度范围从1到v(G)。
LOC: 计算方法代码行数。
从表格上看,由于输出处理全部都在
toString这个方法,而且输出有一些细节的优化,导致toString方法分支过多,过于臃肿,各项指标均超标。现在回来看这个方法,其实有很多的问题,均可以通过重构解决。另外
parseTerm这个处理项字符串的方法,也存在分支过多的问题,需要进一步分解。 -
类复杂度
Class CSA CSO LOC OCavg OSavg WMC elements.PolynomialBuilder 5 16 82 3.75 11.5 15 elements.Polynomial 1 16 77 5.25 11.25 21 main.MainClass 0 13 8 1 4 1 参数解释:
CSA: 计算每个类的属性(或字段)总数。
CSO: 计算每个类的操作(或方法)总数。
LOC: 计算类代码行数。
OCavg: 计算每个类中非抽象方法的平均圈复杂度。
OSavg: 计算每个类中非抽象方法的平均大小。 方法的大小以其包含的语句数计算。
WMC: 计算每个类中方法的总循环复杂度。
从表格来看,
PolynomialBuilder和Polynomial的平均圈复杂度都稍有偏高,主要原因是两个类当中都有一个臃肿的方法。所以问题还是归结到重构那两个方法。 -
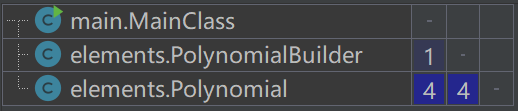
类依赖矩阵
从依赖矩阵来看,类之间的依赖还不算太深。Polynomial作为主要功能类,必然是被依赖最多的类。
三、Bug分析
第一次作业的bug是无法正确识别--x这样的表达式。原因是识别时的所用的正则表达式是完全对照着指导书的,没有及时照着讨论区所说的更正。
四、测试策略
第一次作业的测试策略是依靠评测机和静态代码测试的策略。
评测机是用python+命令行搭建的。python主要用于搭建数据生成器和正确性测试。命令行负责统筹一切以及完成从输入获得待测试输出的过程。但是,由于数据生成器中的正则表达式也是对照指导书生成的,所以测不出我原来代码的bug。
评测机采用的策略是随机数据+固定数据混合测试的策略。
静态代码测试就是通过读别人的代码来发现别人的bug,我确实通过阅读别人代码,发现了评测机不容易测出来的bug。而且可以通过这种方法进行构造数据。
五、对象创建模式的应用
FactoryBuilder这个类就有点使用工厂模式的意思了,不过还是有步骤不够明确,方法不够简练的问题。
第二次作业——支持包括简单三角函数幂次和乘积项的多项式求导
一、需求分析与设计思路简述
-
输入:包括幂函数和三角函数幂次的,格式合法的多项式字符串
-
输出:格式合法的多项式字符串
这次的作业相对于上一次多了三角函数和乘积项求导。由于在很多方面都需要做改变,所以我干脆放弃了重构,直接从头开始。
对象的构造方式发生了变化,变成了表达式项因子的三层结构。项内仍然使用HashMap进行维护,为了方便化简,表达式也利用HashMap进行维护。
输入的处理思路与上一次作业大体相同,只不过多了一层处理罢了。
输出的思路有些改变,这一次因为结构上出现了分层,所以输出也采用了分层处理的方式,每一层都有自己的输出处理。
二、代码质量分析
-
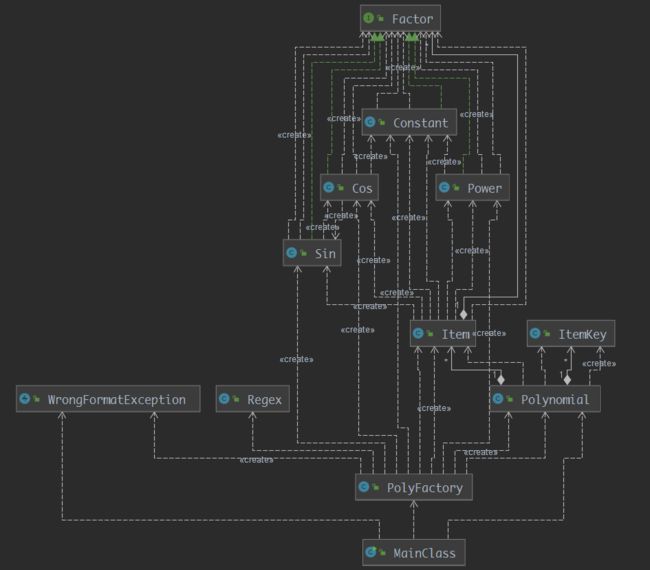
类图
从图来看,层次关系还是有一点的,但是不同因子之间还是存在依赖关系,比如
Constant被Cos和Power依赖。这些都是因为求导过程中会出现其他类型的因子。但是
Item对各种因子都出现了依赖,这并不是一个好现象。检查代码发现主要的依赖均出现在优化模块。真是为了优化放弃架构了如果要重构的话可以注重在这个模块。 -
方法复杂度
由于方法过多,这里只展示一部分。
Method ev(G) iv(G) v(G) LOC poly.Item.merge(Item) 13 18 25 51 factory.PolyFactory.parseFactor(String) 8 3 9 32 poly.Item.toString() 4 5 7 25 poly.Polynomial.simplify() 7 7 8 25 poly.Item.multiplyFactor(Factor,BigInteger) 4 5 6 21 poly.ItemKey.equals(Object) 6 2 6 21 factory.PolyFactory.parseItem(String) 2 5 6 18 main.MainClass.main(String[]) 2 3 3 18 poly.Item.derivative() 1 5 5 18 factory.PolyFactory.parsePoly(String) 3 2 4 17 poly.Polynomial.toString() 3 3 4 17 相比上一次作业,这一次作业的输入方法处理多了一层,单个方法的臃肿程度也稍有缓解,但是还是存在分支较多的问题。输出的问题也由于分解到各层而分散了。
但是这次作业出现了一个比较严重的问题,就是优化模块
merge方法过于粗暴,导致各项指标严重超标。simplify也有分支过多的问题,重构的时候可以从这两个方面入手。
-
类复杂度
Class CSA CSO LOC OCavg OSavg WMC poly.Item 3 23 172 4.82 9.82 53 factory.PolyFactory 0 16 80 4.75 12 19 poly.Polynomial 1 17 69 3.8 8 19 poly.ItemKey 1 15 38 3.33 7.33 10 factor.Cos 0 20 28 1.4 1.8 7 factor.Power 0 20 28 1.4 1.8 7 factor.Sin 0 20 28 1.4 1.8 7 factor.Constant 1 21 25 1 1 6 main.MainClass 0 13 20 2 12 2 constant.Regex 11 12 15 n/a n/a 0 factory.PolyFactory.FactorStruct 2 13 8 1 2 1 factory.WrongFormatException 6 42 2 n/a n/a 0 从表格来看,
Item类是个“大块头”,主要是因为里面有一些“大块头”方法。优化使人头大其次就是输入处理,可以看情况再进行一次分解。
-
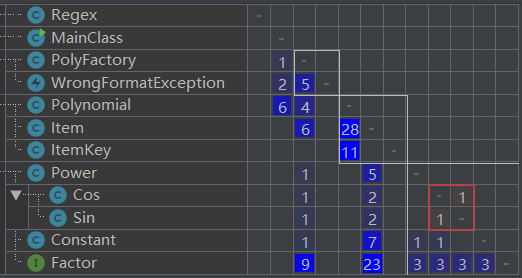
依赖矩阵
从图中可以看出,
Polynomial对Item和ItemKey,Item对Factor都有很深的依赖,明显反映了层次关系。但是Item对各种Factor都有或浅或深的依赖,这说明了类与类之间还需要进一步脱耦。这里还有一个循环依赖:
Cos和Sin。我在设计的时候就考虑过要不要将它们合在一起,不过后来还是决定分开了。这里的循环依赖是因为求导的问题。除了上述循环依赖,矩阵的右上部分没有出现依赖情况,说明代码没有严重的循环依赖问题。
三、Bug分析
第二次作业的bug有两个。
第一个是优化模块计算错误导致的bug,测试匆忙,没有覆盖全面。
第二个是没有将除 ‘ ’ 和 ‘\t’ 之外的其他空白字符认定为非法字符。小学老师没教过你认真读题吗?
四、测试策略
这次由于做得匆忙,测试策略基本沿袭上一次作业的策略。不过静态代码测试减少了(太摸了)。评测机只换了正则表达式,所以测试做得不是很到位。
不过由于强测分低,匹配到的同学几乎都有bug,所以这样的测试也测到了不少的bug
五、对象创建模式的应用
跟上一次作业差不多,PolyFactory担任了工厂的角色,不过有些臃肿。
第三次作业——支持包括简单三角函数幂次、乘积项、嵌套的多项式求导
一、需求分析与设计思路简述
-
输入:格式合法的多项式字符串
-
输出:格式合法的多项式字符串
这次作业仅比上一次多了一个表达式因子和三角函数的嵌套规则,但是难度有了显著的提升。在一片改用表达式树架构的喧哗声中,我决定坚持上一次作业的架构,通过重构来完成这一次作业。
为了支持表达式因子,我让Polynomial也继承Factor接口。
为了支持嵌套,我在三角函数类中增加一个content属性。
这样的话外层的HashMap可能就需要改动了。由于规模的减小和种类的增多,用List的开销在可接受范围之内,而实现起来也比Map方便,所以我改用List来维护一个表达式了。
对输入的处理策略需要变化。因为嵌套规则,不能用正则表达式一下子匹配整个输入了。但是我可以从最简单的不包含嵌套的表达式开始匹配,由里向外逐步处理一个复杂的表达式。至于简单表达式的匹配,那就几乎与上一次作业相同了。
对输出的处理没有太大的变化,依旧是各层做好自己的toString即可。
至于优化,我这次作业采取了更加谨慎的策略,放弃了作业二“大块头”优化,只是做了简单的合并同类项和去括号处理,不过从结果来看,这样已经足够了。
二、代码质量分析
-
类图
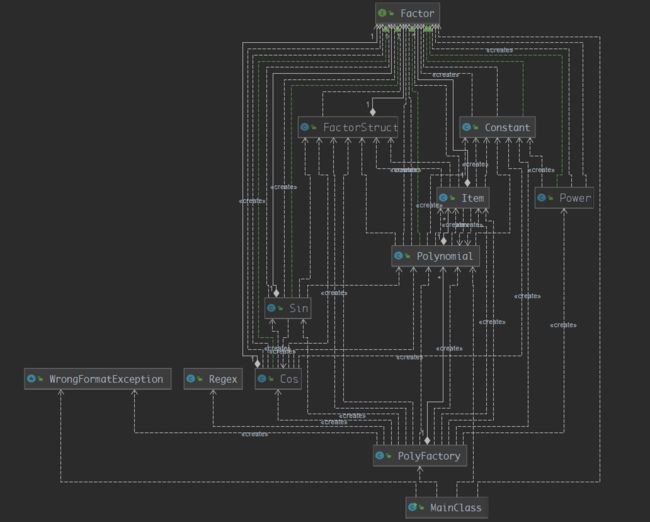
从类图上看,
(你看,你还看,再看你就瞎了)各类因子之间的耦合变得十分严重。Polynomial与Item纠缠不清,你中有我,我中有你。三角函数跟Polynomial也有了纠葛。这些纠纷,大部分都是优化的锅。不过对于优化带来的严重耦合,我也没有比较好的方法。 -
方法复杂度
由于方法过多,以下仅展示行数超过15的方法。
Method ev(G) iv(G) v(G) LOC factory.PolyFactory.parseFactor(String) 11 7 12 43 poly.Item.multiplyFactor(Factor,BigInteger) 7 10 11 34 poly.Item.toString() 4 5 7 32 poly.Polynomial.addItem(Item) 6 9 10 31 poly.Item.merge(Item) 1 6 6 29 factory.PolyFactory.parsePoly(String) 3 2 4 27 poly.Polynomial.toString() 5 6 7 25 factory.PolyFactory.parseItem(String) 2 5 6 18 main.MainClass.main(String[]) 2 3 3 18 poly.Item.derivative() 1 5 5 18 poly.Polynomial.toSimpleFactor() 2 5 6 18 factor.Cos.toString() 4 4 4 17 factor.Sin.toString() 4 4 4 17 poly.Item.equals(Object) 5 3 7 17 由表格可以看出,这一次作业优化导致的分支多的弊病还是十分突出。感觉优化处理应该要做得更加好才行。
-
类复杂度
Class CSA CSO OCavg OSavg WMC LOC poly.Item 3 27 3.33 7.53 50 262 poly.Polynomial 1 28 3.18 6.73 35 156 factory.PolyFactory 1 18 4.33 12 26 118 factor.Cos 1 25 1.75 3.38 14 60 factor.Sin 1 25 1.75 3.25 14 59 factor.Constant 1 26 1.33 1.67 12 46 factor.Power 0 24 1.29 1.57 9 36 main.MainClass 0 13 2 10 2 20 constant.Regex 13 12 n/a n/a 0 18 factor.FactorStruct 2 15 1 1.33 3 14 factory.WrongFormatException 6 42 n/a n/a 0 2 Item这个类有些臃肿了,超过了200行,有10+个方法,需要进一步的分解。其次是Polynomial和PolyFactory这两个类,也都超过了100行,Polynomial的方法数比Item还要多,也是应该把一些功能分派出去了。另外,这三个类的平均圈复杂度也比较高。说明需要对这三个类的方法进行一些重构了。
-
依赖矩阵
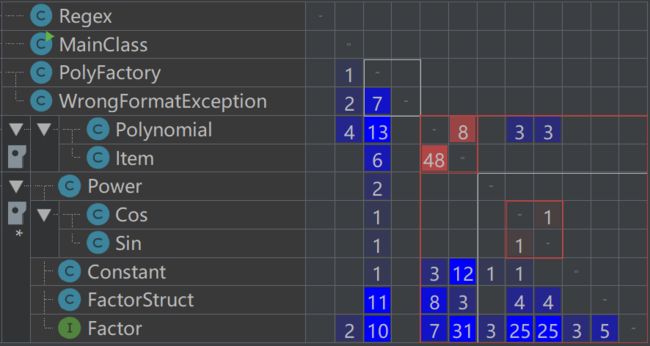
从依赖矩阵中,可以看到因子之间严重的依赖,和
Polynomial与Item之间的循环依赖。我在做这个项目的时候,也一直不知道该如何处理好这两个类之间的关系:Polynomial作为一个因子时,是Item的一部分,而Item又是Polynomial的一部分。可能是这个架构本身的问题吧,希望如果有dalao看到能够不吝赐教。
三、Bug分析
这次的Bug还是出现在优化上面,一个是没有注意到对象的可变性的问题,在对可变对象的遍历的时候不经意改变了对象的属性,造成错误。而且这个错误还是后来砸了6w数据才测出来的(可能我的评测机比较菜吧),在一般情况下不会出现,只有在极少数情况才会出现。
另一个是在表达式去括号的时候没有正确处理 (x+1)*(x+1) 这样的情况。因为我是用HashMap维护的项,两个相同的因子相乘时会合并,但是去括号的时候漏了考虑指数,直接就把表达式因子取出来了,结果出现问题。
四、测试策略
这次的测试我完全使用评测机进行测试,对异常数据进行人工检验。这一次我对评测机进行了改进,抛弃了不熟悉的命令行,完全使用python完成对评测机的搭建,并且评测机可以同时对多个项目进行评测,提高了评测效率。
另外,我通过分析评测机,发现评测时间大部分都花在了启动待评测的JAVA项目上。于是我就对每个项目做了一些改造,使得它们都支持多行输入,并且对每行输入都产生相应的输出,这样的话,就可以减少启动的次数。果然,做了改进之后,评测效率提高了10倍以上。
但是,我在互测时依然被hack出来,说明我的评测机还有要改进的地方。同时,由于我的评测机没有检测输出的合法性,导致我在互测当中错过发现别人bug的机会。我要从这个单元的学习中汲取经验,争取在下个单元做出更好的测试。
五、对象创建模式的应用
与上一次作业差不多,不过内部实现的方法有所不同。如果要重构的话,可以考虑分层实现工厂,使用抽象工厂进行脱耦。
总结与反思