思路
要素察觉:必须要是一个公差为 \(d\) 的等差数列。
特判
首先要特判掉 \(d=0\) 的情况,这样的情况下就是要寻找最长的一段数字相同的区间,找到之后输出左右端点即可(可以 \(O(n)\) 扫一遍)。
其他情况
再来看别的情况,对于一个区间 \([l,r]\),如果要满足是一个公差为 \(d\) 的等差序列,那么:
- 这个等差数列里的所有数 \(\bmod d\) 的结果应该一样.
- 区间内没有重复的数.
现在考虑如何实现上述条件:
-
首先将序列分成若干个 \(x \bmod d\) 都一样的子区间。
在从左往右扫的过程中,如果遇到了与前面 \(x\bmod d\) 的值不同的数,就将左边 \(x\bmod d\) 值相同的数作为一个独立的区间来处理,这样就可以把序列分成若干个 \(x \bmod d\) 都一样的区间。
-
对于一个满足 \(x\bmod d=c\) 的数列,把所有的 \(x\) 变成 \(\dfrac{x-c}{d}\) (因为整形的性质,可以直接除)。
这一步称之为归一化,实现了将一个区间的的公差化为 \(1\),
问题就转化成了加入 \(k\) 个数,使区间排序后公差为 \(1\)。
-
对于一个区间 \([L,R]\),算出最少加几个数。
需要满足的条件显然就是不能有重复,那么最少加的数的个数就是 \(\max(L,R)-\min(L,R)+1-(R-L+1)\)。
-
从小到大枚举 \(R\)。
那么问题就相当于求最小的 \(L\),使得
-
\([L,R]\) 无重复。
从小到大枚举 \(R\),对于新的 \(a[R]\) 很容易知道它前面一个和他相等的数 \(a[T]\) (可以用\(map\)实现),那么 \(L\) 至少要大于 \(T\)。
-
加的数不能多于 \(k\) 个。
也就是 \(\max(L,R)-\min(L,R)+1-(R-L+1)\le k\),转化一下即 \(\max(L,R)-\min(L,R)+L\le k + R\),
用线段树维护 \(w[L]=\max(L,R)-\min(L,R)+L\),
假如 \(L\) 的下界是 \(T\),那么我们要在 \([T+1,R]\) 中找最左的位置使得 \(w\le k + R\)。
如果能完成上述过程,这道题就做完了,那么现在的问题是,如何维护 \(w\)。
维护 \(w\)的方法
用单调栈。维护一个单调递减的栈和一个单调递增的栈,两个栈的维护方法是同理的,此处以单调递减的栈为例进行讲解。
因为单调栈递减的性质,所以当一个大于栈顶的元素加入时,会不断地弹出栈顶,直到栈顶元素大于此元素为止,再将此元素入栈,由此,单调栈可以将 \(\max(L,R)\) 分成递减的若干段,考虑是如何实现的:
-
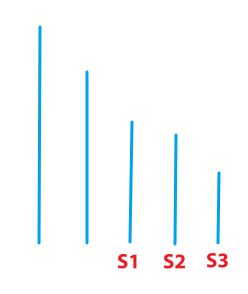
如图所示,假设有一个单调递减的单调栈,其中 \(S1> S2> S3\),\(S3\) 为栈顶元素。
-
由于单调栈的性质,\(S1\) 和栈中上一个元素之间可能是有别的元素的,所以 \(S1,S2,S3\) 其实代表了三个区间的最大值。
-
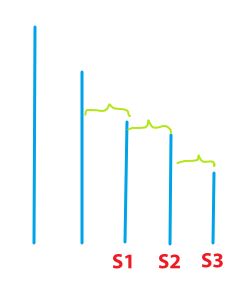
此时,单调栈中来了一个新的元素 \(a\),显然 \(a>S1>S2>S3\),为了维护单调栈的性质,所以我们要将 \(S1,S2,S3\) 弹栈。

-
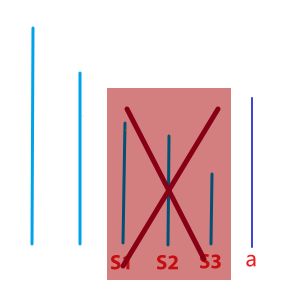
在弹栈时,因为此时这三个元素的值不能代表上述三个段的最大值了,所以我们需要将三个段的贡献从线段树中减去。
-
同时,新的元素 \(a\) 就加进来了,这个时候就可以发现原来三个段的代表元素被弹出之后,其实就被新元素所接管了,整个区间的最大值变成 \(a\) 元素的值,所以再对一整个区间进行区间加操作。

这样单调栈就实现了将 \(\max(L,R)\) 分成了递减的若干段,由此就可以不断进行段树的区间加、区间减。
\(\min\) 的维护与 \(\max\) 同理。
总时间复杂度 \(O(n\log n)\)。
代码
/*
Author:loceaner
线段树,单调栈
*/
#include




