程序结构分析
第一次作业
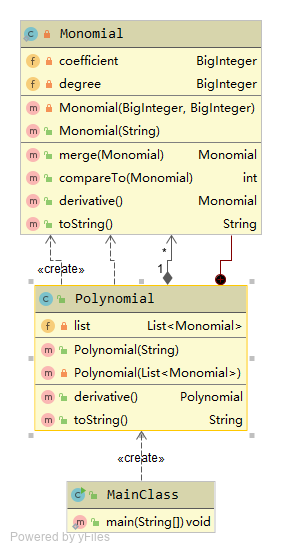
第一次作业较为简单,根据多项式由多个项构成的描述,可以抽象出两个类——多项式、项。多项式的求导结果便是其各个项的求导结果之和。
项类持有两个 BigInteger 对象(项的系数和指数)。项类实现 Comparable 接口,从而可以根据两个项的比较结果判定两个项是否为同类项(可合并)。项类配备求导方法,返回一个新的项。
多项式类持有一个 List 对象,存储其各个项。多项式类配备求导方法,返回一个新的多项式。
第一次作业读入处理:使用正则表达式直接提取各个项。
类图:
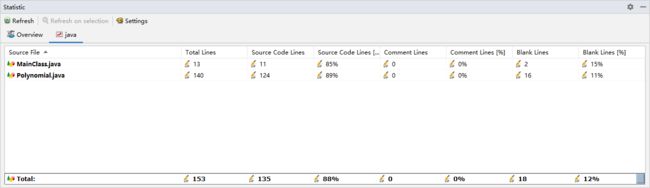
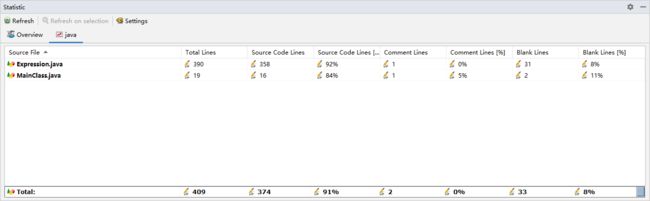
代码行数:
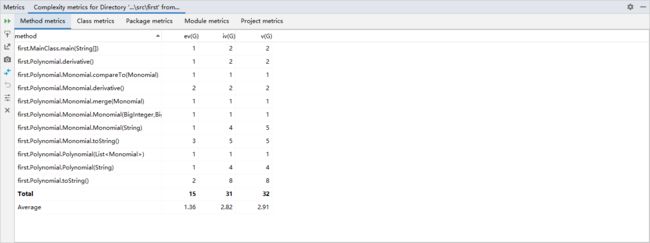
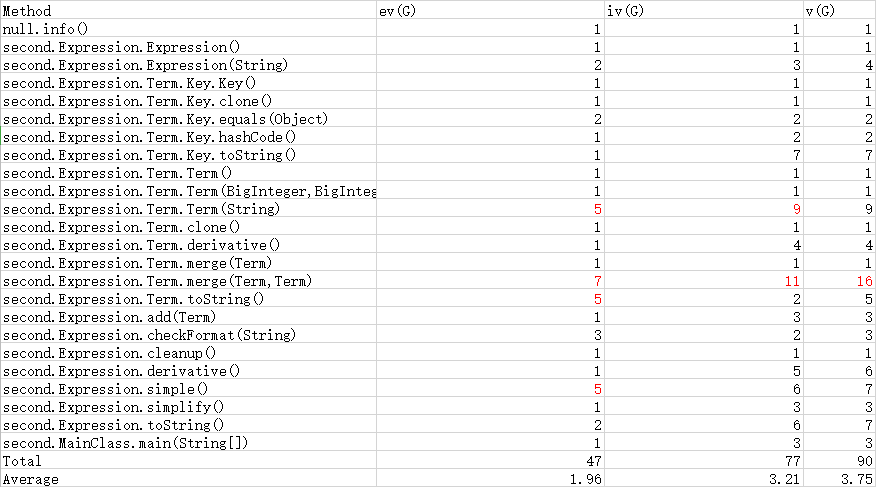
方法复杂度:
第二次作业
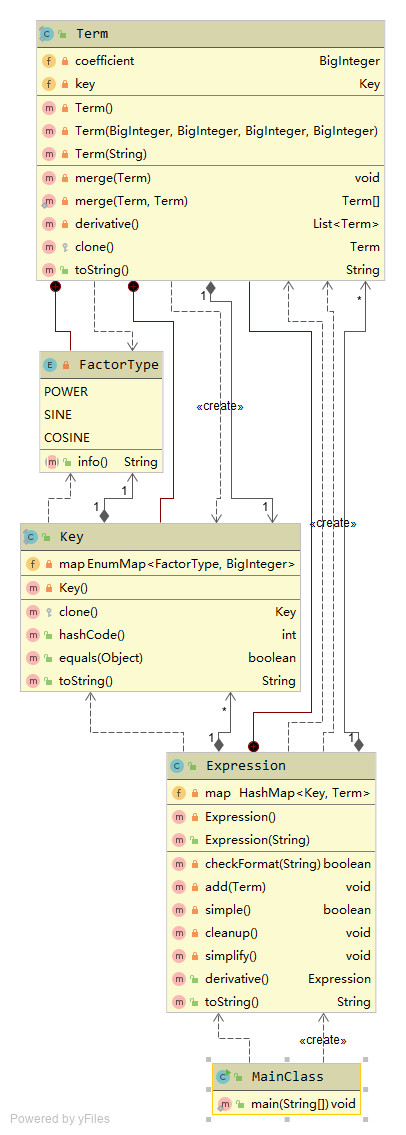
第二次作业出现了三角函数因子,理论上可以抽象出因子类的概念,但考虑到第二次作业存在优化问题,以及一个项的一般形式可以表示为 a*x**b*sin(x)**c*cos(x)**d ,故使用一个四元组来构成一个项。考虑到两个项是否可合并取决于两个项的指数部分是否对应相等,故将指数部分封装成类,覆写其 hashCode 与 equals 方法。
项类持有一个 BigInteger 对象(项的系数)和一个指数类对象。项类配备求导方法,返回一个项表。
表达式类持有一个 HashMap 对象,以指数类对象为键,以持有此指数类对象的项类对象为值,实现读入项合并。表达式类配备求导方法,返回一个表达式。
第二次作业读入处理:根据加减运算符分割表达式为各个项,在项内使用正则表达式提取各个因子。
类图:
代码行数:
方法复杂度:
本次作业存在化简问题,限于个人能力,我在实现化简时使用了较多分支结构,没有遵循高内聚低耦合的原则,使得方法复杂度见红。
第三次作业
第三次作业涉及因子嵌套,根据表达式由项构成,项由因子构成,因子嵌套因子的描述,可抽象出三个类——表达式、项、因子。
由于多种因子的存在,这里的因子类表现为一个接口。为了实现表达式的求导以及化简,接口内的方法定义为求导、合并、裂项、展开、提公因式等。表达式也是一个因子。
项类持有一个 BigInteger 对象(项的系数)和一个因子表对象。项类配备求导方法,返回一个项表。
表达式因子类持有一个项表。
第三次作业读入处理:采取状态机的解析模式,一趟扫描完成各个对象的创建,可在读入时完成去除冗余括号、三角函数特殊函数值代换、合并同类项等工作。
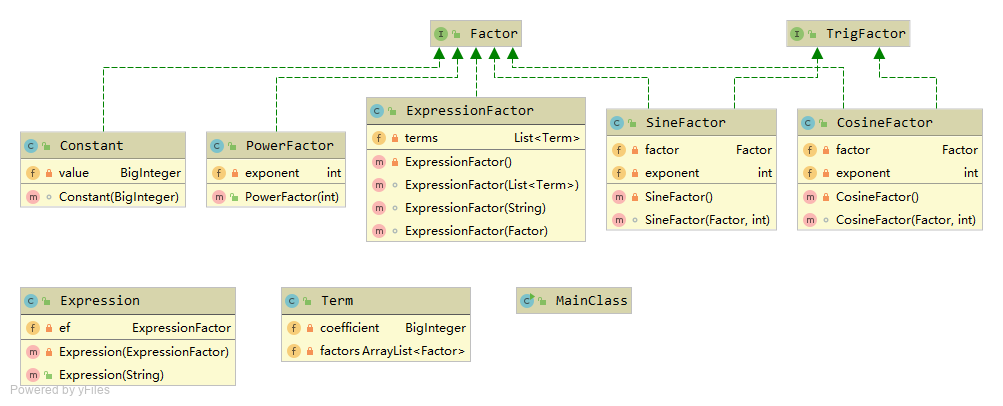
类图:
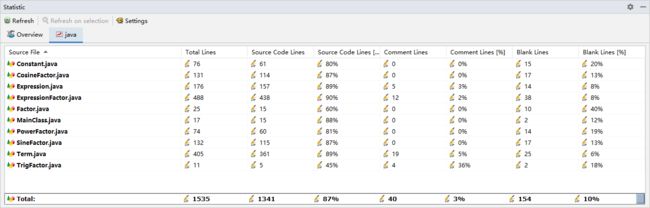
代码行数:
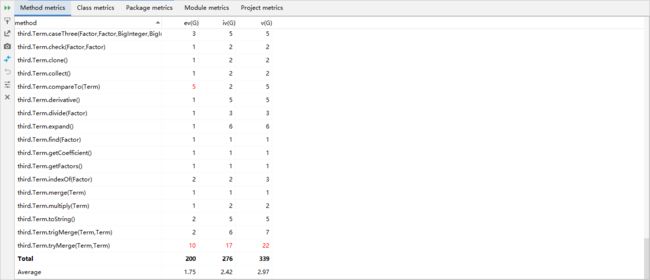
方法复杂度:
第三次作业较为复杂,为了实现求导以及求导后的化简,我一共写了114个方法,限于个人能力,其中与化简相关的部分方法具有超高的复杂度(全红)。
程序bug
三次作业在中强测中均未被发现bug,仅第二次作业在互测中被发现1处bug,源于写代码时的一个小疏忽。
发现他人程序bug的策略
我测试他人程序的流程分三步。
第一步使用对拍器测试他人的程序。
第二步测试边界,例如逐渐增加第三次作业中表达式括号嵌套层数。
第三步尝试阅读他人程序复杂度较高的部分,例如格式检查部分,进行针对性测试。不过,鉴于大家的编程风格差异较大,读懂他人代码并不是一件容易的事。
应用对象创建模式来重构
可应用工厂模式来降低创建对象的复杂度,同时便于扩展。
心得体会
评判一个程序的好坏有多个评判标准,应该学会综合考量,设计出较好的程序架构。
在迭代式开发的开发过程中,需要合理预测未来需求,预留需求接口,但出现实现需求不匹配时,应该大胆重构。