【深度强化学习】A3C

上一篇对Actor-Critic算法的学习，了解Actor-Critic的流程，但由于普通的Actor-Critic难以收敛，需要一些其他的优化。而Asynchronous Advantage Actor-Critic（A3C）就是其中较好的优化算法。

A3C Introduction

为了打破数据之间的相关性，DQN和DDPG的方法都利用了经验回放的技巧。然而，打破数据的相关性，经验回放并非是唯一的方法。另外一种方法是异步的方法。比如，学习下棋，总是和同一个人下，期望提高棋艺，但到一定程度就难以提高了，此时最好的方法就是另寻高手切磋。
A3C的思路也是如此，它利用多线程的方法，同时在多个线程里面分别与环境进行交互学习，每个线程都把学习的成果汇总起来，整理保存在一个公共的地方。并且，定期从公共的地方把大家的齐心学习的成果拿回来，指导自己和环境后面的学习交互。
这样，A3C避免了经验回放相关性过强的问题，同时做到了异步并发的学习模型。

A3C的算法优化

相比Actor-Critic，A3C的优化主要有3点，分别是异步训练框架，网络结构优化，Critic评估点的优化。其中异步训练框架是最大的优化。

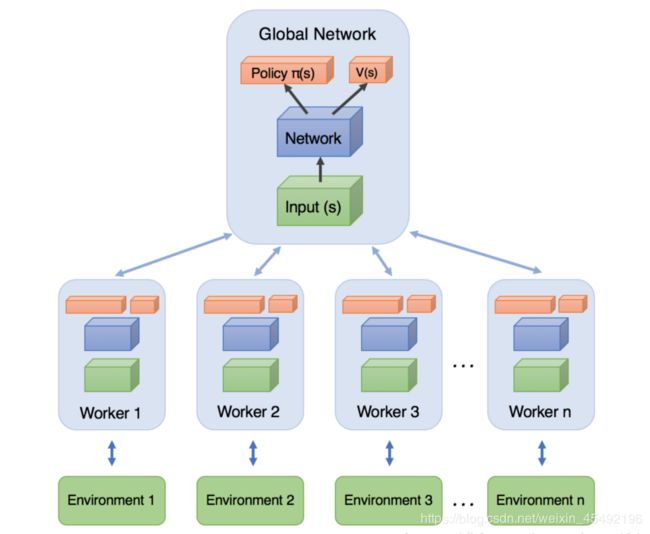
1. 首先来看这个异步训练框架：

• Global Network就是上一节说的共享的公共部分，主要是一个公共的神经网络模型，这个神经网络包括Actor网络和Critic网络两部分的功能。
• 下面有n个worker线程，每个线程里有和公共的神经网络一样的网络结构，每个线程会独立的和环境进行交互得到经验数据，这些线程之间互不干扰，独立运行。
• 每个线程和环境交互到一定量的数据后，就计算自己线程里的神经网络损失函数的梯度，但是这些梯度并不更新自己线程里的神经网络，而是去更新公共的神经网络。也就是n个线程会独立的使用累积的梯度分别更新公共部分的神经网络模型参数。
• 每隔一段时间，线程会将自己的神经网络的参数更新为公共神经网络的参数，进而指导后面的环境交互。

可见，公共部分的网络模型就是我们要学习的模型，而线程里的网络模型主要是用于和环境交互使用的，这些线程里的模型可以帮助线程更好的和环境交互，拿到高质量的数据帮助模型更快收敛。

2. 第二个优化：网络结构的优化

• 在Actor-Critic中，使用了两个不同的网络Actor和Critic。
• 在A3C中，把两个网络放到了一起，即输入状态$S$，输出状态价值$V$，和对应的策略$\pi$。当然，我们仍可以把Actor和Critic看作独立的两块，分别处理，如下图：
  

3. Critic评估点的优化

• 在Actor-Critic算法中，讨论了不同的Critic评估点的选择，其中优势函数$A$作为Critic评估点，优势函数$A$在时刻$t$不考虑参数的默认表达式：
  $$A\left(S,A,t\right)=Q\left(S,A\right)-V\left(S\right)$$
  $Q\left(S,A\right)$的值一般可以通过单步采样近似估计，即：
  $$Q\left(S,A\right)=R+\gamma V\left(S^{\prime }\right)$$
  这样优势函数去掉动作可表达为：

$$A\left(S,t\right)=R+\gamma V\left(S^{\prime }\right)-V\left(S\right)$$

其中$V\left(S\right)$的值通过Critic网络来学习得到。

在A3C中，采样更进一步，使用了N步采样，以加速收敛。则A3C中的优势函数表达为：
$$A\left(S,t\right)=R_t+\gamma R_{t+1}+\cdots +{\gamma }^{n-1}{R}_{t+n-1}+{\gamma }^{n}V(S^{\prime })-V(S)$$

对于Actor和Critic的损失函数部分，和Actor-Critic基本相同。有一个小的优化点就是在Actor-Critic策略函数的损失函数中，加入了策略π的熵项,系数为c, 即策略参数的梯度更新和Actor-Critic相比变成了这样：
$$\theta =\theta +\alpha {▽}_{\theta }\log {\pi }_{\theta }\left(s_t,a_t\right)A\left(S,t\right)+c{▽}_{\theta }H(\pi (S_t,\theta ))$$

A3C算法流程

由于A3C是异步多线程的，这里给出任意一个线程的算法流程。

输入： 公共部分的A3C神经网络结构，对应参数$\theta$，$w$，本线程的A3C神经网络结构，对应参数${\theta }^{\prime }$，$w^{\prime }$，全局共享的迭代轮数$T$，全局最大迭代次数$T_{max}$，线程内单次迭代时间序列最大长度$T_{local}$，状态特征维度$n$，动作集$A$，步长$\alpha$，$\beta$，熵系数$c$，衰减因子$\gamma$
输出： 公共部分的A3C神经网络参数$\theta$，$w$

1. 更新时间序列$t=1$
2. 重置Actor和Critic的梯度更新量：$d\theta \leftarrow 0,dw\leftarrow 0$
3. 从公共部分的A3C神经网络同步参数到本线程的神经网络：${\theta }^{\prime }=\theta$，$w^{\prime }=w$
4. $t_{start}=t$，初始化状态$s_t$
5. 基于策略$\pi (a_t\mid s_t;\theta )$选择动作$a_t$
6. 执行动作$a_t$得到奖励$r_t$和新状态$s_{t+1}$
7. $t\leftarrow t+1,T\leftarrow T+1$
8. 如果$s_t$是终止状态，或$t-t_{start}==t_{local}$，则进入步骤9，否则回到步骤5
9. 计算最后一个时间序列位置$s_t$的$Q(s,t)$:
$$Q(s,t)=\{\begin{array}{ll}0& terminalstate\\ V(s_t,w^{\prime })& noneterminalstate,bootstrapping\end{array}$$
10. for $i\in (t-1,t-2,\dots ,t_{start})$
　　a) 计算每个时刻的$Q(s,i)$：$Q(s,i)=r_i+\gamma Q(s,i+1)$
　　b) 累计Actor的本地梯度更新：

$$d\theta =d\theta +{▽}_{{\theta }^{\prime }}\log {\pi }_{{\theta }^{\prime }}\left(s_i,a_i\right)(Q\left(s,i\right)-V(S_i,w^{\prime }))+c{▽}_{{\theta }^{\prime }}H(\pi (s_i,{\theta }^{\prime }))$$
　　c) 累计Critic的本地梯度更新：

$$dw\leftarrow dw+\frac{\partial (Q(s,i)-V(S_i,w^{\prime }){)}^2}{\partial w^{\prime }}$$

11. 更新全局神经网络的模型参数：

$$\theta =\theta -\alpha d\theta ,w=w-\beta dw$$

12. 如果$T>T_{max}$，则算法结束，输出公共部分的A3C神经网络参数$\theta$，$w$，否则进入步骤3

---

笔记参考刘建平Pinard博客