谈谈Processing 3D世界 一
Processing起初给人的映像是处理2D的一款优秀的软件。但其实抛开引用OpenGL不说,它也有一套完备的处理3D的方法。
我们知道旋转的函数是:rotate() 。
当然,这个函数目前也能满足我们的需求,但我们现在已经是3D了对吧?
在2D世界中我们要么 顺时针旋转 ,要么 逆时针旋转 。再倒腾不出什么花样。
然而在3D世界中旋转,我们需要一个 角 (angle)和一个 旋转轴 (Rotation Axis)。
物体会沿着给定的旋转轴旋转特定的角度。
咱们可以通过依次围绕 x轴、y轴、z轴来进行顺时针旋转或逆时针旋转,
从而使被旋转的物件能转动到任何角度的姿态,这称为—— 欧拉角 (Euler angles)。
*顺时针旋转为正,逆时针旋转为负。
--- 深入 ---
讲到欧拉角一般会提到万向节锁死(Gimbal Lock),有兴趣的同学可以看看延展视频:
史上最清白的万向节锁死讲解!
--- 深入 ---
好,我们来看看函数:
rotateX(angle)
rotateY(angle)
rotateZ(angle)
函数很简单,不过如果你傻乎乎的填入一个角度,函数却并不会友好的对待你。
因为这里的角度是一个 弧度 ,写代码的都喜欢折磨玩。
angle的值应该是:0 - 2PI之间,对应的便是0 - 360度。
我们可以用度转弧函数来转换一下,比如这样:
float angle = radians(45);
rotateZ(angle);
你可以自己动手尝试一下旋转各个轴。
..
.
.
.
.
怎么样?是不是觉得很别扭,有点找不着北?
我们可以打开Processing的帮助文档,看看官方的例子:

官方案例,有两处值得我们注意。
1. 使用了translate()。
2. 设置rect(矩形)的两个顶点,一个为负,一个为正。
这是为什么呢?
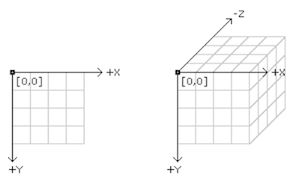
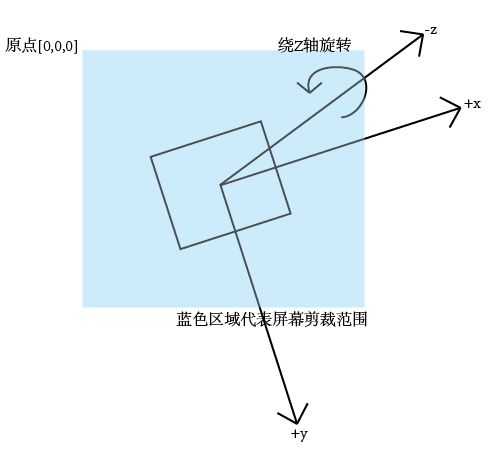
还记得我们之前说过的 Processing的3D空间坐标方向 吗?我们来再次回顾一下:
Processing的坐标 原点 ( origin )是位于窗口左上角,并贴合屏幕的。我们在屏幕中绘制一个图形,便是处在这个坐标系下。
如果我们绕x轴转动,转动的对象将是整个画面。这是因为,我们转动的是 世界坐标系 。
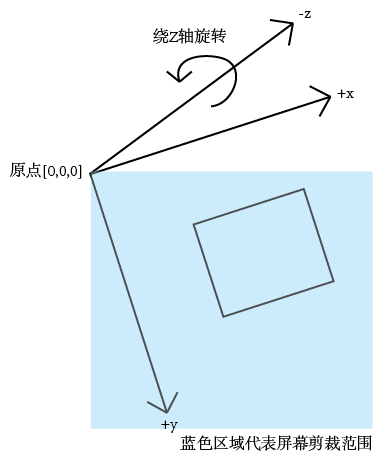
因为图形围绕原点做了一个很大的圆周运动,十分容易脱离屏幕。通常情况下,我们会比较喜欢图像绕屏幕中心旋转,对吧?
倘若我们将物体绘制在原点附近,使其中心点与原点重合,比如这样:
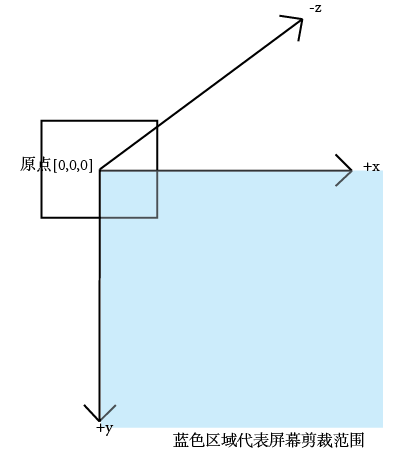
如果要这样设计,我必然会定义一些包含负数的顶点。
然后我们再次旋转画面:
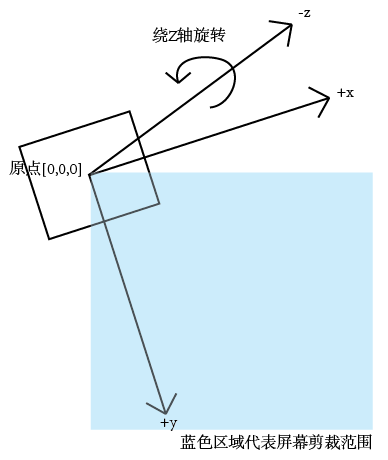
现在是不是好多了?图形没有乱跑,开始自旋了。
但是这样,会使我们看不见完整的图形。毕竟,我们希望图形能显示在屏幕中,
所以我们平移坐标系到屏幕中央,完成这个神圣任务的就是:
translate(width/2, height/2, 0.0) // 平移矩阵
相当不错!是吗?
现在我们可以根据上面的例子,动手来修改一下我们小小的三角形。有疑惑的同学,可以查看最开始的例子。
有兴趣的朋友可以一起来研究研究。好,前言少叙。我们直接开始正题:
3D编程世界的hello world
Java 代码,双击复制代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
// 绘制三角形
// 属性
PVector[] vec;
// 顶点-位置
PVector offset;
// 坐标系偏移量
color[] cs;
// 色表
final
int
EDGE =
3
;
// 多边形边数
void
setup() {
// 设置窗口,一句话就搞定了T_T
size(
400
,
400
, P3D);
// 关闭描边
noStroke();
// 给顶点赋值
vec =
new
PVector[EDGE];
for
(
int
i =
0
; i < vec.length; i++) {
vec = CalculatePointOfTheCircle(
float
(i) * (
360.0
/
float
(vec.length)));
}
// 给色表赋值
cs =
new
color[
3
];
cs[
0
] = color(
255
,
0
,
0
);
cs[
1
] = color(
0
,
255
,
0
);
cs[
2
] = color(
0
,
0
,
255
);
// 设置偏移
offset =
new
PVector(
0.5
*width,
0.5
*height,
0.0
);
}
void
draw() {
// 清除屏幕缓冲区
background(
0
);
// 变换矩阵
translate(offset.x, offset.y, offset.z);
float
angle = radians(frameCount%
360
);
rotateZ(angle);
// 旋转的是世界坐标
// 绘制图形
beginShape();
for
(
int
i =
0
; i < vec.length; i++) {
fill(cs[i%cs.length]);
vertex(vec.x, vec.y, vec.z);
}
endShape(CLOSE);
}
// 求取点在圆中对应角度的位置
// 无论是三角形、正方形、还是六菱形,它们都能在圆中找到对应的点
// 圆心就在坐标系原点上
PVector CalculatePointOfTheCircle(
float
angle) {
float
size =
100.0
;
// 多边形的尺寸
float
x = sin(radians(angle)) * size;
float
y = cos(radians(angle)) * size;
PVector v =
new
PVector(x, y,
0.0
);
return
v;
}
|
---------------------这里是华丽的分割线-------------------------
绘制多边形
有的同学可能会开始晕了,一个hello world要不要这么复杂?这不Processing呀!
嗯,是的。让我们把这个hello world“标准化”一下:
Java 代码,双击复制代码
|
1
2
3
4
5
|
beginShape();
vertex(
50
,
20
);
vertex(
85
,
75
);
vertex(
15
,
75
);
endShape(CLOSE);
|
现在我们把代码成功缩减到了5行==!。
它运行的效果是这样
这里我们认识两个概念:顶点& 形状
beginShape()、endShape(CLOSE)这对基友负责绘制形状,表示绘制工作的开始和结束。
在图形学中,我们通常将这些形状称作多边形。
而在计算机中,我们用于描述形状(多边形)的方法就是‘顶点’了。
理科的盖,知道离散数学,文科的盖知道点线面。这里就不废话了。
vertex()描述的是顶点的位置(position),但我们可以看到函数中值填入了2个值。
因此目前这个三角形还只是一个2D空间中的图形,啊,被骗了!
好像绕回原点了,不过没关系,想要3D化也十分简单。这可是我大Processing!
我们向函数中多填入一个值便可以:
vertex(x, y, z); // 这样便能描述3D空间中的任意位置了。
比如这样:
vertex(50, 20, 0);
让我们来看看Processing的3D空间坐标方向,帮助找找这个点的位置:
根据上图,我们知道这个点仍然是贴合在屏幕上的,既不远去,也不后退。
那么我们这样修改程序后是否能运行呢?——你可以试试。
既然我们将空间描述成3D了,那么我们就必须对Processing指定3D渲染器。
这在设置窗口的时候一并完成了:
size(100,100, P3D); // 我们使用P3D这个渲染器
那么我们更新代码:
Java 代码,双击复制代码
|
1
2
3
4
5
6
7
|
size(
100
,
100
, P3D);
beginShape();
vertex(
50
,
20
,
0
);
vertex(
85
,
75
,
0
);
vertex(
15
,
75
,
0
);
endShape(CLOSE);
|
运行成功!
但是看起来和之前没卵区别?你可以试着改改z值。
---------------------这里是华丽的分割线-------------------------
给图形着色
恩,现在我们要有一点追求,这个三角形并没有颜色!
在我大Processing中任何着色的方法都一样,那就是:
fill() // 填充颜色
noFill() // 不填充颜色
stroke() // 线框颜色
noStroke() // 不给线框上色(没线框)
我们可以试着把程序改一下:
Java 代码,双击复制代码
|
1
2
3
4
5
6
7
8
9
10
|
size(
400
,
400
, P3D);
noStroke();
fill(
0
,
255
,
0
);
beginShape();
vertex(
200
,
100
,
0
);
vertex(
300
,
300
,
0
);
vertex(
100
,
300
,
0
);
endShape(CLOSE);
|
恩,现在似乎变得华丽了一点...我们可以想象它是一块绿宝石...好吧,我承认单调了一点。
如何能有咱们开始时那样的混合过渡的色彩呢?
方法是,我们可以为每个顶点定义一次色彩,我大Processing就是怎么霸气:
Java 代码,双击复制代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
// 设定窗口
size(
400
,
400
, P3D);
// 清除背景(图像缓冲区)
background(
0
);
// 设定图像显示参数
noStroke();
// 绘制图形
beginShape();
fill(
255
,
0
,
0
);
// 设定顶点颜色
vertex(
200
,
100
,
0
);
fill(
0
,
255
,
0
);
// 系统会自动为两个顶点做插值计算
vertex(
300
,
300
,
0
);
fill(
0
,
0
,
255
);
vertex(
100
,
300
,
0
);
endShape(CLOSE);
|
---------------------这里是华丽的分割线-------------------------
图形变换
现在感觉已经相当不错~,咱们乘势追击,来说说旋转。
当然,这个函数目前也能满足我们的需求,但我们现在已经是3D了对吧?
在2D世界中我们要么 顺时针旋转 ,要么 逆时针旋转 。再倒腾不出什么花样。
然而在3D世界中旋转,我们需要一个 角 (angle)和一个 旋转轴 (Rotation Axis)。
物体会沿着给定的旋转轴旋转特定的角度。
咱们可以通过依次围绕 x轴、y轴、z轴来进行顺时针旋转或逆时针旋转,
从而使被旋转的物件能转动到任何角度的姿态,这称为—— 欧拉角 (Euler angles)。
*顺时针旋转为正,逆时针旋转为负。
--- 深入 ---
讲到欧拉角一般会提到万向节锁死(Gimbal Lock),有兴趣的同学可以看看延展视频:
史上最清白的万向节锁死讲解!
--- 深入 ---
好,我们来看看函数:
rotateX(angle)
rotateY(angle)
rotateZ(angle)
函数很简单,不过如果你傻乎乎的填入一个角度,函数却并不会友好的对待你。
因为这里的角度是一个 弧度 ,写代码的都喜欢折磨玩。
angle的值应该是:0 - 2PI之间,对应的便是0 - 360度。
我们可以用度转弧函数来转换一下,比如这样:
float angle = radians(45);
rotateZ(angle);
你可以自己动手尝试一下旋转各个轴。
..
.
.
.
.
怎么样?是不是觉得很别扭,有点找不着北?
我们可以打开Processing的帮助文档,看看官方的例子:

官方案例,有两处值得我们注意。
1. 使用了translate()。
2. 设置rect(矩形)的两个顶点,一个为负,一个为正。
这是为什么呢?
还记得我们之前说过的 Processing的3D空间坐标方向 吗?我们来再次回顾一下:
Processing的坐标 原点 ( origin )是位于窗口左上角,并贴合屏幕的。我们在屏幕中绘制一个图形,便是处在这个坐标系下。
如果我们绕x轴转动,转动的对象将是整个画面。这是因为,我们转动的是 世界坐标系 。

因为图形围绕原点做了一个很大的圆周运动,十分容易脱离屏幕。通常情况下,我们会比较喜欢图像绕屏幕中心旋转,对吧?
倘若我们将物体绘制在原点附近,使其中心点与原点重合,比如这样:

如果要这样设计,我必然会定义一些包含负数的顶点。
然后我们再次旋转画面:

现在是不是好多了?图形没有乱跑,开始自旋了。
但是这样,会使我们看不见完整的图形。毕竟,我们希望图形能显示在屏幕中,
所以我们平移坐标系到屏幕中央,完成这个神圣任务的就是:
translate(width/2, height/2, 0.0) // 平移矩阵

相当不错!是吗?
现在我们可以根据上面的例子,动手来修改一下我们小小的三角形。有疑惑的同学,可以查看最开始的例子。