数据挖掘学习（二）——数据探索与清洗

笔者是一个痴迷于挖掘数据中的价值的学习人，希望在平日的工作学习中，挖掘数据的价值，找寻数据的秘密，笔者认为，数据的价值不仅仅只体现在企业中，个人也可以体会到数据的魅力，用技术力量探索行为密码，让大数据助跑每一个人，欢迎直筒们关注我的公众号，大家一起讨论数据中的那些有趣的事情。

我的公众号为：livandata

1、数据探索与数据清洗概述：

淘宝零食类数据为分析案例：

如何发现空值、异常值等。

#!/usr/bin/env python
# _*_ UTF-8 _*_

import matplotlib.pylab as pyl
import numpy as npy
import pandas as pda
import pymysql

# 导入数据：
conn = pymysql.connect(host='127.0.0.1',
                       user='root',
                       passwd='123456',
                       db='livan')

sql = "select * from taob"

data = pda.read_sql(sql, conn)

print(data.describe())
# 数据清洗：
# 1、首先把价格为零的数据变为空值（插补法）：
x=0
data["price"][(data["price"]==0)]= None
for i in data.columns:
    for j in range(len(data)):
        if(data[i].isnull())[j]:
            data[i][j]="36"
            x+=1
print(x)

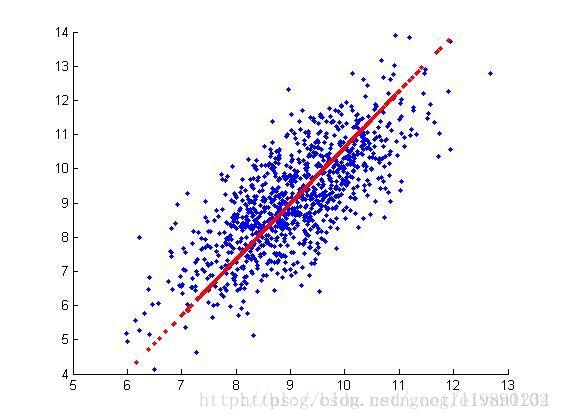
# 2、异常值处理：
# 画散点图（横轴为价格，纵轴为评论数）
# 得到价格
data2 = data.T
price = data2.values[2]
# 得到评论数：
comt = data2.values[3]
pyl.plot(price, comt, 'o')
pyl.show()
# 异常值处理
# 评论数异常为>200000；价格异常为>2300；
line = len(data.values)
col = len(data.values)
da = data.values
for i in range(0, line):
    for i in range(0, col):
        if(da[i][2]>2300):
            da[i][2] = "36"
        if(da[i][3]>"200000"):
            da[i][j] = "58"

# 查看修正后的数据：
da2 = da.T
price = da2[2]
comt = da2[3]
pyl.plot(price, comt, 'o')
pyl.show()

2、数据分布探索实战：

数据清洗，数据分布式探索，一方面从大范围往小处看你，另一方面从小范围往大处看。探索玩整体趋势后再去探索局部的区域。

#!/usr/bin/env python
# _*_ UTF-8 _*_

import matplotlib.pylab as pyl
import numpy as npy
import pandas as pda
import pymysql

# 导入数据：
conn = pymysql.connect(host='127.0.0.1',
                       user='root',
                       passwd='123456',
                       db='livan')

sql = "select * from taob"

data = pda.read_sql(sql, conn)

print(data.describe())
# 数据清洗：
# 1、首先把价格为零的数据变为空值（插补法）：
x=0
data["price"][(data["price"]==0)]= None
for i in data.columns:
    for j in range(len(data)):
        if(data[i].isnull())[j]:
            data[i][j]="36"
            x+=1
print(x)

# 2、异常值处理：
# 画散点图（横轴为价格，纵轴为评论数）
# 得到价格
data2 = data.T
price = data2.values[2]
# 得到评论数：
comt = data2.values[3]
pyl.plot(price, comt, 'o')
pyl.show()

# 异常值处理
# 评论数异常为>200000；价格异常为>2300；
line = len(data.values)
col = len(data.values)
da = data.values
for i in range(0, line):
    for i in range(0, col):
        if(int(da[i][2])>200):
            da[i][2] = "36"
        if(float(da[i][3])>10000):
            da[i][3] = "58"

# 查看修正后的数据：
da2 = da.T
price = da2[2]
comt = da2[3]
pyl.plot(price, comt, 'o')
pyl.show()

# 分布分析：
# 极差：最大值-最小值；
# 组距：极差/组数；
pricemax = float(da2[2]).max()
pricemin = float(da2[2]).min()
commentmax = float(da2[3]).max()
commentmin = float(da2[3]).min()

pricerg = pricemax-pricemin
commentrg = commentmax - commentmin

pricedst = pricerg/12
commentdst = commentrg/12

# 画价格的直方图：
pricesty = npy.arange(pricemin, pricemax, pricedst)
pyl.hist(da2[2], pricesty)
pyl.show()

# 画评论的直方图：
commentsty = npy.arange(commentmin, commentmax, commentdst)
pyl.hist(da2[3],commentsty)
pyl.show()

数据集成的实战：

#!/usr/bin/env python
# _*_ UTF-8 _*_

import matplotlib.pylab as pyl
import numpy as npy
import pandas as pda
import pymysql

a = npy.array([[1,5,6],[9,4,3]])

b = npy.array([[6,36,7],[2,3,39]])

# 数据整合：
c = npy.concatenate((a, b))
print(c)

3、数据变换：

离差：最大值与最小值之间的差；可以消除量纲（即单位）的影响。

#!/usr/bin/env python
# _*_ UTF-8 _*_

import matplotlib.pylab as pyl
import numpy as npy
import pandas as pda
import pymysql

conn = pymysql.connect(host='127.0.0.1',
                       user='root',
                       passwd='123456',
                       db='livan')

sql = "select price, comments from taob"

data = pda.read_sql(sql, conn)

# print(data.describe())
#
# # 计算离差标准化：可以消除量纲，消除单位的影响：
# 又被称作：最小-最大标准化。
#
# data2 = (data-data.min())/(data.max()-data.min())
#
# print(data2)

# 标准差标准化：消除量纲等因素影响，同时也可以消除自身数据变异的影响。
# 特性为：平均数为零，标准差为1.
# 又被称作：零-均值标准化

data3 = (data-data.mean())/(data.std())

print(data3)

# 小数定标规范化：消除单位影响。
# 消除量纲（单位）的影响。
# ceil（）即进一取整。

k = npy.ceil(npy.log10(data.abs().max()))

data4 = data/10**(k)

离散化：将一些连续的数据离散化。

等宽离散化：将值放在固定宽度的区间。

等频率离散化：将相同数量的点放在每个区间里面。

一维聚类离散化：

#!/usr/bin/env python

# _*_ UTF-8 _*_

import matplotlib.pylab as pyl
import numpy as npy
import pandas as pda
import pymysql

conn = pymysql.connect(host='127.0.0.1',
                       user='root',
                       passwd='123456',
                       db='livan')

sql = "select price, comments from taob"

data = pda.read_sql(sql, conn)

data5 = data[u"price"].copy()

data6 = data5.T

data7 = data6.values

print(data7)

k = 3

# abc = [1, 5, 7, 8, 10]
#
# # 离散化处理：cut(需要划分的数据, 划分的区间<等分的份数>，标签<每一份代表什么>)
# # 等宽离散化：
# pda.cut(abc, 4, labels=["便宜", "适中", "有点贵", "天价"])
#
# # 非等宽离散化：
# pda.cut(abc, [3, 6, 10, 19], labels=["便宜", "适中", "有点贵"])

c1 = pda.cut(data7, k, labels=["便宜", "适中", "有点贵"])

print(c1)

c2 = pda.cut(data7,
             [0, 50, 100, 300, 500, 2000, data7.max()],
             labels=["非常便宜", "便宜", "适中", "有点贵", "很贵", "非常贵"])

print(c2)

4、属性构造：

#!/usr/bin/env python

# _*_ UTF-8 _*_

import matplotlib.pylab as pyl
import numpy as npy
import pandas as pda
import pymysql

conn = pymysql.connect(host='127.0.0.1',
                       user='root',
                       passwd='123456',
                       db='livan')

sql = "select * from myhexun"

data = pda.read_sql(sql, conn)

ch = data[u"comment"]/data[u"hits"]
# 通过属性之间的关系构造新的属性
data[u"评点比"] = ch

file = "./hexun.xls"
# 将评点比写在Excel中。
data.to_excel(file, index=False)

print(ch)

5、数据规约（即对数据进行精简）：

属性规约：对属性进行精简，主成分分析等；

数值规约：对重复数值等进行精简，以方便处理，离散化处理可以简单的划分为数值规约。

1）数据降维

    对于现在维数比较多的数据，我们首先需要做的就是对其进行降维操作。降维，简单来说就是说在尽量保证数据本质的前提下将数据中的维数降低。降维的操作可以理解为一种映射关系，例如函数 ，即由原来的二维转换成了一维。处理降维的技术有很多种，如前面的SVD奇异值分解，主成分分析(PCA)，因子分析(FA)，独立成分分析(ICA)等等。

2）PCA的概念

    PCA是一种较为常用的降维技术，PCA的思想是将 维特征映射到 维上，这 维是全新的正交特征。这 维特征称为主元，是重新构造出来的 维特征。在PCA中，数据从原来的坐标系转换到新的坐标系下，新的坐标系的选择与数据本身是密切相关的。其中，第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选取的是与第一个坐标轴正交且具有最大方差的方向，依次类推，我们可以取到这样的 个坐标轴。

3）PCA的操作过程

    3.1）PCA的操作流程大致如下：

去平均值，即每一位特征减去各自的平均值

计算协方差矩阵

计算协方差矩阵的特征值与特征向量

对特征值从大到小排序

保留最大的 个特征向量

将数据转换到 个特征向量构建的新空间中

    3.2）具体的例子

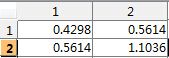
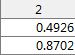
假设二维数据为：

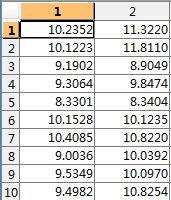
取平均值：我们计算每一维特征的平均值，并去除平均值，我们计算出均值为：

去除均值后的矩阵为：

计算的协方差矩阵：

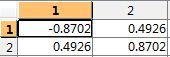
计算的特征值与特征向量

其中，特征值为

特征向量为

对特征值进行排序，显然就两个特征值

选择最大的那个特征值对应的特征向量：

转换到新的空间：

3.3）实验的仿真：

我们队一个数据集进行了测试：

#!/usr/bin/env python

# _*_ UTF-8 _*_

import matplotlib.pylab as pyl
import numpy as npy
import pandas as pda
import pymysql
from sklearn.decomposition import PCA

# 主成分分析：
conn = pymysql.connect(host='127.0.0.1',
                       user='root',
                       passwd='123456',
                       db='livan')

sql = "select hits, comment from myhexun"

data = pda.read_sql(sql, conn)

ch = data[u"comment"]/data[u"hits"]

data[u"hits"] = ch
# 主成分分析进行中：
pca1 = PCA()

pca1.fit(data)
#返回模型中的各个特征量：
characteristic = pca1.components_

print(characteristic)

# 返回各个成分中各自方差的百分比，贡献率：
rate = pca1.explained_variance_ratio_

print(rate)

# 降维操作：
# pca中的参数为希望的维数：
pca2 = PCA(2)

pca2.fit(data)

reduction = pca2.transform(data)

characteristic2 = pca2.components_

print(characteristic2)

print(reduction)

# 对降维数据进行恢复：
recovery = pca2.inverse_transform(reduction)

print(recovery)