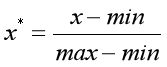R语言学习（三）— 数据预处理

 

第四章—数据预处理

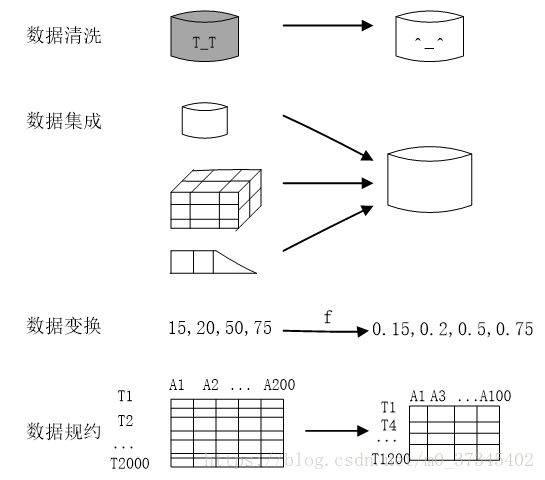
4.1数据清洗

1.缺失值处理

2.异常值处理

4.2数据集成

1.实体识别

2.冗余属性识别

4.3 数据变换

1.简单函数变换

2.规范化

3.连续属性离散化

4.属性构造

4.4数据规约

1.属性规约——属性子集选择

2.属性规约——维度规约

3.数值规约

4.参数回归

---

第四章—数据预处理

目的

• 提高数据质量。
• 让数据更好的适应特定的分析技术或模型。

常见的步骤

4.1数据清洗

1.缺失值处理

• 删除法

     na.omit()：移除所有含有缺失数据的行。

     思考？列删除如何删：删除data的第p列，如何删除。

• 替换法

     数值型变量：均值替换

     非数值型变量：观测值的中位数替换。

• 插补法

     回归插补法

#读取销售数据文件，提取标题行
inputfile=read.csv(file = "catering_sale.csv",header = T)
#变换变量名
inputfile=data.frame(sales=inputfile$'销量',date=inputfile$'日期')
#数据截取
inputfile=inputfile[5:16,]
#缺失数据的识别
is.na(inputfile)    #判断是否存在缺失
n=sum(is.na(inputfile))    #输出缺失值个数

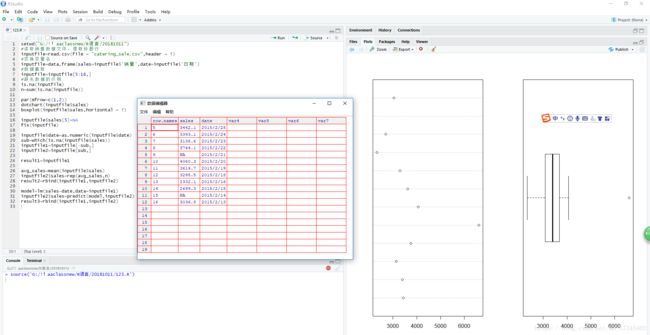
#异常值识别
par(mfrow=c(1,2))    #将绘图窗口华为一行两列，同时显示两图
dotchart(inputfile$sales)    #绘制变量散点图
boxplot(inputfile$sales,horizontal = T)    #绘制水平箱形图

#异常数据处理
inputfile$sales[5]=NA    #将异常值处理为缺失值
fix(inputfile)     #表格形式呈现数据

#缺失值的处理
inputfile$date=as.numeric(inputfile$date)    #将日期转换成数值型变量
sub=which(is.na(inputfile$sales))    #识别缺失值所在行数
inputfile1=inputfile[-sub,]    #将数据集分为完整数据和缺失数据两部分
inputfile2=inputfile[sub,]

#行删除法处理缺失，结果转存
result1=inputfile1

#均值替换法处理缺失，结果转存
avg_sales=mean(inputfile$sales)    #求变量未缺失部分的均值
inputfile2$sales=rep(avg_sales,n)    #用均值替换缺失
result2=rbind(inputfile1,inputfile2)    #并入完成插补的数据

#回归插补法处理缺失，结果转存
model=lm(sales~date,data=inputfile1)    #回归模型拟合
inputfile2$sales=predict(model,inputfile2)    #模型预测
result3=rbind(inputfile1,inputfile2)

2.异常值处理

【注】不处理：是在分析之后发现异常值也是正确的情况下，比如小概率事件确实发生了，则不处理。

4.2数据集成

数据集成

将多个数据源合并存放在一个一致的数据存储中的过程。

多个数据框合并到一个数据框的过程。

常用函数merge()

• merge(数据框1，数据框2，by=“关键字”)
• 以关键字为依据，以行为单位做列属性补齐方式合并两个数据框。
• 合并后的新数据框，自动按关键字取值大小升序排列各行。

      在df1中关键字列中按元素依次往下去比对df2中相同关键字的列的元素，具有相同值得会被元素所在两行会合并到新生成的数据框中。

• 【注】在关键字指定的属性中，只有在两个数据框中共有的实例才会出现在新数据框中。
• merge(df1,df2,by.x=“keyword1”,by.y=“keyword2”)

      用于标示出两个数据框里含有相同信息但名称不同的两个变量。

> kids<-c("Jack","Jill","Jillian","John")
> states<-c("CA","MA","MA","HI")
> d1<-data.frame(kids,states)
> d1
>
> ages<-c(10,7,12)
> kids<-c("Jill","Lillian","Jack")
> d2<-data.frame(ages,kids)
> d2
>
> d<-merge(d1,d2)
> d
>
> ages<-c(12,10,7)
> pals<-c("Jack","Jill","Lillian")
> d3<-data.frame(ages,pals)
> d3
>
> merge(d1,d3,by.x = "kids",by.y = "pals")

 

1.实体识别

解决不同数据源不一致的问题：命名不一致、单位不一致等。

同名异义：数据源A中的属性ID和数据源B中的属性ID分别描述的是客户编号和订单编号，即描述的是不同的实体。

异名同义：数据源A中的sales_dt和数据源B中的sales_date都是是描述销售日期的，即A. sales_dt= B. sales_date。

单位不统一：描述同一个实体分别用的是国际单位和中国传统的计量单位。

2.冗余属性识别

相同属性：当做完实体识别后，相同的属性就容易识别。

相关属性：给定两个数值型的属性A和B，根据其属性值，可以用相关系数度量一个属性在多大程度上蕴含另一个属性。

4.3 数据变换

1.简单函数变换

• 将原始数据进行数学函数变换。
• 作用：

        将不具正态分布的随机变量变换成具正态分布的随机变量。

        时序数据中：差分运算等将非稳定型序列变换成稳定序列。

        取值范围太大：对数变换进行压缩。

2.规范化

• 将数据按一定规律进行缩放，使其落入一个特定区域；一般映射到[-1,1]或[0,1]内。
• 最小最大规范化：线性变换到[0,1]

       缺点：数据若不均匀，则易造成所有的数据很靠近0。如max，min值为错误数据。

       将来若取值若超过[min,max]范围，会出错。

 

 

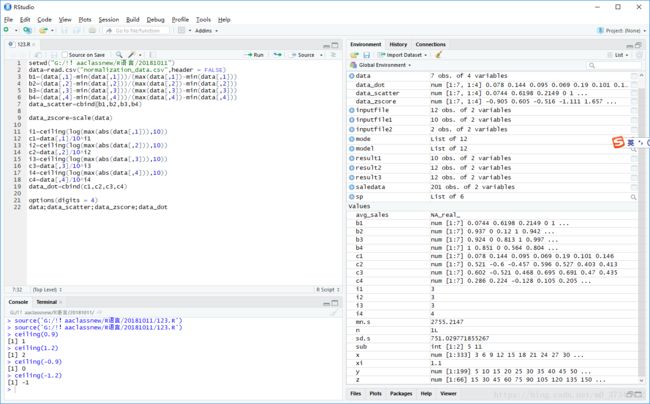
setwd("G:/!！aaclassnew/R语言/20181011")
data=read.csv("normalization_data.csv",header = FALSE)
b1=(data[,1]-min(data[,1]))/(max(data[,1])-min(data[,1]))
b2=(data[,2]-min(data[,2]))/(max(data[,2])-min(data[,2]))
b3=(data[,3]-min(data[,3]))/(max(data[,3])-min(data[,3]))
b4=(data[,4]-min(data[,4]))/(max(data[,4])-min(data[,4]))
data_scatter=cbind(b1,b2,b3,b4)

data_zscore=scale(data)

i1=ceiling(log(max(abs(data[,1])),10))
c1=data[,1]/10^i1
i2=ceiling(log(max(abs(data[,2])),10))
c2=data[,2]/10^i2
i3=ceiling(log(max(abs(data[,3])),10))
c3=data[,3]/10^i3
i4=ceiling(log(max(abs(data[,4])),10))
c4=data[,4]/10^i4
data_dot=cbind(c1,c2,c3,c4)

options(digits = 4)
data;data_scatter;data_zscore;data_dot

3.连续属性离散化

• 若某些具体数据分析算法要求一些连续的属性需要分类属性，则需做连续属性离散化。
• 常用方法

        等宽法：将属性值分成具有相同宽带的区间。需要人提前分析确定区间数。

        等频法：排序，然后将相同数量的个数放进每个区间。也需要人为划分区间数。

      （一维）聚类法：聚类算法对数据聚类，然后每一簇算一类。

data=read.csv('discretization_data.csv',header = TRUE)

#等高离散化
v1=ceiling(data[,1]*10)

#等频离散化 
names(data)='f'  #变量重命名
attach(data)
seq(0,length(f),length(f)/6) #等频划分为6组
v=sort(f) #按大小排序作为离散化依据
v2=rep(0,930) #定义新变量
for(i in 1:930) v2[i]=ifelse(f[i]<=v[155],1,
                             ifelse(f[i]<=v[310],2,
                                    ifelse(f[i]<=v[465],3,
                                           ifelse(f[i]<=v[620],4,
                                                  ifelse(f[i]<=v[775],5,6)))))
detach(data)

#聚类离散化
result=kmeans(data,6)
v3=result$cluster

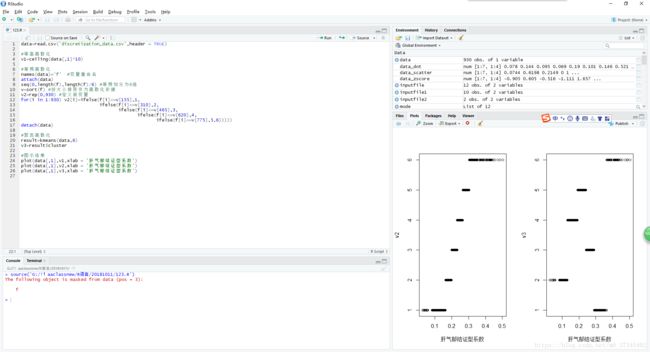
#图示结果
plot(data[,1],v1,xlab = '肝气郁结证型系数')
plot(data[,1],v2,xlab = '肝气郁结证型系数')
plot(data[,1],v3,xlab = '肝气郁结证型系数')

• attach()将对应的数据添加到搜索路径中去，因此其可以直接用分量名来引用。detach()将其从搜索路径中删除。
• kmeans()算法是一种常用的分类算法，具体在下一章介绍，现在只需了解概念，基本做法。
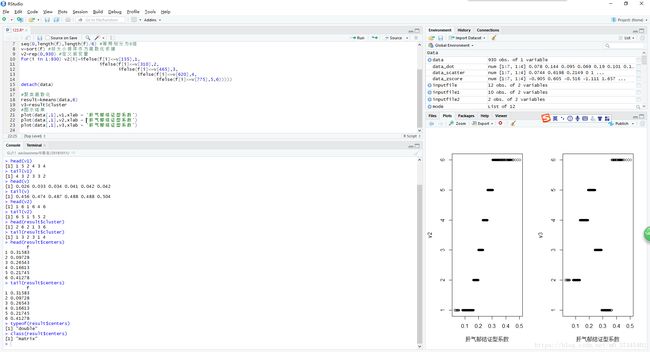
• head(),tail()函数是做什么的？

> head(v1)
[1]1 5 2 4 3 4
> tail(v1)
[1] 4 3 2 3 3 2
> head(v)
[1]0.026 0.033 0.034 0.041 0.042 0.042
> tail(v)
[1] 0.456 0.474 0.487 0.488 0.488 0.504
> head(v2)
[1] 1 6 1 6 4 6
> tail(v2)
[1] 6 5 1 5 5 2
> head(result$cluster)
[1] 2 6 2 1 3 6
> tail(result$cluster)
[1] 1 3 2 3 1 4
> head(result$centers)
        f
1 0.31583
2 0.09728
3 0.26543
4 0.16613
5 0.21745
6 0.41278
> tail(result$centers)
        f
1 0.31583
2 0.09728
3 0.26543
4 0.16613
5 0.21745
6 0.41278
> typeof(result$centers)
[1] "double"
> class(result$centers)
[1] "matrix"

4.属性构造

• 从原始属性中，人为构造出一个新属性，此属性需跟挖掘的目标相关性更大。
• 构造方法根据常识，各种不同挖掘应用有不同的构造方法。

比如进行防窃漏电诊断建模时，已有的属性包括进入线路供入电量、该条线路上各大用户用电量之和，记为供出电量。理论上供入电量和供出电量应该是相等的，但是由于在传输过程中的电能损耗，会使得供入电量略大于供出电量，如果该条线路上的一个或多个大用户存在窃漏电行为，会使供入电量远大于供出电量。反过来，为了判断是否存在有窃漏电行为的大用户，需要构造一个新的关键指标--线损率，该过程就是构造属性，由线户关系图（见图6-1）。新构造的属性线损率计算公式如下：

                      线损率＝（供入电量-供出电量）/供入电量

线损率的范围一般在3%~15%，如果远远超过该范围，就可以认为该条线路的大用户很大可能存在窃漏电等用电异常行为。

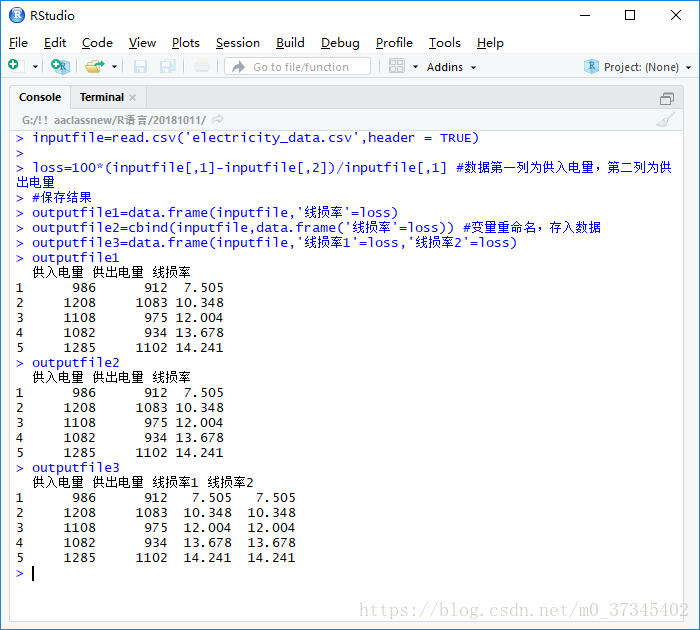
> inputfile=read.csv('electricity_data.csv',header = TRUE)
> 
> loss=100*(inputfile[,1]-inputfile[,2])/inputfile[,1] #数据第一列为供入电量，第二列为供出电量
> #保存结果
> outputfile1=data.frame(inputfile,'线损率'=loss)
> outputfile2=cbind(inputfile,data.frame('线损率'=loss)) #变量重命名，存入数据
> outputfile3=data.frame(inputfile,'线损率1'=loss,'线损率2'=loss)
> outputfile1
  供入电量 供出电量 线损率
1      986      912  7.505
2     1208     1083 10.348
3     1108      975 12.004
4     1082      934 13.678
5     1285     1102 14.241
> outputfile2
  供入电量 供出电量 线损率
1      986      912  7.505
2     1208     1083 10.348
3     1108      975 12.004
4     1082      934 13.678
5     1285     1102 14.241
> outputfile3
  供入电量 供出电量 线损率1 线损率2
1      986      912   7.505   7.505
2     1208     1083  10.348  10.348
3     1108      975  12.004  12.004
4     1082      934  13.678  13.678
5     1285     1102  14.241  14.241

• data.frame()创建数据框的方法复习。
• 当加一列或若干列分量也可以用data.frame()来完成！——新用法
• 当然也可以用cbind函数实现。

4.4数据规约

数据规约的意义

• 降低无效、错误数据对建模的影响，提高建模的准确性。
• 少量且具代表性的数据将大幅缩减数据挖掘所需的时间。

1.属性规约——属性子集选择

• 目标：寻找最小的属性子集，并确保新数据子集的概率分布尽可能接近原数据集的概率分布。
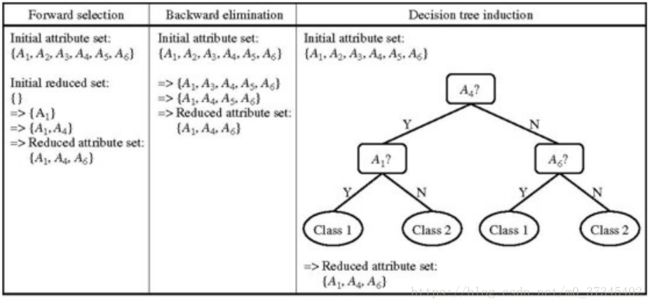
• 属性规约常用方法：合并属性、逐步向前选择、逐步向后删除、决策树归纳、主成分分析。

      合并属性：人为合并（结合属性的实际意义，进行合并）。

      初始属性集：

• 之前的防窃漏电诊断项目时，通过供入电量，供出电量构造出线损率；规约出线损率。

 

• 逐步向前选择：从一个空属性集开始，每次从原来属性集合中选择一个当前最优的属性添加到当前属性子集中。直到无法选择出最优属性或满足一定阈值约束为止。

• 逐步向后删除：该过程由整个属性集开始。在每一步，删除尚在属性集中最差的属性。

      “最好的”（和“最差的”）属性通常使用统计显著性检验来确定。这种检验假定属性是相互独立的。

• 决策树归纳：对初始数据进行分类归纳学习，获得一个初始的决策树。

      不出现在树中的所有属性假定是不相关的。出现在树中的属性形成归约后的属性子集。

      方法的结束标准可以不同。该过程可以使用一个度量阈值来决定何时停止属性选择过程

2.属性规约——维度规约

主成分分析：假定待归约的数据由n个属性或维描述的元组或数据向量组成。主成分分析（principal components analysis）或PCA搜索k个最能代表数据的n维正交向量，其中k≤n。这样，原来的数据投影到一个小得多的空间，导致维度归约。

基本过程：

• 对输入数据规范化，使得每个属性都落入相同的区间。此步有助于确保具有较大定义域的属性不会支配具有较小定义域的属性。
• PCA计算k个标准正交向量，作为规范化输入数据的基。这些是单位向量，每一个方向都垂直于另一个。这些向量称为主成分。输入数据是主成分的线性组合。
• 对主成分按“重要性”或强度降序排列。主成分基本上充当数据的新坐标轴，提供关于方差的重要信息。也就是说，对坐标轴进行排序，使得第一个坐标轴显示数据的最大方差，第二个显示次大方差，如此下去。
• 既然主成分根据“重要性”降序排列，就可以通过去掉较弱的成分（即方差较小）来归约数据的规模。使用最强的主成分，应当能够重构原数据的很好的近似。

• 特征根
• 贡献率
• 特征向量
• 原数据在新坐标系中的坐标值。

> inputfile=read.csv('principal_component.csv',header = FALSE)
> #主成分分析
> PCA=princomp(inputfile,cor = FALSE)
> names(PCA) #查看输出项

> (PCA$sdev)^2  #主成分特征根
 
> summary(PCA)  #主成分贡献率

> PCA$loadings  #主成分载荷

> PCA$scores  #主成分得分

3.数值规约

• 分类：用替代的、较小的数据表示替换或估计数据，如参数模型（只需要存放模型参数，而不是实际数据）或非参数方法，如聚类、抽样和使用直方图
• 直方图：将属性的取值划分为不想交的子集或者桶，用属性值和频数对来替代原来的属性值。
• 聚类：用数据的簇来替换实际数据。
• 抽样：无放回抽样和又放回抽样——从D的N个元组中抽取s个样本（s

      簇抽样：如果D中的元组被分组放入M个互不相交的“簇”，则可以得到簇的s个简单随机抽样（SRS），其中s

      分层抽样：将D划分为不想交的部分，称为“层”，对每一层分别抽样。——人为划分

4.参数回归

线性模型和对数线性模型。