线性回归概率解释(Linear Regression)

模型

监督学习：given a training set, to learn a function h : X → Y so that h(x) is a“good” predictor for the corresponding value of y.

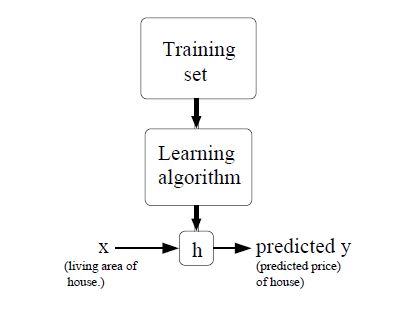
对于线性回归,我们假设可以通过一条直线拟合样本，从而预测y。所以我们假设：

hθ(x)=∑i=0nθixi=θTx

那么 cost function 为：

j(θ)=12∑i=1m(hθ(x(i))−y(i))2

，也就是最小二乘法(LMS)。为了最小化 j(θ) ，我们可以采用批梯度下降法(BGD)、随机梯度下降法(SGD)或者用normal equation直接求 θ 。

接下来从概率的角度来讨论为什么cost function要采用LMS?

Probabilistic interpretation

1. 我们把输入y看成是随机变量。此时，
   y(i)=θTx(i)+ϵ(i).
   
   ϵ 可以代表各种误差，比如测量误差，或者因为其他未知的特征x引起的误差。假设这些误差都是独立同分布的，那么由大数定律可知 ϵ(i)∼N(0,σ2) ，
   
   p(ϵ(i))=12π−−√exp(−(ϵ(i))22σ2).
   
   所以可以得 y(i)|x(i);θ∼N(θTx(i),σ2) ，
   
   p(y(i)|x(i);θ)=12π−−√exp(−(y(i)−θTx(i))22σ2).
   
   注意，这里 p(y(i)|x(i);θ) 不等同于 p(y(i)|x(i),θ) ，前者 θ 默认为是一个固定的值，一个本身就存在的最佳参数矩阵；而后者认为 θ 是一个变量（统计学中frequentist和Bayesian 的差别）。
   此时，我们已知了y的概率分布，因为 ϵ 是独立同分布的，所以每个样本的输出y也是独立同分布的。那么就可以用极大似然估计（MLE）来估计 θ 。似然函数为
   
   L(θ)=∏i=1mp(y(i)|x(i);θ)=∏i=1m12π−−√exp(−(y(i)−θTx(i))22σ2)
   
   ln似然函数得
   ℓ(θ)=logL(θ)=mlog12π−−√σ−1σ2⋅12∑i=1m(y(i)−θTx(i))2.
   
   可以看出，MLE的最终结果就是要最小化
   12∑i=1m(hθ(y(i)−x(i)))2，
   
   这恰好就是我们的cost function。

2.Bayesian线性回归
在一些学习问题中我们经常有上千的feature，如果直接用之前的线性模型，那么我们会发现很容易会导致overfitting。为了防止这个问题我们可以采用贝叶斯方法。
之前我们一直把参数 θ 看成是一个未知的固定值，而贝叶斯学派则把 θ 看成是一个变量。
我们假设 θ 的先验分布是 p(θ)=N(0,τ2I) ,数据集为S.
那么根据贝叶斯公式可知后验分布为

p(θ|S)=p(S|θ)p(θ)p(S)=(∏mi=1p(y(i)|x(i),θ))p(θ)∫θ(∏mi=1p(y(i)|x(i),θ)p(θ))dθ

这里的 p(S|θ) 其实就是在变量 θ 的条件下所以样本数据的似然函数。分母 p(S) 就是不考虑变量 θ 的分布，即对 θ 空间积分。
然后我们可以得到在样本空间条件下的y的分布。

p(y|x,S)=∫θp(y|x,θ)p(θ|S)dθ

最后得到对y的预测期望

E[y|x,S]=∫yyp(y|x,S)dy

由于 θ 的参数空间是高维的，很难积分。所以我们就直接使用了MAP(maximum a posteriori)估计，即最大化 ∏mi=1p(y(i)|x(i),θ)p(θ) ,可以观察到其实Bayesian方法就是在普通线性回归的似然函数中增加了 θ 的前验概率。
和MLE类似我们可以推出最大化 ∏mi=1p(y(i)|x(i),θ)p(θ) 就是要最小化

12∑i=1m(hθ(y(i)−x(i)))2+θ22τ2

也就是在LMS后再加一个regularization项，这就是线性模型的Bayesian linear regression，也可以扩展到polynominal regression个logistic regression。
下面是一张描述Bayesian linear regression的图

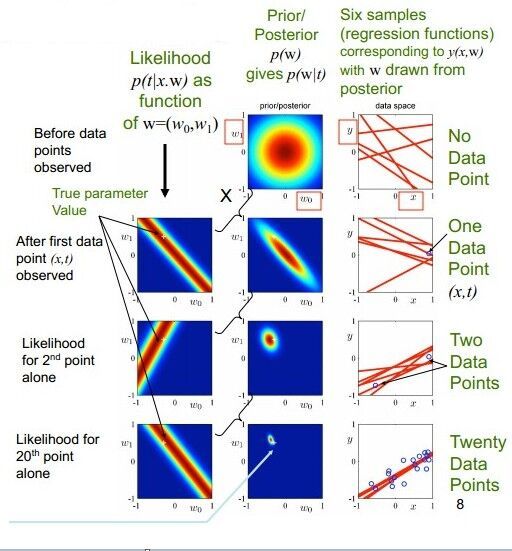
解释： t=y，w=θ ; 当无观察点的时候， θ 的先验分布是圆圈（正态)，然后观察第一个样本点时，得到该样本点可以对应的 θ 空间（第一列第一张图），与开始的先验分布结合就缩小了 θ 空间范围。随观察点增加就进一步确定 θ 。
其实Bayesian Linear regression和ridge regression很相似，其中的概率解释也很复杂，有涉及到无偏估计和检验。但最终目的都是为了防止overfitting和降低模型复杂度。

线性模型的推广-广义线性模型（generalized linear model）

可以知道在普通的线性模型中有如下的假设：
(1).响应变量Y和误差项ϵ正态性：响应变量Y和误差项ϵ服从正态分布，且ϵ是一个具有零均值，同方差的特性。

(2).预测量xi和未知参数βi的非随机性：预测量xi具有非随机性、可测且不存在测量误差；未知参数βi认为是未知但不具随机性的常数。

(3).研究对象：如前所述普通线性模型的输出项是随机变量Y。在随机变量众多的特点或属性里，比如分布、各种矩、分位数等等，普通线性模型主要研究响应变量的均值E[Y]。

E[Y]=E[θTx+ϵ]=θTx

(4).联接方式：所以我们的假设函数 h(x)=θTx 就相当于是预测Y的期望。这里的 h(x) 可以理解为一个响应函数，用来实现从x到y的映射。

此时我们会想到如果Y不是高斯分布会怎么样呢，那响应函数要怎么变化呢？于是可以把线性模型的假设扩展成如下：

(1).响应变量的分布推广至指数分散族(exponential dispersion family)。（正态分布、泊松分布、二项分布、负二项分布、伽玛分布、逆高斯分布都可以转化为指数分布族）

(2).不变

(3).研究对象还是E[Y]。

(4).联接方式：广义线性模型里采用的联连函数(link function)理论上可以是任意的。

既然我们扩展了假设，线性模型就相当于是GLM的一种特例，自然的，我们可以尝试从GLM推出线性模型：
1.首先看指数分布族：

p(y;η)=b(y)exp(ηTT(y)−a(η))

给定T，a，b，我们可以得到一个以 η 为参数的一个分布族。

2.假设（design choice）
对于一个学习问题，我们可以假设:
(1) y|x;θ∼ExponentialFamily(η)
(2)给定 x ，我们要预测的是 E(T(y)|x) ,通常 T(y)=y ,所以有 h(x)=E[y|x]
(3) η=θTx

3.推导
先将高斯分布转化为指数分布，从线性模型可知高斯分布的 σ 对 θ 没有影响，所以为了方便令 σ=1

p(y;μ)=12π−−√exp(−12(y−μ)2)=12π−−√exp(−12y2)⋅exp(μy−12μ2)

即当

ηT(y)a(μ)b(μ)=μ=y=12μ2=12π−−√exp(−12y2)

那高斯分布转化为了指数分布族。
此时的响应函数（response function） h(x) 是

h(x)=E[y|x;θ]（假设2）=μ（因为高斯分布）=η（前面的推导）=θTx（假设3)

推导总结：首先我们假设 y|x∼N(μ,1) ，此时我们是不知道 μ 怎么用x来表示。然后我们把高斯转化为指数分布得出了 μ=θx （其实就是一个响应函数 h(x) ：能最佳匹配y的一个映射函数）。此时 y|x;θ∼N(θTx,1) ，然后通过极大似然估计 L(θ)=∏mi=1p(y(i)|x(i);θ)=∏mi=112π√exp(−(y(i)−θTx(i))22σ2) 就可以估计出 θ 。

对于logistic regression来说也类似：首先我们假设 y|x∼B(ϕ) ，此时我们是不知道 ϕ 怎么用x来表示。然后我们把伯努利转化为指数分布得出了 h(x)=E[y|x]=ϕ=11+e−θTx 此时 y|x∼B(11+e−θTx) ，然后通过极大似然估计就可以估计出 θ 。

参考资料：
【1】cs229 by Andrew Ng from 网易公开课.
【2】PRML.