基于划分的字符串相似性连接
编辑距离是衡量字符串相似度的一种常用方法。编辑距离是指将一个字符串变为另一个字符串所需要的最少的操作次数,其中操作包括插入、删除和替换。字符串相似性连接是指从两个字符串集合中选出所有相似性大于阈值的字符串对。特别的有当两个字符串集合为同一集合时,叫做自连接(self-join)。看过的文章中均以自连接举例子,但无论何种方法都容易扩展到非自连接。
基于编辑距离的连接多数采用q-gram和Trie树两种过滤形式,基于q-gram过滤技术的称为Ed-jion,基于Trie树的称为Trie-join。当字符串集合为人名和位置信息时Ed-join方法低效,这类集合中的字符串长度较短;当字符串集合为文章题目和摘要时Trie-join低效,这类集合中的字符串长度较长。作者针对上述两种缺点,寻找一种与字符串长度无关的有效方法——基于划分的相似性连接。为了描述方便下文中同样以自连接为例进行描述。编辑距离的阈值τ,即两个相似字符串的编辑距离的最大值为τ。
字符串相似性连接常用filter-verification模型,基于划分的字符串连接也不例外的采用了该模型。
1. 划分
1.1 划分的思想
令s为任意一个待划分的字符串,将s划分为τ+ 1部分,最后k = |s|%(τ+ 1)部分中均包括的⌈|s|/(τ+ 1)⌉个字符,前τ+ 1 – k部分中每部分包含⌊s/(τ+ 1)⌋个字符。
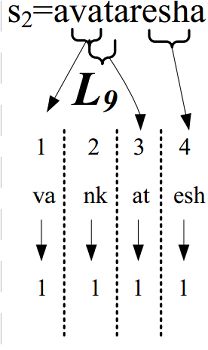
例如s = vankatesh,τ= 3,则k = 1,则 s划分的四部分分别为:va、ak、at、esh。
1.1 划分的用途
若字符串s与字符串r相似,则在r中至少包含一个s的τ+ 1部分划分中的一个,否则字符串s与r的编辑距离大于τ。
易知两个字符串的编辑距离大于等于它们的长度之差,因此只需要比较长度之差小于阈值τ的字符串。具体步骤如下:
(1) 将所有的字符串按长度从小到大排序;
(2) 按从小到大的顺序对字符串建立倒排,长度相同的放到一起;
(3) 对长度为L的字符串建立倒排之前需要检测是否包含长度比其小τ之内的字符串中划分的子字符串;而与当前字符串长度相差大于τ的可从倒排表中删除,减少了存储空间;
(4) 最后一个字符串处理完成后运算结束。
从而可以基于划分达到过滤的效果。
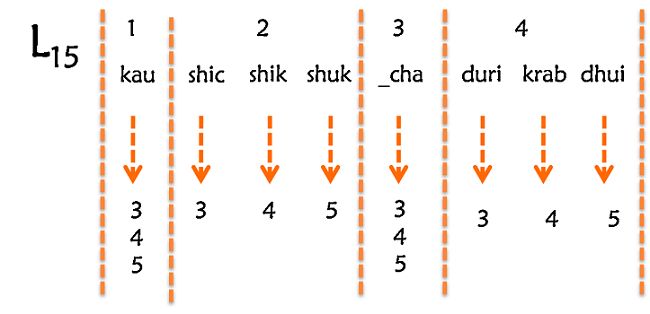
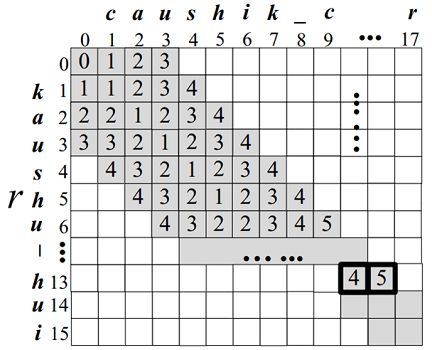
设有三个长度均为15的字符串s1 = “kaushicchaduri”、s2 = “kaushikchakrab”、s3 = “kaushukchadhui”。则长度为15的字符串建立的倒排如图1-1所示。
图1-1 τ = 3时,字符串s1 = “kaushic chaduri”、s2 = “kaushik chakrab”、s3 = “kaushukchadhui”的划分倒排
1.2 需要解决的问题
上述基于划分过滤方法中需要解决如何检测是否包含字符串划分的问题,更深入的在最后验证阶段也有提出了对应的方法。
2. 检测字符串partition
从第1节中可以得出为了过滤需要将每一字符串划分成τ+ 1部分,划分成的每一部分均为一个partition。图2-1为已经按长度排好序的字符串集。
图2-1 字符串集R
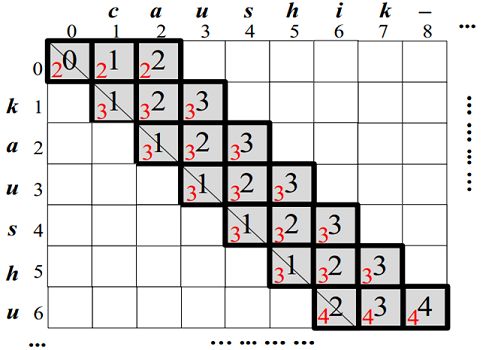
例如:s1的倒排索引如图2-2所示,紧接着我们需要验证字符串s2中是否包含s1倒排中的partition。
方法1:用划分出来的每一个partition去将要建立倒排的字符串s中检测是否包含该partition,若s中包含,则该partition索引的字符串ID均为字符串s的候选字符串相似对。
以图2-2为例说明检测过程,首先取倒排表中的第一个partition(p1 = “va”)去s2中检测是否包含p1。检测到s2包含p1,则p1索引的所有字符串ID均与字符串s2构成候选对。
图2-2 字符串s1的倒排索引和在s2中partition的检测
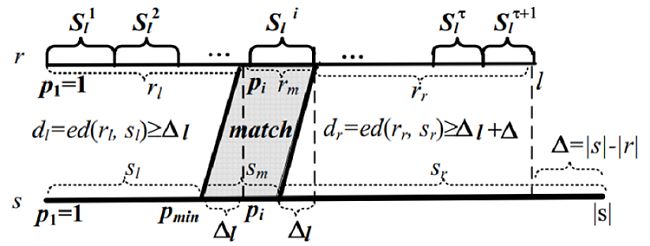
方法2:在方法1中每一个partition都需要跟s2中每个子串的起始位置相比较,根据编辑距离的特征不难发现若字符串r中的每个partition不是在s中的每个起始位置都有效,这里的r只已经建好倒排表的字符串,s是即将建立倒排的字符串,显然有|r| < |s|。即在s中检测pi时只需要检测开始位置为在区间[pi – τ, pi + τ]上的子串是否包含pi。
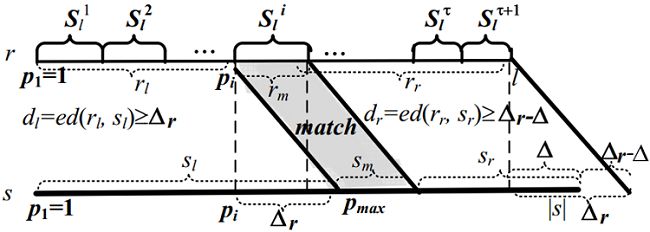
方法3:进一步观察可知,方法2中没有考虑两个字符串之间的长度差,通过计算可以进一步压缩查找范围。如图2-3所示,字符串r和s长度之差为Δ = |s| - |r|,r中pi在s中最小开始位置pmin,则有pmin = max{1, pi - (τ-Δ)/2},公式推导思路为:字符串r与字符串s被pi分成的左右两部分编辑距离只和不能超过τ,具体过程见师兄ppt或论文。同理有图2-4可得pi在s中出现的最优位置pmax= min{|s| - li + 1,pi + (τ+ Δ)/2},其中li指在pi中字符的个数。即在s中检测pi时只需要检测开始位置为在区间[pmin, pmax]上的子串是否包含pi。
图2-3 方法3 pmin求解示意图
图2-4 方法3 pmax求解示意图
方法4:待续……
3. 验证候选对
过滤产生的一系列字符串对成为候选对,在这一部分中将对产生的候选对进行验证,即计算真正的编辑距离。
3.1动态规划法
动态规划为编辑距离的最长用方法。字符串r和s的状态转移方程D [i] [j] = min{ D [i − 1][j]+ 1, D[i][j − 1]+1, D[i − 1][j − 1] + δ )},其中D[i][j]表示字符串r中前i个字符与字符串s中前j个元素的编辑距离,1 ≤ i ≤|r | , 1 ≤ j ≤|s |,若r[i] = s[j]则δ = 0,反之δ = 1。初始值D[i][0] = i,D[0][j] = j。
动态规划求解编辑距离维护的二维表中有D[i-1][j-1] ≤ D[i][j](论文Top-k String Similarity Search with Edit-Distance Constraints中已证明)。因此实际上我们只需要维护宽度为2τ+1带即可,而不需要计算出二位表中的每一个数据,且一旦出现一个编辑距离大于阈值τ该对角线计算终止。如图3-1所示。
优化:同样我们可以结合两个字符串的长度之差进一步减少计算代价。最终可得需要计算的对角线的范围:i - (τ- Δ) / 2 ≤ j ≤ i + (τ+ Δ) / 2。推导过程类似于第二节中方法3的推导过程,详细推导过程见师兄ppt或论文。如图3-2所示。
3.2 扩展法
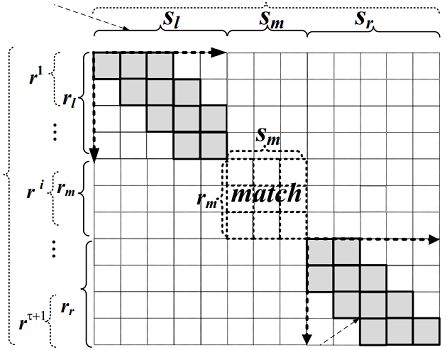
过滤的过程中已经可以判定字符串r与s中已匹配部分,因此可以在具体计算时省略该部分的计算。如图3-3所示。
图3-1 左边为字符串r,上边为字符串s,编辑距离阈值3,编辑距离计算二位表
图3-2左边为字符串r,上边为字符串s,编辑距离阈值3,编辑距离计算二位表
图3-3中sm与rm匹配,则只需要计算rl与sl,rr与sr之间的编辑距离EDl和EDr,则EDl + EDr需小于阈值。若EDl + EDr>τ,则字符串r与s不是最终结果。事实是这样吗?
图3-3 扩展法求解编辑距离
设字符串str1 = “abefcdghij”,str2 = “avecdcdghij”,str1与str2的长度分别为10和11,易得ED(str1, str2) = 3,令编辑阈值τ = 3。若str1中的”cd”与str2中的第一个”cd”相匹配,则str1与str2左边的编辑距离为EDl = 2,右边的编辑距离为EDr = 2,EDl+ EDr > τ,则删除了正确的结果,漏解。若str1中的”cd”与str2中的第二个”cd”相匹配,则str1与str2左边的编辑距离为EDl = 3,右边的编辑距离为EDr = 0,EDl+ EDr < τ。而按照现在的理解应该是记录第一个,但如果是两个都计算还不如动态规划法来得痛快。
3.3 迭代法
……
参考论文:A Partition-Based Method for String Similarity Joins with editdistance constraint