deflate算法总结

一、LZ77算法基本概念

LZ77算法的说明网上很多，本文为个人见解，仅供参考。

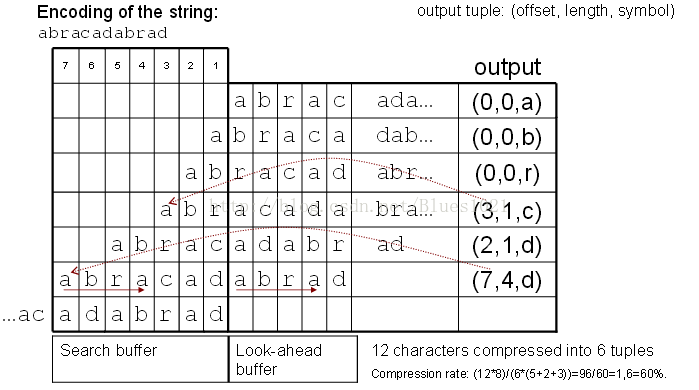
本人认为LZ77算法其实是字典压缩的一个变种，与字典压缩不同的是，它的字典是动态生成的并且只有一个，一般选取一定数量的最近压缩过数据。保存 这些数据的结构叫做滑动窗口，所以LZ77有被常称作滑动窗口算法。至于这么生成字典的原因，其实很简单，因为我们认为一个要压缩的字符串很有可能与上下 文相关，也就是说很有可能在刚压缩的字符串中出现过。要压缩的字符串会与滑动窗口中的字符匹配并用三元组的形式来表示（不懂请看例子），以下的一个 LZ77的压缩例子，能很好的说明此算法的流程，这个例子网上有，本文只是更通俗易懂的展现之。

有一个要压缩的串abcdbbccaaabaeaaabaee

假设前面10个字符已经被压缩，并且设置滑动窗口为10个字符。

窗口	未压缩	相同字符串	相同字符串起始位置	相同字符串长度	相同字符串后一字符	压缩码
abcdbbccaa	abaeaaabaee	ab	0	2	a	(0,2,a)
dbbccaaaba	eaaabaee	null	0	0	e	(0,0,e)
bbccaaabae	aaabaee	aaabae	4	6	e	(4,6,e)

压缩码为(0,2,a)(0,0,e)(4,6,e)

算法其实原理就是这，至于后续工作请查阅其他资料。

加密和解压：

压缩过程：

解压过程：

二、LZ77优化

使用可变偏移和长度域的元组相比固定长度的元组会更好，在小偏移和大小比较小的编码中会比较有优势。

当字符没有找到的时候不要输出(0,0,x)，而是使用0|x或1|0的形式。

使用更加合适的结构体（例如tree,hash set)作为Search buffer或Look ahead buffer,这样可以允许更快的搜索或者更大的缓存。

给元组或者引用加上Huffman 编码，例如LZSS,LZB,LZH,LZR,LZFG,LZMA,Deflate压缩算法等。

改进的LZ77算法+Huffman算法压缩

gzip 对于要压缩的文件，首先使用 lz77 算法进行压缩，对得到的结果再使用 huffman 编码的方法进行压缩。

gzip的LZ77用了哈希容器。

三、Huffman编码

霍夫曼编码模型：思想是压缩数据出现概率高的用短编码，出现概率低的用长编码，且每个字符编码都不一样。

压缩数据单个字符出现的概率抽象为叶子节点的权值，huffman树叶子节点到根节点的编码(是父节点左子节点那么填0，否则填1)

作为字符的唯一编码.

实现时候需要注意的规则：

1）最左的放置在左边，作为父节点的左节点。

2）每次都从没有设置父节点的所用节点中(叶子和分支节点一样对待），从数组小下标到大下标优先顺序遍历。

3）当前搜寻的次数i + n作为新生成的分支节点的数组下标。

实现的过程和具体算法思想：

两个数据结构：

一个是huffman树节点结构体，一个是从霍夫曼树叶子节点编码的结构体。

两个处理过程：

1）建立huffman树：

 基本思想是：对于没有设置父节点的节点集选出最小的两个,最小的放置在左边，次小的放置在右边

 设置好父节点和左右子节点关系，方便获得霍夫曼编码。

2) 从huffman树得到叶子节点的huffman编码：

 基本思想：对于建立好的Huffman树的每个叶子节点，由编码的数组的末端也是从叶子节点最底端，往上遍历

 如果是父节点的左节点那么用编码数组填1，如果是父节点的右节点那么编码数组填0，一直往上追溯到根节点。

 四、deflate无损压缩解压算法（先Lz77压缩，然后huaffman编码)：

 deflate是zip压缩文件的默认算法.   其实deflate现在不光用在zip文件中, 在7z, xz等其他的压缩文件中都用.   实际上deflate只是一种压缩数据流的算法. 任何需要流式压缩的地方都可以用.  

deflate算法下的压缩器有三种压缩模型:
1. 不压缩数据, 对于已经压缩过的数据,这是一个明智的选择. 这样的数据会会稍稍增加, 但是会小于在其上再应用一种压缩算法.
2. 压缩, 先用Lz77, 然后用huffman编码. 在这个模型中压缩的树是Deflate 规范规定定义的, 所以不需要额外的空间来存储这个树.
3. 压缩, 先用LZ77, 然后用huffman编码. 压缩树是由压缩器生成的, 并与数据一起存储.

数据被分割成不同的块, 每个块使用单一的压缩模式. 如过压缩器要在这三种压缩模式中相互切换, 必须先结束当前的块, 重新开始一个新的块.

关于Lz77和huffman如何一起工作的细节需要更进一步的检查. 一旦原始数据被转换成了字符和长度距离对组成的串, 这些数据必须由huffman编码表示.

deflate采用的改进版Lz77算法：

1.三个字节以上的重复串才进行偏码，否则不进行编码：

现在来说明一下，为什么最小匹配为3个字节。这是由于，gzip中，<匹配长度,到匹配串开头的距离>对中，"匹配长度"的范围为3-258，也就是256种可能值，需要8bit来保存。"到匹配串开头的距离"的范围为0-32K，需要15bit来保存。所以一个<匹配长度,到匹配串开头的距离>对需要23位，差一位3个字节。如果匹配串小于3个字节的话，使用<匹配长度,到匹配串开头的距离>对进行替换，不但没有压缩，反而还会增大。所以保存<匹配长度,到匹配串开头的距离>对所需要的位数，决定了最小匹配长度至少要为3个字节。
现在来说明一下，为什么最小匹配为3个字节。这是由于，gzip中，<匹配长度,到匹配串开头的距离>对中，"匹配长度"的范围为3-258，也就是256种可能值，需要8bit来保存。"到匹配串开头的距离"的范围为0-32K，需要15bit来保存。所以一个<匹配长度,到匹配串开头的距离>对需要23位，差一位3个字节。如果匹配串小于3个字节的话，使用<匹配长度,到匹配串开头的距离>对进行替换，不但没有压缩，反而还会增大。所以保存<匹配长度,到匹配串开头的距离>对所需要的位数，决定了最小匹配长度至少要为3个字节。

2.Lz77匹配查找的时候用了哈希表，一个head数组记录最近匹配的位置和prev链表来记录哈希值冲突的之前的匹配位置

如果每次为当前串寻找匹配串时，都要和之前的每个串的至少3个字节进行比较的话，那么比较量将是非常非常大的。为了提高比较速度，gzip使用了哈希表。这是gzip实现LZ77的关键。这个哈希表是一个叫head的数组（后面我们将看到为什么这个缓冲区叫head）。gzip对windows中的每个串，使用串的头三个字节，也就是strstart,strstart 1,strstart 2，用一个设计好的哈希函数来进行计算，得到一个插入位置ins_h。也就是用串的头三个字节来确定一个插入位置。然后把串的位置，也就是 strstart的值，保存在head数组的第ins_h项中。我们马上就可以看到为什么要这样做。head数组在没有插入任何值时，全部为0。
当某处的当前串的三个字节确定了一个ins_h，并把当时当前串的位置也就是当时的strstart保存在了head[ins_h]中。之后另一处，当另一处的当前串的头三个字节，再为那三个字节时，再使用那个哈希函数来计算，由于是同样的三个字节，同样的哈希函数，得到的ins_h必然和前面得到的ins_h是相同的。于是就会发现head[ins_h]不为0。这就说明了，有一个头三个字节和自己相同的串把自己的位置保存在了这里，现在head[ins_h]中保存的值，也就是那个串的开始位置，我们就可以找到那个串，那个串至少前3个字节和当前串的前3个字节相同（稍后我们就可以看到这种说法不准确，这里是为了说明方便），我们可以找到那个串，做进一步比较，看到底能有多长的匹配。

　　我们现在来说明一下，相同的三个字节，通过哈希函数得到的ins_h必然是相同的。而不同的三个字节，通过哈希函数有没有可能得到同一个ins_h，我没有对这个哈希函数做研究，并不清楚，不过一般的哈希函数都是这样的，所以极大可能这里的也会是这种情况，即不同的三个字节，通过哈希函数有可能得到同一个ins_h，不过这并不要紧，我们发现有可能是匹配串之后，还会进行串的比较。

　　一个文件中，可能有很多个串的头三个字节都是相同的，也就是说他们计算得到的ins_h都是相同的，如何能保证找到他们中的每一个串呢？gzip使用一个链把他们链在一起。gzip每次把当前串的位置插入head的当前串头三个字节算出的ins_h处时，都会首先把原来的head[ins_h]的值，保存到一个叫prev的数组中，保存的位置就在现在的strstart处。这样当以后某处的当前串计算出ins_h，发现head[ins_h]不空时，就可以到prev[ head[ins_h] ]中找到更前一个的头三个字节相同的串的位置。对此我们举例说明。

　　例，串
　　 0abcdabceabcfabcg
　　 ^^^^^^^^^^^^^^^^^
　　 01234567890123456

　　整个串被压缩程序处理之后。

　　由abc算出ins_h。
　　这时的head[ins_h]中为 13,即"abcg"的开始位置。
　　这时prev[13]中为 9，即"abcfabcg"的开始位置。
　　这时prev[9]中为 5，即"abceabcfabcg"的开始位置。
　　这时prev[5]中为 1，即"abcdabceabcfabcg"的开始位置。
　　这时prev[1]中为 0。

　　我们看到所有头三个字母为abc的串，被链在了一起，从head可以一直找下去，直到找到0。

　　现在我们也就知道了，三个字节通过哈希函数计算得到同一ins_h的所有的串被链在了一起，head[ins_h]为链头，prev数组中放着的更早的串。这也就是head和prev名称的由
　　来。

　　 gzip寻找匹配串的另外一个值得注意的实现是，延迟匹配。会进行两次尝试。比如当前串为str,那么str发生匹配以后，并不发生压缩，还会对str 1串进行匹配，然后看哪种
　　匹配效果好。

　　例子 ...
从这个例子中我们就看到了做另外一次尝试的原因。如果碰到的一个匹配就使用了的话，可能错过更长匹配的机会。现在做两次会有所改善。

　　 ...

问题讨论

　　我在这里对gzip压缩算法做出了一些说明，是希望可以和对gzip或者压缩解压缩感兴趣的朋友进行交流。
　　我对gzip的了解要比这里说的更多一些，也有更多的例子。如果哪位朋友愿意对下面的问题进行研究，以及其他压缩解压缩的问题进行研究，来这里http://jiurl.cosoft.org.cn/forum/和我交流的话，我也愿意就我知道的内容进行更多的说明。

　　下面是几个问题

　　这种匹配算法，即用3个字节(最小匹配)来计算一个整数，是否比用串比较来得高效，高效到什么程度。

　　哈希函数的讨论。不同的三个字节，是否可能得到同一个ins_h。ins_h和计算它的三个字节的关系。

　　几次延迟尝试比较好？

　　用延迟，两次尝试是否对压缩率的改善是非常有限的？

　　影响lz77压缩率的因素。

　　压缩的极限。

deflate中的huffman编码：

对Lz77得到的压缩后结果，需要统计字符生成编码表huffmantree(指示每个编码代表什么字符）,根据码表对内容进行编码，具体的压缩大小在于精细分配结构体的位域来实现Huffman编码的压缩效果的。

编码表huffmantree和编码后的data都一起放置在文件中。

deflate中的解压：

读取二进制文件，构建huffmantree表，读取数据根据huffmantree生成字符(这些字符是符合LZ77算法的)。

用LZ77解码，这个时候应该需要对窗口生成哈希表（数组+链表)；对解压的数据，进行搜索匹配拷贝替换为相应的串即可。

gzip源码分析

　　 main()中调用函数 treat_file()。
　　 treat_file()中打开文件，调用函数 zip()。注意这里的 work的用法，这是一个函数指针。
　　 zip()中输出gzip文件格式的头，调用 bi_init，ct_init，lm_init，
　　其中在lm_init中将 head初始化清0。初始化strstart为0。从文件中读入64KB的内容到window缓冲区中。
　　由于计算strstart=0时的ins_h，需要0,1,2这三个字节和哈希函数发生关系，所以在lm_init中，预读0,1两个字节，并和哈希函数发生关系。

　　然后lm_init调用 deflate()。
　　 deflate() gzip的LZ77的实现主要deflate()中。

参考总结自下面的文章：

http://blog.csdn.net/brucexu1978/article/details/7469140

http://jens.quicknote.de/comp/LZ77-JensMueller.pdf

http://www.cnblogs.com/shuidao/p/3151067.html