如何通俗地讲解 viterbi 算法？

原文链接

一、通俗地讲解 viterbi 算法

这篇回答你绝对看得懂！如下图，假如你从S和E之间找一条最短的路径，除了遍历完所有路径，还有什么更好的方法？
答案：viterbi (维特比)算法。

过程非常简单：

为了找出S到E之间的最短路径，我们先从S开始从左到右一列一列地来看。

首先起点是S，从S到A列的路径有三种可能：S-A1、S-A2、S-A3，如下图：

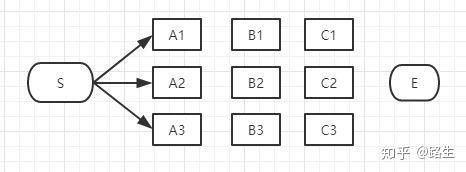
我们不能武断的说S-A1、S-A2、S-A3中的哪一段必定是全局最短路径中的一部分，目前为止任何一段都有可能是全局最短路径的备选项。

我们继续往右看，到了B列。B列的B1、B2、B3逐个分析。

先看B1：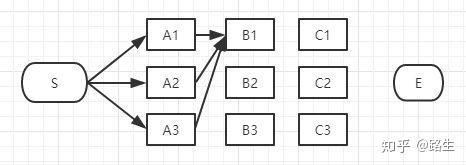
如上图，经过B1的所有路径只有3条：S-A1-B1S-A2-B1S-A3-B1以上这三条路径，我们肯定可以知道其中哪一条是最短的（把各路径每段距离加起来比较一下就知道哪条最短了）。假设S-A3-B1是最短的，那么我们就知道了经过B1的所有路径当中S-A3-B1是最短的，其它两条路径路径S-A1-B1和S-A2-B1都比S-A3-B1长，绝对不是目标答案，可以大胆地删掉了。删掉了不可能是答案的路径，就是viterbi算法（维特比算法）的重点，因为后面我们再也不用考虑这些被删掉的路径了。现在经过B1的所有路径只剩一条路径了，如下图：

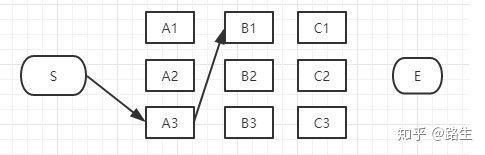
接下来，我们继续看B2：

如上图，经过B2的路径有3条：S-A1-B2S-A2-B2S-A3-B2这三条路径中我们肯定也可以知道其中哪一条是最短的，假设S-A1-B2是最短的，那么我们就知道了经过B2的所有路径当中S-A1-B2是最短的，其它两条路径路径S-A2-B2和S-A3-B1也可以删掉了。经过B2所有路径只剩一条，如下图：

接下来我们继续看B3：

如上图，经过B3的路径也有3条：S-A1-B3S-A2-B3S-A3-B3这三条路径中我们也肯定可以知道其中哪一条是最短的，假设S-A2-B3是最短的，那么我们就知道了经过B3的所有路径当中S-A2-B3是最短的，其它两条路径路径S-A1-B3和S-A3-B3也可以删掉了。经过B3的所有路径只剩一条，如下图：

现在对于B列的所有节点我们都过了一遍，B列的每个节点我们都删除了一些不可能是答案的路径，看看我们剩下哪些备选的最短路径，如下图：
上图是我们我们删掉了其它不可能是最短路径的情况，留下了三个有可能是最短的路径：S-A3-B1、S-A1-B2、S-A2-B3。现在我们将这三条备选的路径汇总到下图：

S-A3-B1、S-A1-B2、S-A2-B3都有可能是全局的最短路径的备选路径，我们还没有足够的信息判断哪一条一定是全局最短路径的子路径。 如果我们你认为没毛病就继续往下看C列，如果不理解，回头再看一遍，前面的步骤决定你是否能看懂viterbi算法（维特比算法）。 接下来讲到C列了，类似上面说的B列，我们从C1、C2、C3一个个节点分析。经过C1节点的路径有：S-A3-B1-C1、S-A1-B2-C1、S-A2-B3-C1
如图：

和B列的做法一样，从这三条路径中找到最短的那条（假定是S-A3-B1-C1），其它两条路径同样道理可以删掉了。那么经过C1的所有路径只剩一条，如下图：

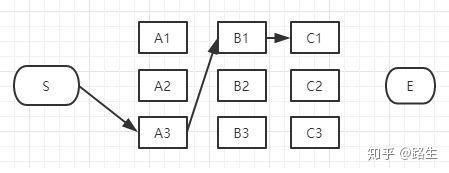
同理，我们可以找到经过C2和C3节点的最短路径，汇总一下：

到达C列时最终也只剩3条备选的最短路径，我们仍然没有足够信息断定哪条才是全局最短。

最后，我们继续看E节点，才能得出最后的结论。
到E的路径也只有3种可能性：

E点已经是终点了，我们稍微对比一下这三条路径的总长度就能知道哪条是最短路径了。

在效率方面相对于粗暴地遍历所有路径，viterbi 维特比算法到达每一列的时候都会删除不符合最短路径要求的路径，大大降低时间复杂度。

viterbi算法果然很简单吧！

python版本实现代码如下：

1.带备忘的自顶向下法

import numpy as np
'''
N为隐藏状态数目
M为观测符号数目
A为状态转移矩阵：N×N
B为观测矩阵：N×M
pi为初始向量：1×N
T为观测序列长度
O为观测序列
'''
def Viterbi(M, N, A, B, pi, T, O):
    delta = np.zeros(shape=(T, N))  # delta为局部概率，即到达某个特殊的中间状态时的概率
    psi = np.zeros(shape=(T, N))  # psi为反向指针，指向最优的引发当前状态的前一时刻的某个状态
    
    # 初始化，计算初始时刻所有状态的局部概率，反向指针均为0
    # delta[0] = pi * B[:, O[1]-1]
    for i in range(N):
        delta[0][i] = pi[i] * B[i][O[0]-1]
        psi[0][i] = 0
    
    # 递推，递归计算除初始时刻外每个时间点的局部概率和反向指针
    for t in range(1, T):
        for i in range(N):
            val = delta[t-1] * A[:, i]  
            # 计算t-1时刻每个状态的局部概率与到t时刻第i个状态的转移概率之积
            maxval = max(val)  
            # 从t-1时刻到t时刻第i个状态的最大概率
            maxvalind = np.argmax(val)  
            # 使从t-1时刻到t时刻第i个状态的概率为最大的t-1时刻的状态序号
            delta[t][i] = maxval * B[i][O[t]-1]  
            # t时刻第j个状态的局部概率
            psi[t][i] = maxvalind  
            # t时刻第i个状态的反向指针
            
    # 终止，观测序列的概率等于T时刻的局部概率
    P = max(delta[T-1])
    I = [0] * T  # q记录找出的隐藏状态路径
    I[T-1] = np.argmax(delta[T-1]) + 1  # T时刻的隐藏状态
    
    # 最优路径回溯
    for t in range(T-2, -1, -1):  # 回溯记录T-1时刻到起始(1)时刻的隐藏状态路径
        I[t] = int(psi[t+1][I[t+1]-1] + 1)  # 由t+1时刻的隐藏状态及其反向指针找到t时刻的隐藏状态，+1是为了输出状态序号1~3，而不是0~2
        
    return I, P, delta

2.自底向上法

这种方法将子问题从小到大进行求解，在T时刻每个状态的最优路径已经全部求解出来，不需要第四步最优路径回溯。

def Viterbi(M, N, A, B, pi, T, O):
    delta = np.zeros(shape=(T, N))  # delta为局部概率，即到达某个特殊的中间状态时的概率
    path = {}  # psi为反向指针，指向最优的引发当前状态的前一时刻的某个状态
 
    # 初始化，计算初始时刻所有状态的局部概率，反向指针均为0
    # delta[0] = pi * B[:, O[1]-1]
    for i in range(N):
        delta[0][i] = pi[i] * B[i][O[0] - 1]
        path[i] = [i]
 
    # 递推，递归计算除初始时刻外每个时间点的局部概率和反向指针
    for t in range(1, T):
        newpath = {}
        for i in range(N):
            maxval, ind = max([(delta[t - 1][j] * A[j][i], j) for j in range(N)])
            # 找到从t-1时刻到t时刻第i个状态的最大概率和使从t-1时刻到t时刻第i个状态的概率为最大的t-1时刻的状态序号
            delta[t][i] = maxval * B[i][O[t] - 1]  # 更新局部概率
            newpath[i] = path[ind] + [i]  # 更新t时刻状态i的最优路径
        path = newpath
 
    # 终止，观测序列的概率等于T时刻的局部概率
    P, last = max([(delta[T - 1][i], i) for i in range(N)])  # 输出最优概率和第T时刻哪个状态(last)达到最优概率
    path[last] = [path[last][i] + 1 for i in range(N)]  # 输出T时刻状态last的最优路径，+1是为了输出状态序号1~3，而不是0~2
 
    return path[last], P, delta

维特比算法的时间复杂度为$$O(T\ast N^2)$$，其中T为观测序列长度，N为隐藏状态数目。(python内置函数max的时间复杂度为$$O(n))$$

通过《统计学习方法》中例10.3来验证算法的正确性：
$$A=\left[\begin{array}{ccc}0.5& 0.2& 0.3\\ 0.3& 0.5& 0.2\\ 0.2& 0.3& 0.5\end{array}\right]，B=\left[\begin{array}{cc}0.5& 0.5\\ 0.4& 0.6\\ 0.7& 0.3\end{array}\right]，\pi =(0.2,0.4,0.4{)}^T$$

观测序列O=(红，白，红)，试求最优状态序列，即最优路径$$I^{\ast }=(i_1^{\ast },i_2^{\ast },...,i_T^{\ast })$$

将模型及序列作为参数传入viterbi函数中：

M = 2
N = 3
A = np.array([[0.5, 0.2, 0.3],
             [0.3, 0.5, 0.2],
             [0.2, 0.3, 0.5]])
B = np.array([[0.5, 0.5],
             [0.4, 0.6],
             [0.7, 0.3]])
pi = np.array([0.2, 0.4, 0.4])
T = 3
O = [1, 2, 1]

计算最优状态序列、最优路径概率、局部概率矩阵：

q, p, delta = Viterbi(M, N, A, B, pi, T, O)
print("最优状态序列：", q)
print("最优路径概率：", p)
print("局部概率矩阵：", delta)

两种方法的结果相同：

最优状态序列： [3, 3, 3]
最优路径概率： 0.014699999999999998
局部概率矩阵： [[0.1     0.16    0.28   ]
 [0.028   0.0504  0.042  ]
 [0.00756 0.01008 0.0147 ]]

与例题中的结果一致。