零知识证明（zero-knowledge proof）

零知识证明（zero-knowledge proof）

在密码学中，零知识证明(zero-knowledge proof)或零知识协议(zero-knowledge protocol)是一种方法，通过该方法，一方（the prover, 证明者）可以向另一方（the verifier, 证明者）证明他们知道值x，而无需传达任何信息，除了他们知道值x。零知识证明的本质是，通过简单地揭示信息来证明某人具有某些信息的知识是微不足道的。面临的挑战是在不透露信息本身或任何其他信息的情况下证明拥有这种财产。[1]

如果证明陈述要求证明者拥有某些秘密信息，那么验证者将无法在不拥有秘密信息的情况下向其他任何人证明该陈述。被证明的陈述必须包括证明者具有此类知识的断言，但不包括知识本身。否则，该语句将不会被证明为零知识，因为它在协议末尾为验证者提供了有关该语句的其他信息。当陈述仅包含证明者拥有秘密信息的事实时，知识的零知识证明就是一个特例。

交互式零知识证明要求证明其知识的个人（或计算机系统）与验证该证明的个人之间进行交互。[1]

实现知识的零知识证明的协议必须必须要求验证者提供交互输入。这种交互式输入通常以一个或多个挑战的形式进行，使得证明者的回答将使验证者确信且仅当陈述为真时，即证明者确实拥有要求保护的知识。如果不是这种情况，验证者可以记录协议的执行并重播以说服其他人他们拥有机密信息。由于重播者确实拥有信息（这意味着协议泄漏了信息，因此不能以零知识证明），因此新的一方的接受是合理的，或者接受是虚假的，即被不接受的人接受实际上拥有信息。

存在一些形式的非交互式零知识证明，[2] [3]，但是证明的有效性取决于计算假设（通常是理想密码哈希函数的假设）。

阿里巴巴洞穴

Jean-Jacques Quisquater等人在他们的论文“如何向孩子解释零知识协议”中首次发表了一个介绍零知识证明的基本思想的著名故事。[4]通常的做法是在零知识证明中将两方标记为Peggy（陈述的证明者）和Victor（陈述的证明者）。

在这个故事中，佩吉（Peggy）发现了用来在山洞中打开魔法门的秘密单词。洞穴的形状像一个环，入口在一侧，魔术门挡住了另一侧。维克多想知道佩吉是否知道这个秘密词。但佩吉（Peggy）是一个非常私密的人，不想向维克多（Victor）透露自己的知识（秘密词）或向整个世界透露自己的知识事实。

他们标记了从入口A和B进入的左右路径。首先，当佩吉（Peggy）进入时，维克多（Victor）在山洞外等着。维克多（Victor）不允许她走哪条路。然后，维克多（Victor）进入山洞，大喊他想让她用来返回的路径名称，随机选择A或B。只要她确实知道魔术字，这很容易：她在必要时打开门，然后沿着所需的路径返回。

但是，假设她不知道这个词。然后，如果维克多（Victor）给出与她输入的路径相同的路径的名称，则她只能按命名路径返回。由于Victor会随机选择A或B，因此她有50％的机会正确猜测。如果他们要重复多次（连续说20次），她成功预期到Victor的所有请求的机会就会越来越小（大约百万分之一）。

因此，如果佩吉（Peggy）反复出现在维克多（Victor）的名字出口处，他可以得出结论，佩吉确实很可能知道这个秘密词。

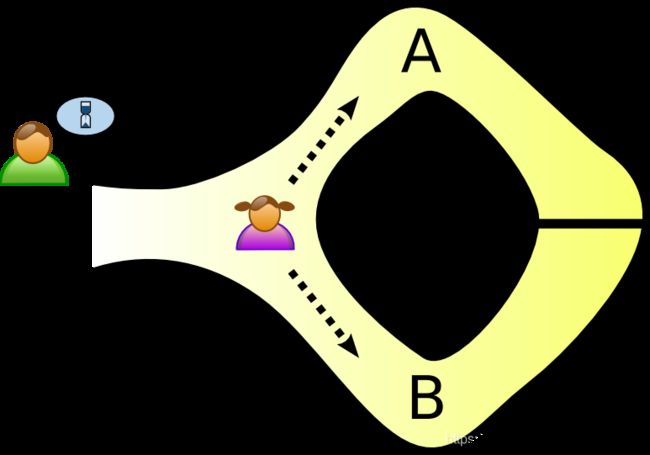
Img 1. Peggy randomly takes either path A or B, while Victor waits outside

Img 2. Victor chooses an exit path

Img 3. Peggy reliably appears at the exit Victor names

关于第三方观察员的一个旁注：即使Victor戴着一个隐藏的摄像机来记录整个交易，但在唯一的情况下，摄像机只能记录Victor大喊“ A！”。和佩吉（Peggy）出现在A处，或者其他情况下，维克多（Victor）喊“ B！这样的录音对于任何两个人来说都是微不足道的（仅要求Peggy和Victor事先同意Victor将大喊A和B的顺序）。这样的录音肯定不会说服原始参加者的。实际上，即使是在原始实验中以观察者身份出现的人也不会令人信服，因为Victor和Peggy可能从头到尾都精心策划了整个“实验”。

进一步注意，如果Victor通过在摄像机上翻转硬币来选择A和B，则该协议将失去其零知识特性；相机上的硬币翻转可能会说服任何以后观看录音的人。因此，尽管这并没有向Victor透露这个秘密词，但它确实使Victor可以说服全世界，佩吉拥有这种知识，这与佩吉的既定愿望背道而驰。但是，数字密码术通常依靠伪随机数生成器来“翻转硬币”，该伪随机数生成器类似于仅具有硬币所有者已知的具有固定的头部和尾部图案的硬币。如果维克多的硬币表现得如此，那么维克多和佩吉又有可能会伪造“实验”，因此使用伪随机数生成器不会像使用翻转硬币那样向世界展示佩吉的知识。将。

请注意，佩吉可以在一次试验中向维克多证明她知道魔语，而没有向他透露。如果Victor和Peggy一起走到洞口，Victor可以看到Peggy穿过A进入并穿过B出来。这可以肯定地证明Peggy知道魔语，而没有向Victor透露魔语。但是，这样的证据可以由第三方观察，也可以由Victor记录，这样的证据对任何人都具有说服力。换句话说，佩吉不能通过声称自己与维克多共谋来反驳这种证据，因此她不再控制谁知道她的知识。

两个球和色盲朋友

想象一下，您的朋友是红绿色盲（当您不在时），您有两个球：一个红色和一个绿色，但在其他方面相同。对您的朋友来说，它们似乎完全相同，他怀疑它们是否真正可区分。您想向他证明它们实际上是不同的颜色，但是没有别的。特别是，您不想透露哪个是红色，哪个是绿色。

这是证明系统。您将两个球交给您的朋友，他把它们放在背后。接下来，他拿起一个球，将球从背后拿出并展示出来。然后，他再次将其放在背后，然后选择只露出两个球之一，以相等的概率随机选择两个球之一。他会问你，“我换球了吗？”然后根据需要重复整个过程。

通过查看它们的颜色，您当然可以确定地说出是否切换颜色。另一方面，如果它们是相同的颜色，因此无法区分，则您不可能以高于50％的概率正确猜测。

由于您将随机成功识别每个开关/非开关的概率为50％，因此在所有开关/非开关上随机成功的概率接近零（“声音”）。如果您和您的朋友多次（例如100次）重复此“验证”，则您的朋友应该确信（“完整性”）这些球的颜色确实不同。

上面的证明是零知识，因为您的朋友永远不会知道哪个球是绿色的，哪个球是红色的；实际上，他对如何区分球一无所知。[5]

扩展

如何通过100行代码实现零知识证明——https://blog.csdn.net/u012386311/article/details/106494902

---

来自维基百科https://en.wikipedia.org/wiki/Zero-knowledge_proof