零知识证明入门理论基础

1 零知识证明概念

零知识证明（Zero-Knowledge Proof，简称ZKP）系统，使得持有相关证据$\omega$的证明者$\mathcal{P}$在不泄露$\omega$的前提下，能够向验证者$\mathcal{V}$证明与$\omega$相关的语句$\iota$是成立的。举例，$\mathcal{P}$知道离散对数难题$(\mathbb{G},g,y)$的解$x$（i.e. $g^x=y$），这里的证据$\omega :=x$，语句$\iota :=“\mathcal{P}知道y的离散对数解”$。

接下来给出ZKP的正式化定义。假设$L\stackrel{\text{def}}{=}\{\iota :\exists \omega \text{s.t.}\mathsf{C}\mathsf{h}\mathsf{e}\mathsf{c}\mathsf{k}(str,\iota ,\omega )=1\}$，$\mathsf{Z}\mathsf{K}\mathsf{P}=(\mathsf{S}\mathsf{e}\mathsf{t}\mathsf{u}\mathsf{p},\mathsf{P}\mathsf{r}\mathsf{o}\mathsf{v}\mathsf{e},\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y},\mathsf{C}\mathsf{h}\mathsf{e}\mathsf{c}\mathsf{k},\mathsf{S}\mathsf{i}\mathsf{m},\mathsf{E}\mathsf{x}\mathsf{t})$是一组六元概率多项式时间算法，

• $\mathsf{S}\mathsf{e}\mathsf{t}\mathsf{u}\mathsf{p}(1^{\lambda })\to str$：初始化算法输入安全参数$\lambda$，输出公共字符串$str$。
• $\mathsf{P}\mathsf{r}\mathsf{o}\mathsf{v}\mathsf{e}(str,\iota ,\omega )\to \pi$：证明算法输入公共字符串$str$，语句$\iota \in L$（其中$L$是NP Language），证据$\omega$，输出证明$\pi$。
• $\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}(str,\iota ,\pi )\to b$：验证算法输入公共字符串$str$，语句$\iota$，证明$\pi$，输出布尔变量$b\in \{0,1\}$，判断$\iota$是否成立。
• $\mathsf{C}\mathsf{h}\mathsf{e}\mathsf{c}\mathsf{k}(str,\iota ,\omega )\to d$：检查算法输入公共字符串$str$，语句$\iota$，证据$\omega$，输出布尔变量$d\in \{0,1\}$，判断$\omega$是否使得$\iota$成立。

ZKP满足如下4个性质：完备性（Completeness）、可靠性（Soundness）、自适应零知识性（Adaptive Zero-Knowledge）和自适应知识论证性（Adaptive Argument of Knowledge）。

• 完备性，若协议双方诚实运行算法，系统出错的概率为可忽略函数，
  $$\begin{gathered} \mathrm{P}\mathrm{r}[str\leftarrow \mathsf{S}\mathsf{e}\mathsf{t}\mathsf{u}\mathsf{p}(1^{\lambda })\wedge \mathsf{C}\mathsf{h}\mathsf{e}\mathsf{c}\mathsf{k}(str,\iota ,\omega )=1 \\ \wedge \pi \leftarrow \mathsf{P}\mathsf{r}\mathsf{o}\mathsf{v}\mathsf{e}(str,\iota ,\omega ):\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}(str,\iota ,\pi )=0]\le \mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(\lambda )。 \end{gathered}$$

• 可靠性，若语句${\iota }^{\ast }\notin L$不成立，那么${\mathcal{P}}^{\ast }$成功忽悠$\mathcal{V}$的概率为可忽略函数，
  $$\begin{gathered} \mathrm{P}\mathrm{r}[str\leftarrow \mathsf{S}\mathsf{e}\mathsf{t}\mathsf{u}\mathsf{p}(1^{\lambda })\wedge {\mathcal{A}}_{{\mathcal{P}}^{\ast }}(str)\to ({\iota }^{\ast },{\pi }^{\ast }) \\ \wedge {\iota }^{\ast }\notin L:\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}(str,{\iota }^{\ast },{\pi }^{\ast })\to 1]\le \mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(\lambda )。 \end{gathered}$$
  （${\mathcal{P}}^{\ast }$右上角带星号代表它是恶意的，$\mathcal{A}$是敌手Adversary或Algorithm的缩写，${\mathcal{A}}_{{\mathcal{P}}^{\ast }}(str)$表示${\mathcal{P}}^{\ast }$将$str$作为输入参数运行算法${\mathcal{A}}_{{\mathcal{P}}^{\ast }}$）

• 自适应零知识性，由于$\iota$本身是NP语句，$\mathcal{V}$难以从$\iota$中学习$\omega$的相关知识，此外，我们期望$\mathcal{P}$与$\mathcal{V}$的交互脚本（transcript）不会进一步泄露$\omega$的相关知识，这里通过模拟器$\mathsf{S}\mathsf{i}\mathsf{m}=({\mathsf{S}\mathsf{i}\mathsf{m}}_1,{\mathsf{S}\mathsf{i}\mathsf{m}}_2)$来刻画该性质（${\mathcal{V}}^{\ast }$即使不与$\mathcal{P}$交互，也可以得到一组“合法”的脚本，“合法”指的是模拟脚本与真实脚本在${\mathcal{V}}^{\ast }$看来不可区分），
  $$\begin{gathered} \mathrm{P}\mathrm{r}[str\leftarrow \mathsf{S}\mathsf{e}\mathsf{t}\mathsf{u}\mathsf{p}(1^{\lambda }):{\mathcal{A}}_{{\mathcal{V}}^{\ast }}^{\mathsf{P}\mathsf{r}\mathsf{o}\mathsf{v}\mathsf{e}(str,\iota ,\omega )}(str)\to 1] \\ -\mathrm{P}\mathrm{r}[(str,td)\leftarrow \mathsf{S}\mathsf{i}{\mathsf{m}}_1(1^{\lambda }):{\mathcal{A}}_{{\mathcal{V}}^{\ast }}^{{\mathsf{S}\mathsf{i}\mathsf{m}}_2(str,td,\iota )}(str)\to 1]\le \mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(\lambda )。 \end{gathered}$$

• 知识论证性质，若${\mathcal{P}}^{\ast }$没有相关证据${\omega }^{\ast }$，那么它针对论断${\iota }^{\ast }$（s.t. $\mathsf{C}\mathsf{h}\mathsf{e}\mathsf{c}\mathsf{k}(str,{\iota }^{\ast },{\omega }^{\ast })=1$）生成一个有效的证明${\pi }^{\ast }$的概率为可忽略函数，这里通过提取器$\mathsf{E}\mathsf{x}\mathsf{t}=({\mathsf{E}\mathsf{x}\mathsf{t}}_1,{\mathsf{E}\mathsf{x}\mathsf{t}}_2)$来刻画该性质（若${\mathcal{P}}^{\ast }$成功伪造一个证明${\pi }^{\ast }$，则$\mathsf{E}\mathsf{x}\mathsf{t}$可以成功从中提取出${\omega }^{\ast }$，这与${\mathcal{P}}^{\ast }$不知道${\omega }^{\ast }$的前提相矛盾），
  $$\begin{gathered} |\mathrm{P}\mathrm{r}[str\leftarrow \mathsf{S}\mathsf{e}\mathsf{t}\mathsf{u}\mathsf{p}(1^{\lambda }):{\mathcal{A}}_{{\mathcal{P}}^{\ast }}(str)\to 1] \\ -\mathrm{P}\mathrm{r}[(str,td)\leftarrow \mathsf{E}\mathsf{x}\mathsf{t}(1^{\lambda }):{\mathcal{A}}_{{\mathcal{P}}^{\ast }}(str)\to 1]|\le \mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(\lambda )， \end{gathered}$$
  且
  $$\begin{gathered} \mathrm{P}\mathrm{r}[(str,td)\leftarrow {\mathsf{E}\mathsf{x}\mathsf{t}}_1(1^{\lambda })\wedge {\mathcal{A}}_{{\mathcal{P}}^{\ast }}(str)\to ({\iota }^{\ast },{\pi }^{\ast })\wedge \mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}(str,{\iota }^{\ast },{\pi }^{\ast })\to 1 \\ \wedge {\mathsf{E}\mathsf{x}\mathsf{t}}_2(str,td,{\iota }^{\ast },{\pi }^{\ast })\to {\omega }^{\ast }:\mathsf{C}\mathsf{h}\mathsf{e}\mathsf{c}\mathsf{k}({\iota }^{\ast },{\omega }^{\ast })=0]\le \mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(\lambda ). \end{gathered}$$

2 零知识证明例子

2.1 Schnorr’s Protocol

这里证明者Alice欲向验证者Bob证明它知道$y$的离散对数解$x$的具体值，双方运行如上$\Sigma$协议。

• 正确性：
  $$g^z=g^{r+cx}={(g^r)(g^x)}^c=a{y}^c。$$

• 零知识性质：模拟器$\mathsf{S}\mathsf{i}\mathsf{m}$构造如下：
  $$\begin{array}{rl}\mathsf{S}\mathsf{i}\mathsf{m}:=& \\ & z\leftarrow {\mathbb{Z}}_q\\ & c\leftarrow {\mathbb{Z}}_q\\ & a=g^z/y^c\end{array}$$
  模拟器输出的脚本$(a,c,z)$与运行协议产生的真实脚本$(a,c,z)$不可区分。

• 知识论证性质：可以这样子想象，${\mathcal{P}}^{\ast }$持有算法${\mathcal{A}}_{{\mathcal{P}}^{\ast }}$却不知道${\omega }^{\ast }$的值，它生成初始参数$a$，然后接收挑战参数$c$，设置程序断点，运行${\mathcal{A}}_{{\mathcal{P}}^{\ast }}$得到对应的$z$，此时${\mathcal{P}}^{\ast }$将程序回滚至断点处，接收新的挑战参数$c^{\prime }$，运行${\mathcal{A}}_{{\mathcal{P}}^{\ast }}$得到对应的$z^{\prime }$，存在
  $$g^z=a{y}^c,g^{z^{\prime }}=a{y}^{c^{\prime }}，$$
  易求
  $$x=(z-z^{\prime })(c-c^{\prime }{)}^{-1}\text{mod}q，$$
  正常$\Sigma$协议运行，一个诚实的证明者$\mathcal{P}$是不允许程序回滚的，否则$\omega$就泄露了，然而上述证明中证明者${\mathcal{P}}^{\ast }$是恶意的，它自己可能也好奇${\omega }^{\ast }$的具体值，因此接受程序回滚（或者说整个协议都是它自己在运行），最后求出${\omega }^{\ast }$的值，这与它不知道${\omega }^{\ast }$的值的前提相矛盾。

扩展阅读：Nils Fleischhacker, Johannes Krupp, Giulio Malavolta, Jonas Schneider, Dominique Schröder, and Mark Simkin. Efficient unlinkable sanitizable signatures from signatures with re-randomizable keys. In Public Key Cryptography, pages 301–330, Taipei, Taiwan, 6-9 March 2016. Springer, Berlin.

2.2 Guillou-Quisquater Protocol

该$\Sigma$协议可用于证明Prover知道某消息$m$的RSA签名。正确性、零知识性质、知识论证性质证明请自行证明。

前驱知识参考资料：
Jonathan Katz and Yehuda Lindell. Introduction to modern cryptography. CRC press, Boca Raton, 2014.
Katz J. Digital signatures[M]. [S.l.]: Springer Science & Business Media, 2010.

2.3 开启石门的神秘咒语

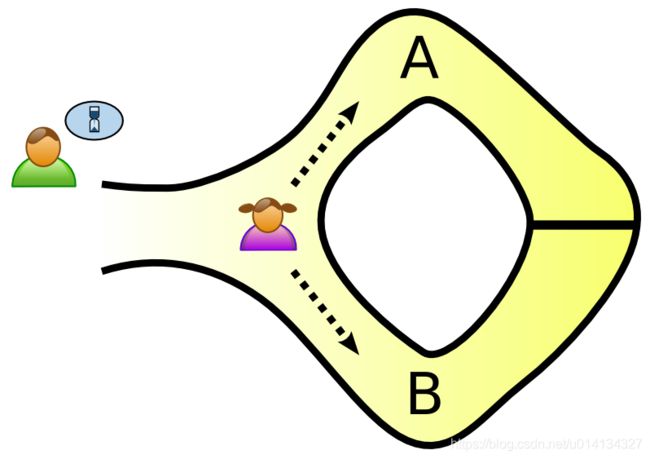
Alice欲向Bob证明她知道打开环形隧道中间石门的神秘咒语，但又不能将咒语泄露给Bob。整个协议运行如下，在Alice进入隧道后，Bob随机喊出一个方向A或B（挑战值），接着Alice从该方向走出来。若Alice一开始从A方向进入，而Bob喊出B方向，除非Alice真的知道神秘咒语$\omega$，否则她不能从B方向出来。若Alice不知道$\omega$，则每次挑战，她成功忽悠Bob的概率为$0.5$，即Alice从A（B）方向进入，而Bob恰巧喊出同方向A（B）。协议运行$\lambda$轮，Alice每次都成功忽悠Bob的概率为$0.5^{\lambda }$，为可忽略函数。

该协议的零知识性质易证明，注意，Bob一开始是不知道Alice进入隧道的方向的，模拟器$\mathsf{S}\mathsf{i}\mathsf{m}$的输出可以是$(A,A,A)$或$(B,B,B)$，这与真实脚本不可区分。若Bob一开始就知道Alice进入隧道的方向，那么模拟器$\mathsf{S}\mathsf{i}\mathsf{m}$则不存在（此时，真实脚本要么是$(A,B,B)$，要么是$(B,A,A)$，与模拟脚本可区分）。

该协议的知识论证性质同样易证明。

3 非交互式零知识证明

在章节2.3“开启石门的神秘咒语”例子中，Bob与Alice之间需要进行$\lambda$轮交互，增加了通信开销和计算开销（注意密码学意义上的随机数生成算法计算开销较大），于是，后来有了非交互式零知识证明（Non-Interactive Zero-Knowledge Proof，简称NIZK）。

这里仅简单介绍随机谕言机模型（Random Oracle，简称RO）下的NIZK怎么设计，以Schnorr’s Protocol为例，验证者Bob先编码出一个性质足够好的哈希函数$\mathsf{H}$，将其发送给证明者Alice，Alice随机挑选$r\leftarrow {\mathbb{Z}}_q$并计算$a:=g^r\text{mod}q$，运行$c:=\mathsf{H}(a\Vert y)$生成挑战$c$，然后计算$z:=r+c\cdot x$，将证明$\pi :=(a,z)$发送给验证者Bob，该过程在生成挑战值$c$阶段就无需与Bob交互。

这里的$\mathsf{H}$被当成随机谕言机使用。注意，当$\mathsf{H}$直接使用$\mathsf{S}\mathsf{H}\mathsf{A}256$等实例化时，NIZK in RO的零知识性质无法证明过去（随机谕言机的重编码性reprogram无法体现），接下来是个人的观点，$\mathsf{H}$应该是具有以下性质的哈希函数：（1）Verifier要保证给定一个输入$a\Vert y$哈希函数$\mathsf{H}$的输出足够随机，使得其分布与$c\leftarrow {\mathbb{Z}}_q$无异，从而使得Prover无法伪造证明；（2）Verifier无法有效说服众人$\mathsf{H}$没有后门，即众人怀疑Verifier在编码$\mathsf{H}$时有可能故意先计算$z\leftarrow {\mathbb{Z}}_q$、$c\leftarrow {\mathbb{Z}}_q$和$a:=g^z/y^c$，并故意令$\mathsf{H}(a\Vert y)=c$，但Verifier无法有效反驳该观点（当Prover意识到Verifier能够有效反驳该观点时，Prover应该立即拒绝给出证明$\pi$）。

想象一个极端例子，$y$的离散对数答案$x$超级值钱，Alice拟向Bob炫耀她知道$x$的值，运行NIZK in RO，若$\mathsf{H}$的输出不够随机，那么Alice有可能找到一组特别的模拟脚本$(a,c,z)$恰巧对应$\mathsf{H}$的输入和输出，以此来欺骗Bob；若$\mathsf{H}$完全没有后门，Bob有可能起嫉妒心，向强盗透露Alice知道$x$的值，从而使得Alice遭到追杀。

如何构造这样一个$\mathsf{H}$函数，接下来纯粹是个人想法：将$a\Vert y$输入到$\mathsf{S}\mathsf{H}\mathsf{A}256$中得到哈希值$h$，将该哈希值$h$映射到${\mathbb{Z}}_q$的元素$c$上，这张映射表由Verifier编码，从而实现重编码性。由于$\mathsf{S}\mathsf{H}\mathsf{A}256$被当成RO来用，即使映射表固定，$\mathsf{H}$的输出对于Prover来说是随机的。

例如，在章节2.3“开启石门的神秘咒语”例子中，假设原先交互$k$轮，现Verifier对$\mathsf{H}$的编码为$\mathsf{H}:=(\mathsf{S}\mathsf{H}\mathsf{A}256,映射表1,映射表2,\dots ,映射表k)$；在章节2.1“Schnorr’s Protocol”例子中，若${\mathbb{Z}}_q$有1024bit，而SHA256有256bit，则使用4个带秘钥的SHA256来实现1024bit。映射表可以编码成1、2、3等形式，表示向下循环移位1个元素、2个元素、3个元素等。