(开源)粒子群算法求解优化问题,参数分析(以求二维sphere最小值为例)
粒子群算法求解优化问题
目录
1.粒子群算法的解读
1.1预准备
1.1.1 十进制编码
1.1.2 初始化群体的设定
1.1.3 适应度函数的设定
1.2基本思想
1.3基本原理
1.4算法定义
1.5基本的PSO算法
1.6 算法流程图
1.7 优缺点
2.粒子群算法的验证
2.1编码
2.2初始化群体的设定
2.3适应度函数的设定
2.4控制参数设定
3.粒子群算法的参数解读
3.1初始参数运行结果:
3.2 惯性权重因子(w)对结果的影响
3.2.1 w = 0.3
3.2.2 w = 0.7
3.2.3 w = 1.5
3.2.4 w = 2.5
3.2.5总结
3.3认知权重因子(c1)对结果的影响
3.3.1 c1 = 0.5
3.3.2 c1 = 1
3.3.3 c1 = 2
3.3.4 c1 = 2.5
3.3.5总结
3.4社会权重因子(c2) 对结果的影响
3.4.1 c2 = 0.5
3.4.2 c2 = 1
3.4.3 c2 = 2
3.4.4 c2 = 2.5
3.4.5总结
3.5迭代次数(maxgen) 对结果的影响
3.5.1 maxgen = 20
3.5.2 maxgen = 40
3.5.3 maxgen = 100
3.5.4 maxgen = 1000
3.5.5总结
3.6最大、最小速度(Vmax,Vmin) 对结果的影响
3.6.1 Vmax=0.5,Vmin= - 0.5
3.6.2 Vmax=1,Vmin= - 1
3.6.3 Vmax=3,Vmin= - 3
3.6.4 Vmax=4,Vmin= - 4
3.6.5总结
3.7优参数带入的的结果
4粒子群算法的程序源码
4.1 主函数
4.2 fun函数
1.粒子群算法的解读
粒子群算法可包含以下基本要素
1.1预准备
1.1.1 十进制编码
染色体上的基因是以0,1,2,3,4,5,6,7,8,9的形式保存的。
优点:
采用实数表达法不必进行数制转换,可直接在解的表现型上进行粒子群操作;用于求解高维或者复杂的优化问题。
1.1.2 初始化群体的设定
随机产生一些个体
1.1.3 适应度函数的设定
若目标函数f(x)为最大化(求最大值)问题,那么适应度函数取为
F(f(x))= f(x)
若目标函数f(x)为最小化(求最小值)问题,那么适应度函数取为
F(f(x))= 1/f(x)
1.2基本思想
将群体中的每个个体看作n维搜索空间中一个没有体积、没 有质量的粒子,在搜索空间中以一定的速度飞行,通过群体 粒子间的合作与竞争产生的群体智能指导优化搜索。
每个粒子有一个由适应度函数决定的适应值。
1.3基本原理
PSO初始化为一群随机粒子,然后通过迭代找到最优解。在 每一次迭代中,粒子通过跟踪两个“极值”来更新自己。第 一个就是粒子本身所找到的最优解,这个解称为个体极值。 另个一是整个种群目前找到的最优解,这个解称为全局极值。
1.4算法定义

1.5基本的PSO算法


1.6 算法流程图
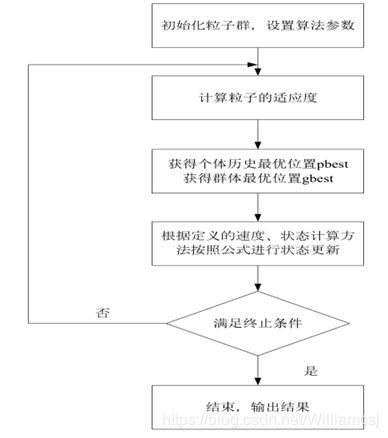
1.7 优缺点
优点:
- 易于描述,易于理解。
- 对优化问题定义的连续性无特殊要求。
- 只有非常少的参数需要调整。
- 算法实现简单,速度快。
- 相对其它演化算法而言,只需要较小的演化群体。
- 算法易于收敛,相比其它演化算法,只需要较少的评价函数计算次数就可达到收敛。
- 无集中控制约束,不会因个体的故障影响整个问题的求解,确保了系统具备很强的鲁棒性。
缺点:
- 对于有多个局部极值点的函数,容易陷入到局部极值点中,得不到正确的结果。
- 由于缺乏精密搜索方法的配合,PSO方法往往不能得到精确的结果。
- PSO方法提供了全局搜索的可能,但并不能严格证明它在全局最优点上的收敛性。因此,PSO一般适用于一类高维的、存在多个局部极值点而并不需要得到很高精度的优化问题。
2.粒子群算法的验证
我将我对掌握程度,并用求测试函数二维Sphere函数(f(x1,x2) = x1x1 +x2x2[-100,100])的最小值来验证。
2.1编码
我们将自变量x1,x2采用十进制编码。
2.2初始化群体的设定
为了更好的找到测试函数Sphere的最小值,我们初始选取了100当成种群规模。
2.3适应度函数的设定
由于我们是找Sphere函数的最小值,那么适应度函数取为
F(f(x1,x2))= 1/f(x1,x2)
2.4控制参数设定
- 惯性权重因子w = 1
- 认知权重因子c1 = 1.5
- 社会权重因子c2 = 1.5
- 迭代次数maxgen = 50
- 粒子移动的最大最小速度Vmax = 2;Vmin = -2
3.粒子群算法的参数解读
3.1初始参数运行结果:
- 惯性权重因子w = 1
- 认知权重因子c1 = 1.5
- 社会权重因子c2 = 1.5
- 迭代次数maxgen = 50
- 粒子移动的最大最小速度Vmax = 2;Vmin = -2
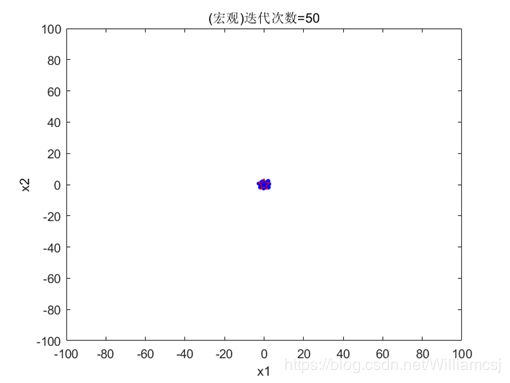
图3.1.1粒子分布(宏观)
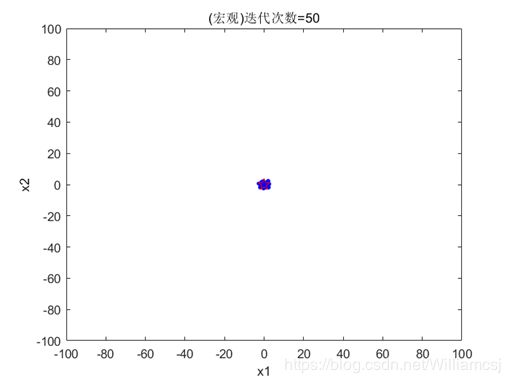
图3.1.2粒子分布(微观)
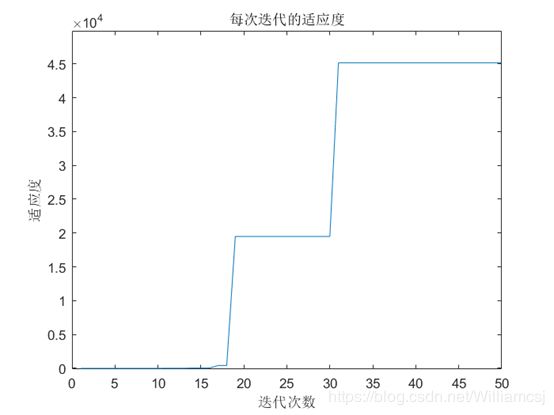
图3.1.3 每次迭代的适应度

3.2 惯性权重因子(w)对结果的影响
由于我们之前设定的是惯性权重因子w=1。为了更好的观察出惯性权重因子(w)对结果的影响,且要避免偶然性。则我们以w=1为分界,分别在此左右各取两个不同的值,其它参数不变。
3.2.1 w = 0.3
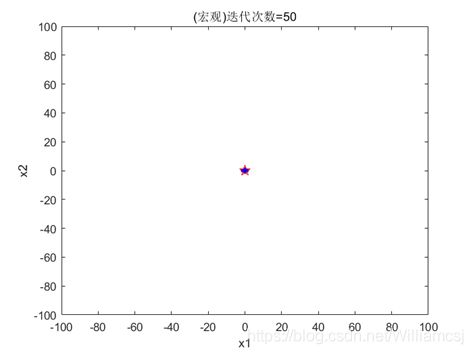
图3.2.1.1粒子分布(宏观)
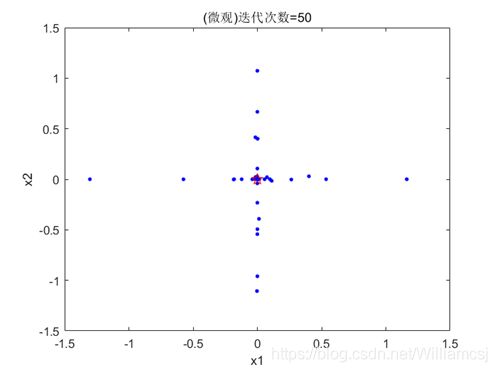
图3.2.1.2粒子分布(微观)
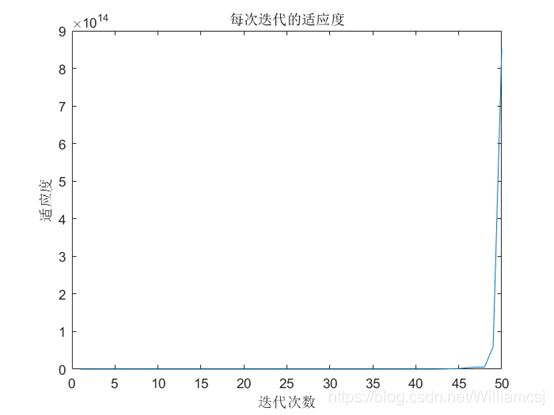
图3.2.1.3 每次迭代的适应度

3.2.2 w = 0.7
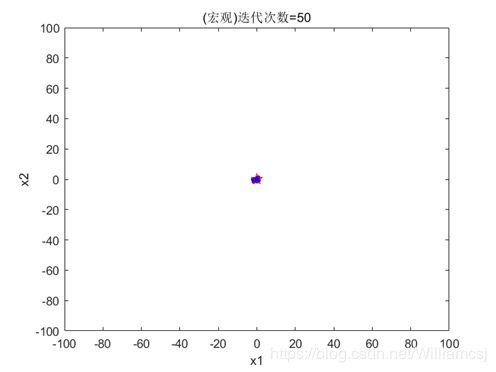
图3.2.2.1粒子分布(宏观)
![]()
图3.2.2.2粒子分布(微观)
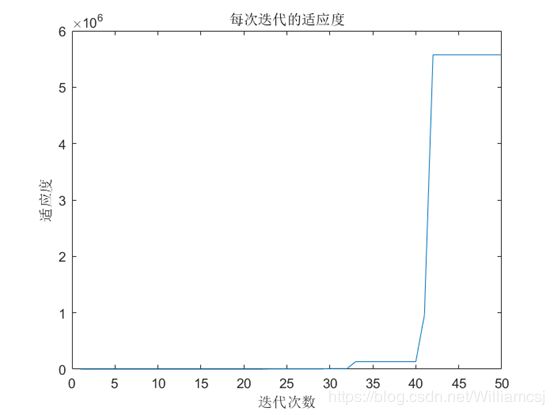
图3.2.2.3 每次迭代的适应度

3.2.3 w = 1.5
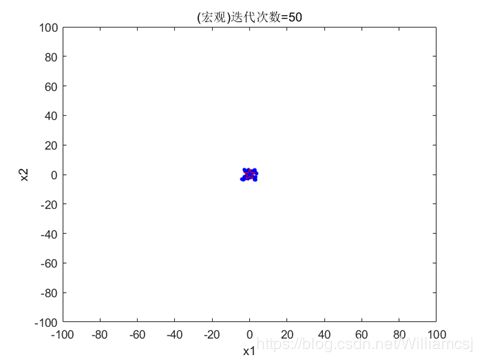
图3.2.3.1 粒子分布(宏观)
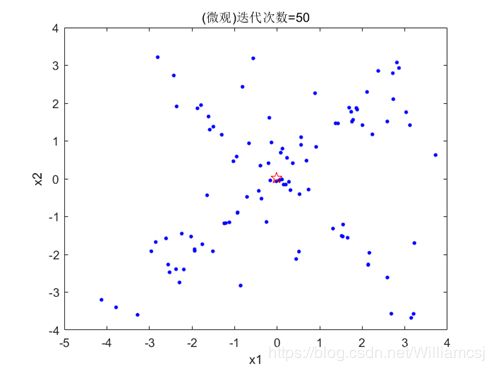
图3.2.3.2粒子分布(微观)
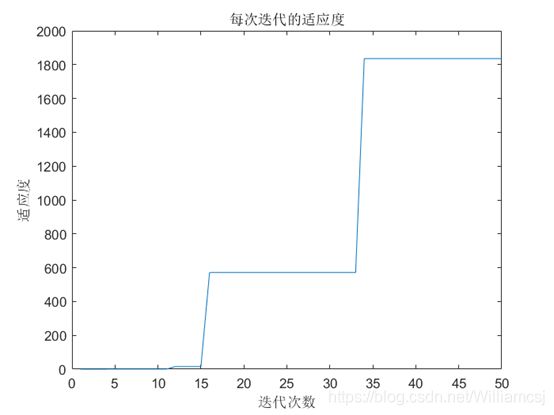
图3.2.3.3 每次迭代的适应度

3.2.4 w = 2.5
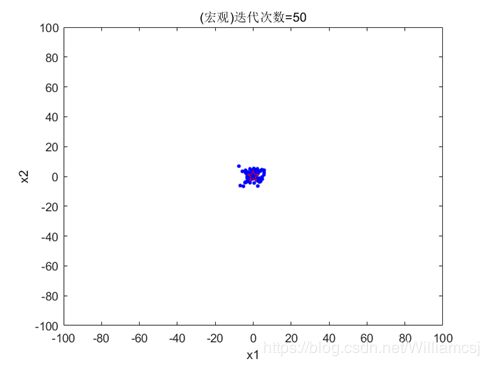
图3.2.4.1 粒子分布(宏观)

图3.2.4.2 粒子分布(微观)
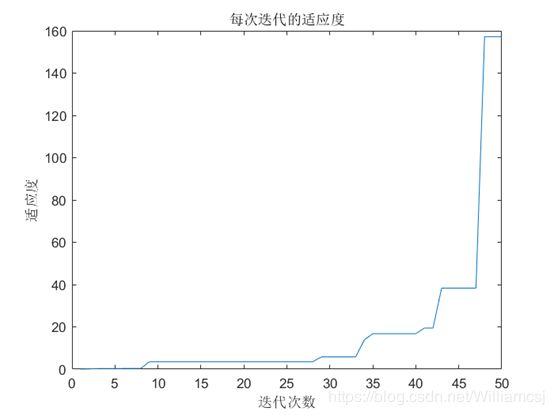
图3.2.4.3 每次迭代的适应度

3.2.5总结
通过以上的实验,我们可以发现,当在这种初始条件下且只改变了惯性权重,当惯性权重w的增大,最优适应度越小,算出来的结果也越远离已知的最优解。
3.3认知权重因子(c1)对结果的影响
由于我们之前设定的是权重因子c1= 1.5。为了更好的观察出权重因子(c1)对结果的影响,且要避免偶然性。则我们以c1 = 1.5为分界,分别在此左右各取两个不同的值,其它参数不变。
3.3.1 c1 = 0.5
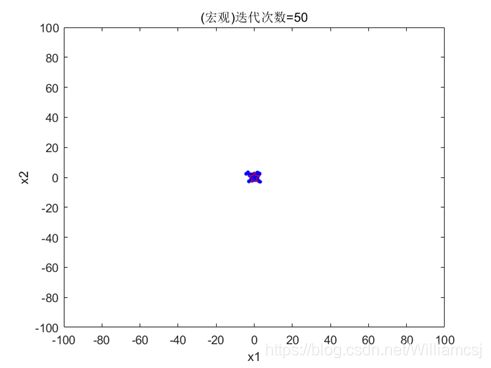
图3.3.1.1 粒子分布(宏观)
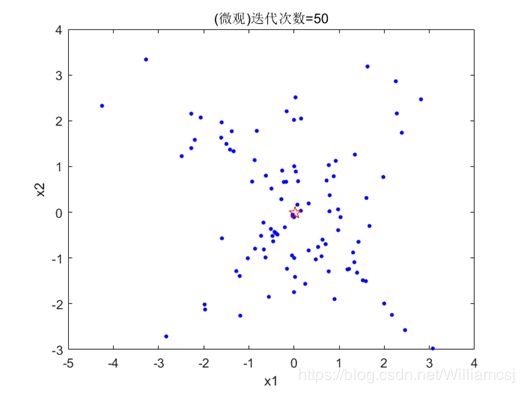
图3.3.1.2 最优点坐标
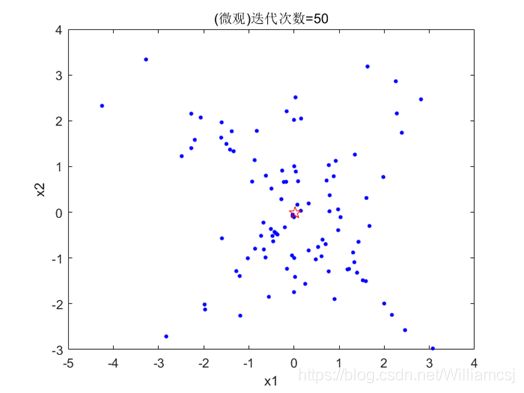
图3.3.1.3 每次迭代的适应度

3.3.2 c1 = 1
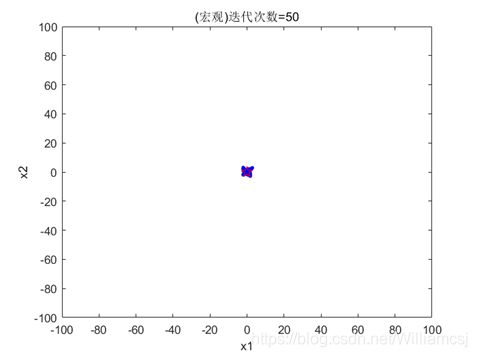
图3.3.2.1 粒子分布(宏观)
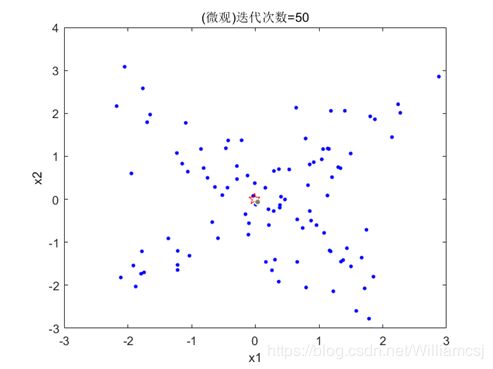
图3.3.2.2 粒子分布(微观)
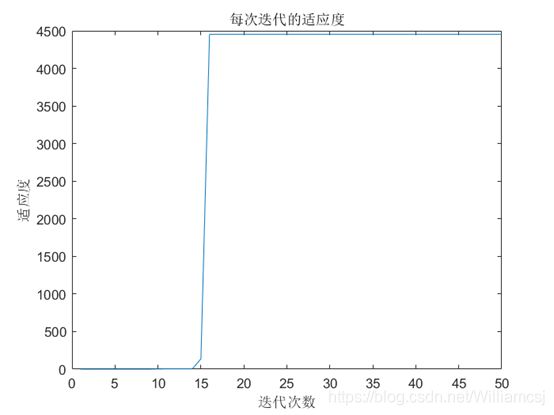
图3.3.2.3 每次迭代的适应度

3.3.3 c1 = 2
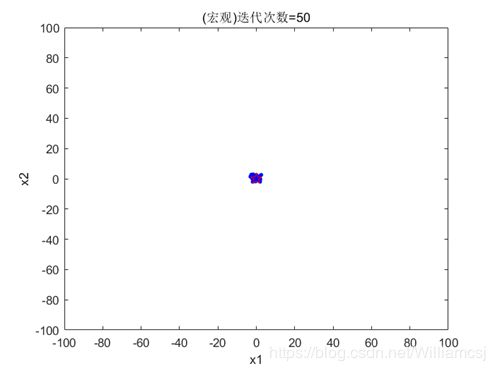
图3.3.3.1 粒子分布(宏观)
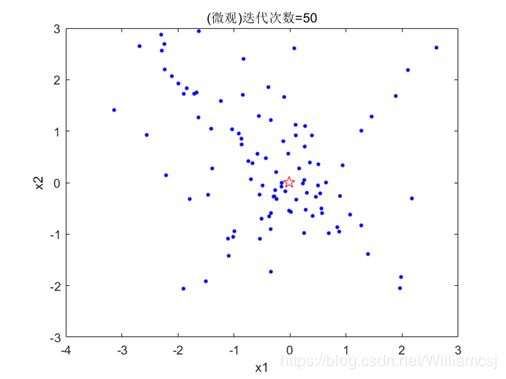
图3.3.3.2 粒子分布(微观)
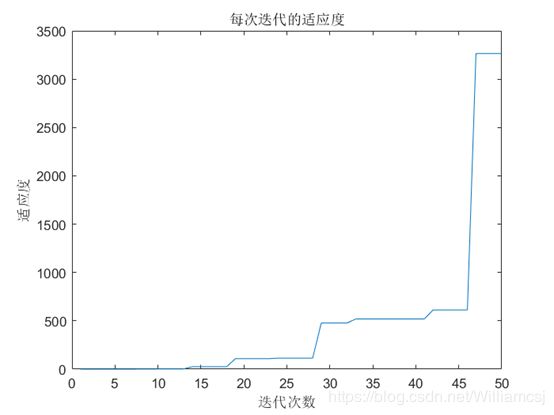
图3.3.3.3 每次迭代的适应度

3.3.4 c1 = 2.5
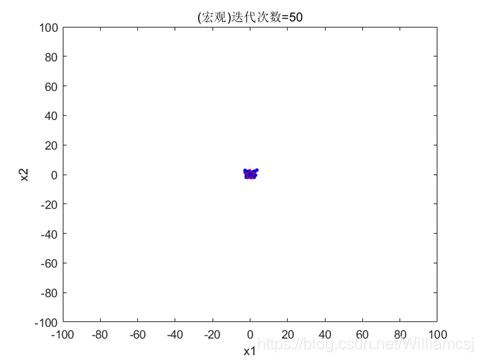
图3.3.4.1 粒子分布(宏观)
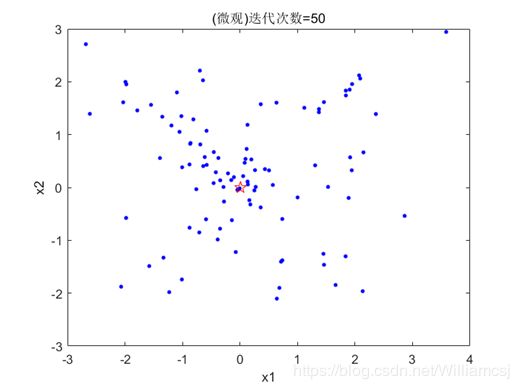
图3.3.4.2 粒子分布(微观)
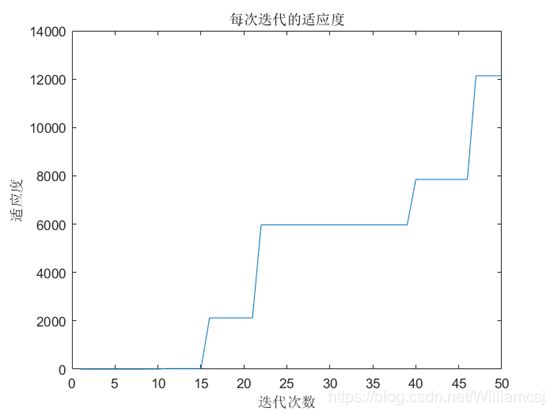
图3.3.4.3 每次迭代的适应度

3.3.5总结
通过以上的实验,我们可以发现,当在这种初始条件下且只改变了认知权重c1时,当认知权重c1的增大,最优适应度先增大后减小,且c1=1.5左右时,效果最好,最优适应度最大。
3.4社会权重因子(c2) 对结果的影响
由于我们之前设定的是社会权重因子c2=1.5。为了更好的观察出社会权重因子(c2)对结果的影响,且要避免偶然性。则我们以为c2=1.5分界,分别在此左右各取两个不同的值,其它参数不变。
3.4.1 c2 = 0.5
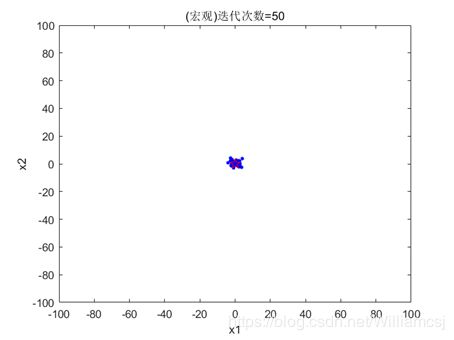
图3.4.1.1 粒子分布(宏观)
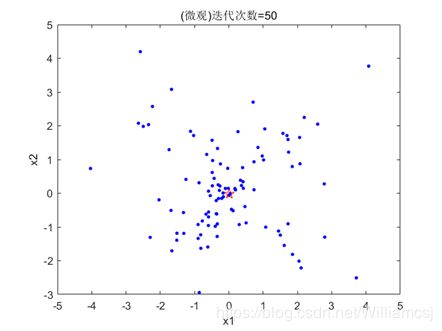
图3.4.1.2 粒子分布(微观)
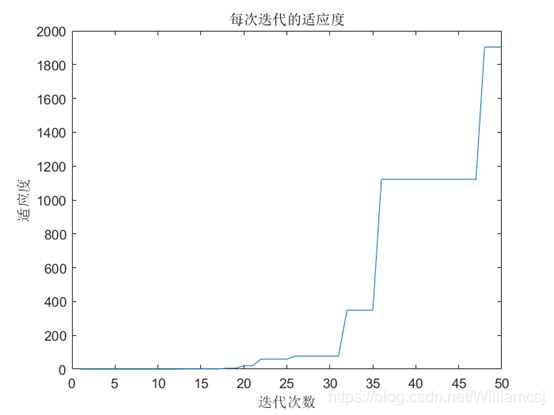
图3.4.1.3 每次迭代的适应度

3.4.2 c2 = 1
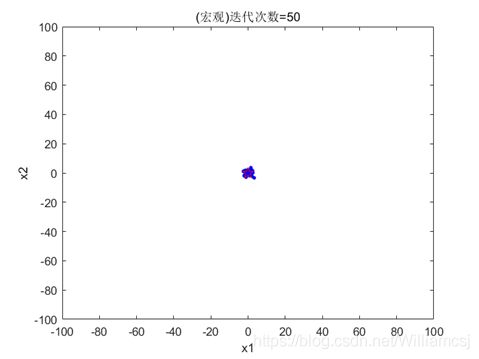
图3.4.2.1 粒子分布(宏观)
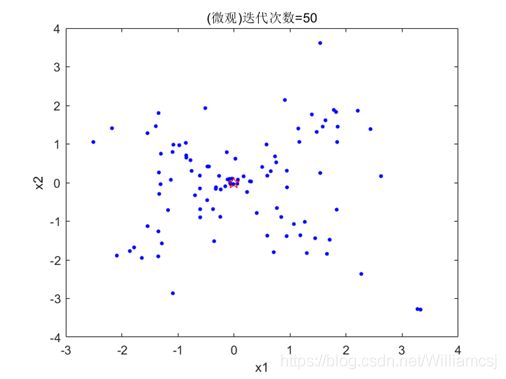
图3.4.2.2 粒子分布(微观)
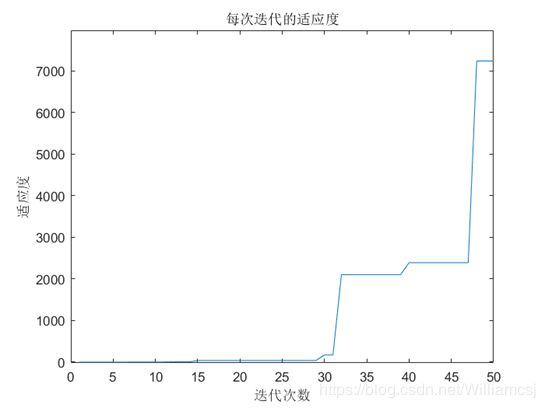
图3.4.2.3 每次迭代的适应度

3.4.3 c2 = 2
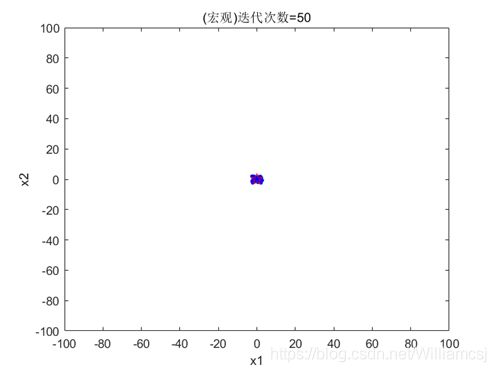
图3.4.3.1 粒子分布(宏观)
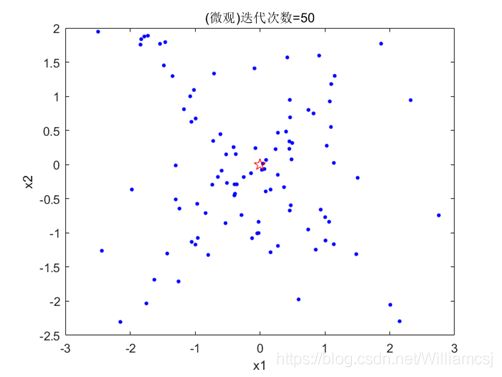
图3.4.3.2 粒子分布(微观)
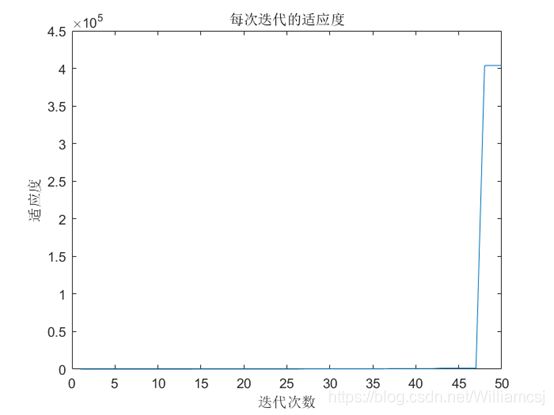
图3.4.3.3 每次迭代的适应度

3.4.4 c2 = 2.5
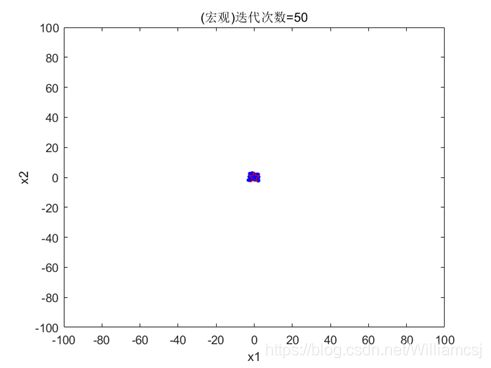
图3.4.4.1 粒子分布(宏观)
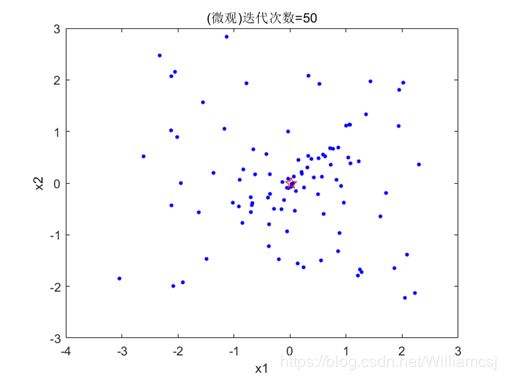
图3.4.4.2 粒子分布(微观)
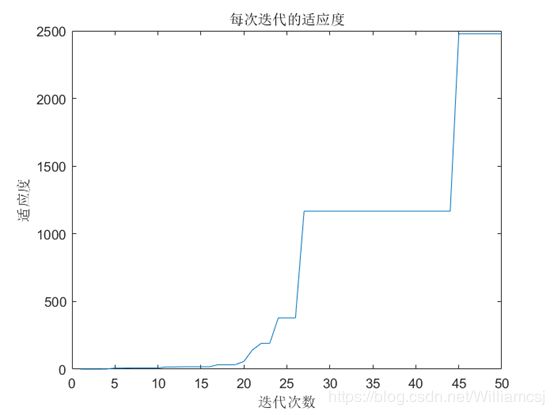
图3.4.4.3 每次迭代的适应度

3.4.5总结
通过以上的实验,我们可以发现,当在这种初始条件下且只改变了社会权重c2时,当社会权重c2的增大,最优适应度先增大后减小,且c2=2.0左右时,效果最好,最优适应度最大。
3.5迭代次数(maxgen) 对结果的影响
由于我们之前设定的是迭代次数maxgen = 50。为了更好的观察出迭代次数(maxgen)对结果的影响,且要避免偶然性。则我们以maxgen = 50为分界,分别在此左右各取两个不同的值,其它参数不变。
3.5.1 maxgen = 20
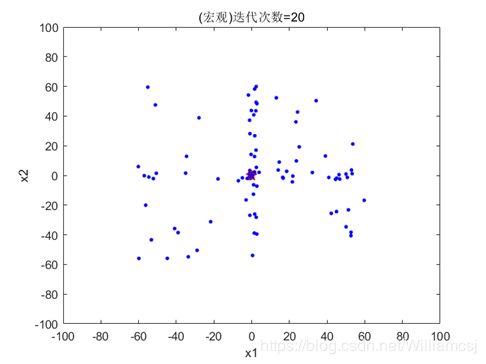
图3.5.1.1 粒子分布(宏观)
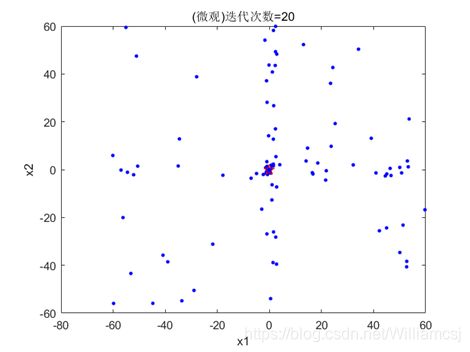
图3.5.1.2 粒子分布(微观)
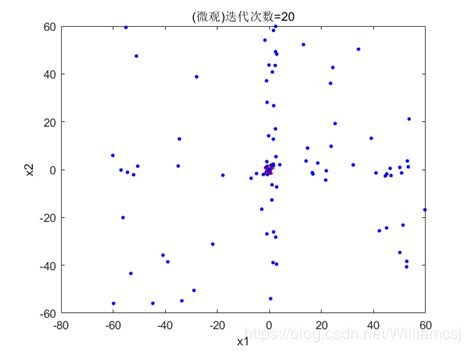
图3.5.1.3 每次迭代的适应度

3.5.2 maxgen = 40
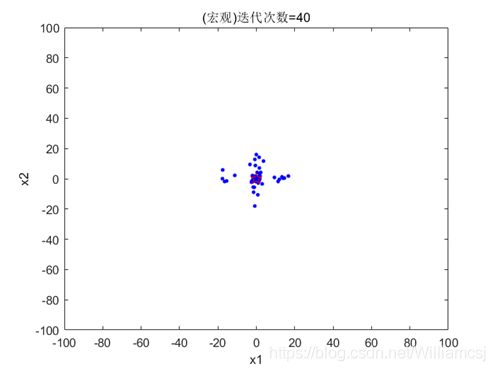
图3.5.2.1 粒子分布(宏观)
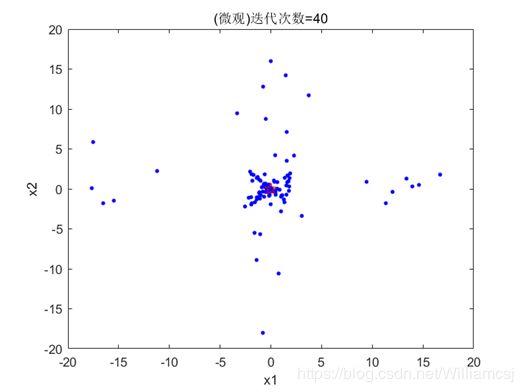
图3.5.2.2 粒子分布(微观)
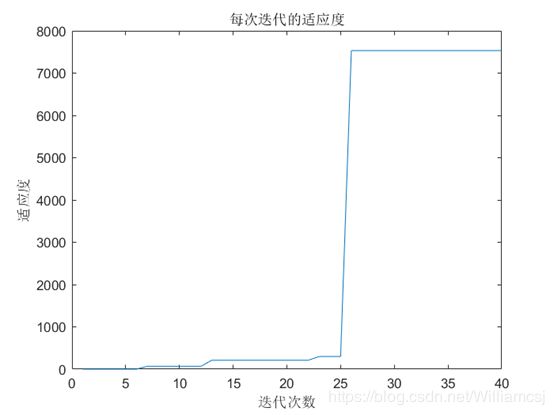
图3.5.2.3 每次迭代的适应度

3.5.3 maxgen = 100
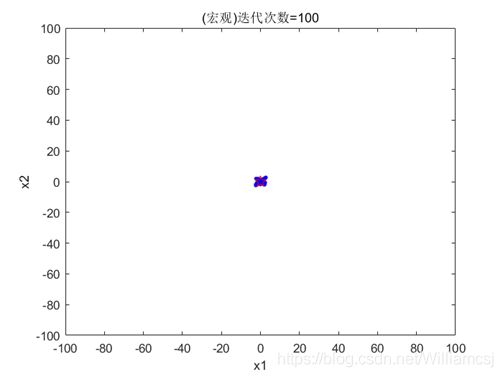
图3.5.3.1 粒子分布(宏观)
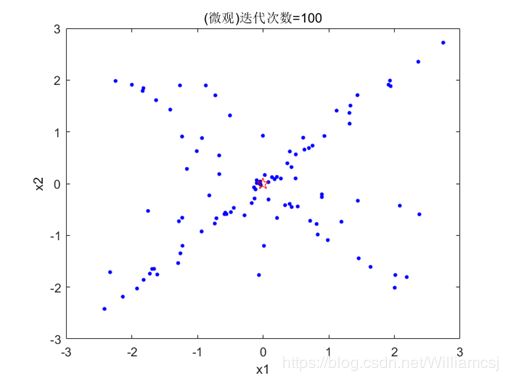
图3.5.3.2 粒子分布(微观)
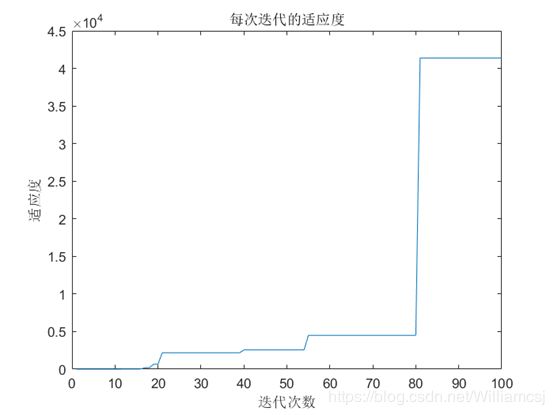
图3.5.3.3 每次迭代的适应度

3.5.4 maxgen = 1000
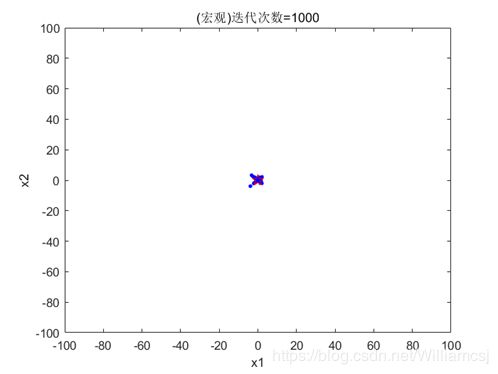
图3.5.4.1 粒子分布(宏观)
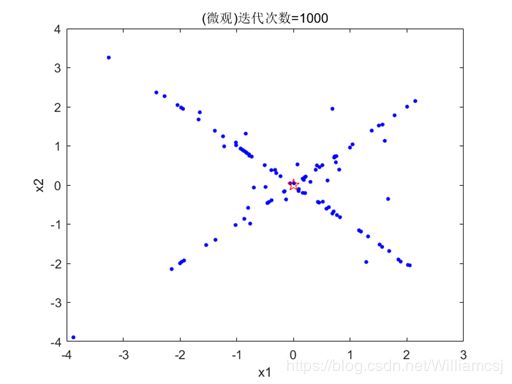
图3.5.4.2 粒子分布(微观)
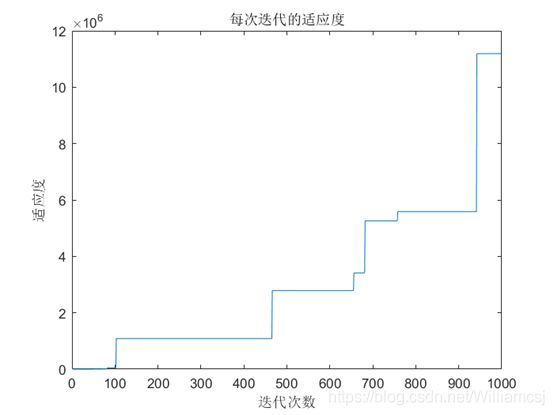
图3.5.4.3 每次迭代的适应度

3.5.5总结
通过以上的实验,我们可以发现,当在这种初始条件下且只改变了迭代次数maxgen时,当迭代次数maxgen的增大,最优适应度也随之增大,最优适应度也随之增大。
3.6最大、最小速度(Vmax,Vmin) 对结果的影响
由于我们之前设定的是最大速度Vmax=2,最小速度Vmin= - 2。为了更好的观察出最大速度Vmax,最小速度Vmin对结果的影响,且要避免偶然性。则我们以最大速度Vmax=2,最小速度Vmin= - 2为分界,分别在此左右各取两个不同的值,其它参数不变。
3.6.1 Vmax=0.5,Vmin= - 0.5

图3.6.1.1 粒子分布(宏观)
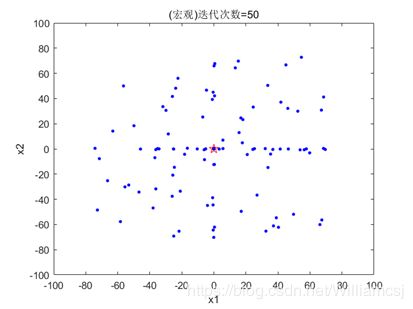
图3.6.1.2 粒子分布(微观)
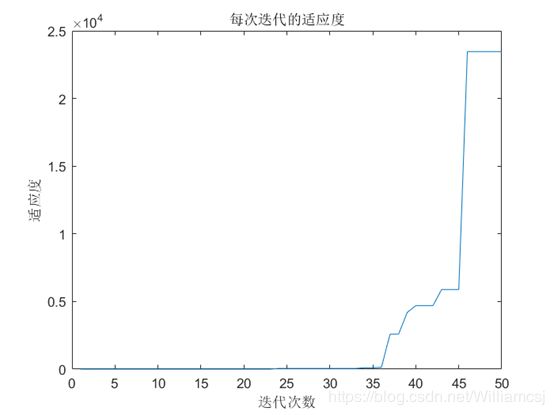
图3.6.1.3 每次迭代的适应度

3.6.2 Vmax=1,Vmin= - 1
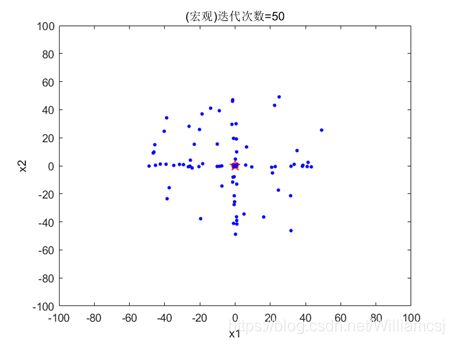
图3.6.2.1 粒子分布(宏观)
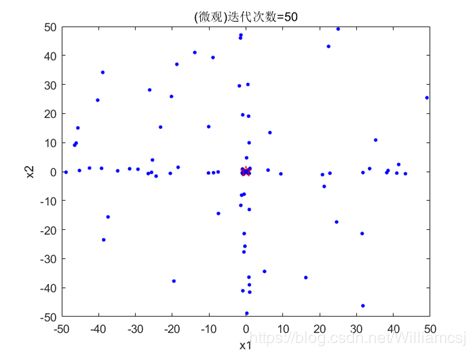
图3.6.2.2 粒子分布(微观)

图3.6.2.3 每次迭代的适应度

3.6.3 Vmax=3,Vmin= - 3
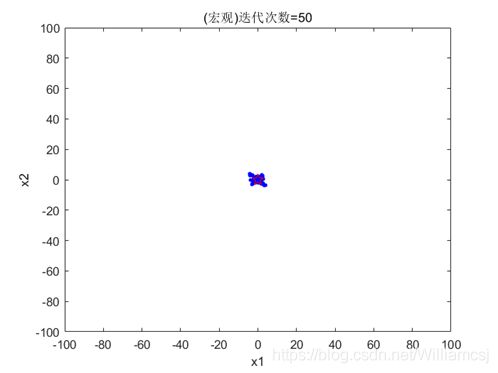
图3.6.3.1 粒子分布(宏观)
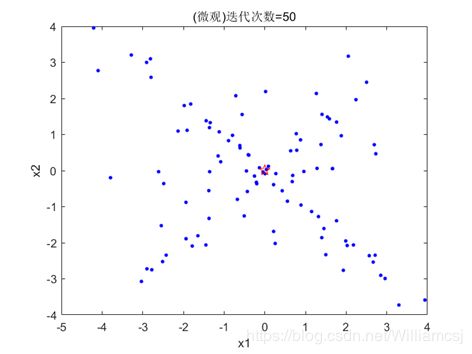
图3.6.3.2 粒子分布(微观)
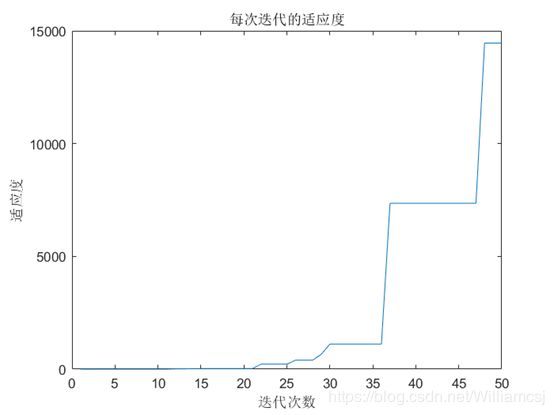
图3.6.3.3 每次迭代的适应度

3.6.4 Vmax=4,Vmin= - 4
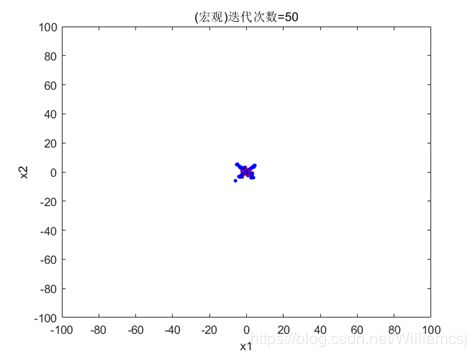
图3.6.4.1 粒子分布(宏观)
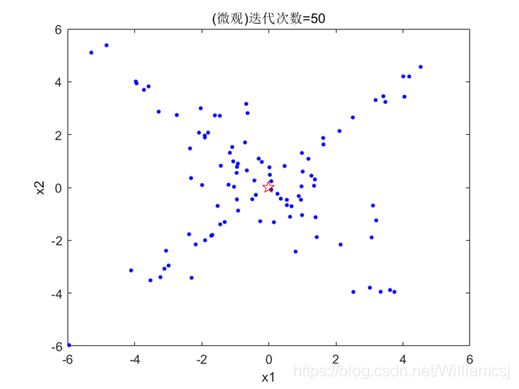
图3.6.4.2 粒子分布(微观)
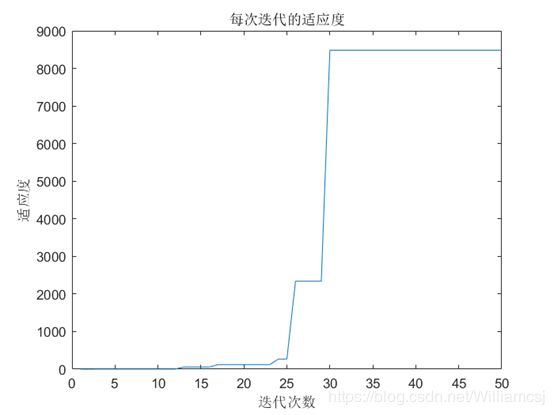
图3.6.4.3 每次迭代的适应度

3.6.5总结
通过以上的实验,我们可以发现,当在这种初始条件下且只改变了最大最小速度时,当速度的幅值的增大,最优适应度先出现增后减,在速度幅值为2的左右(Vmax=2,Vmin= - 2),最优适应度达到最大。显然速度要在一定的范围内,这样才能更接近最优适应度。
3.7优参数带入的的结果
通过上面的分析,我们选出了一组优的参数。惯性权重因子w = 0.3;认知权重因子c1 = 1.5;社会权重因子c2 = 2.0;迭代次数maxgen = 200;粒子移动最大速度Vmax = 2; 最小速度Vmin = -2。
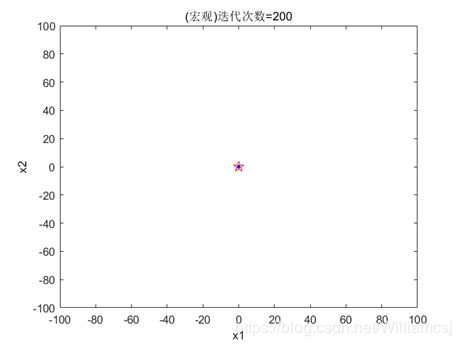
图3.7.1 粒子分布(宏观)
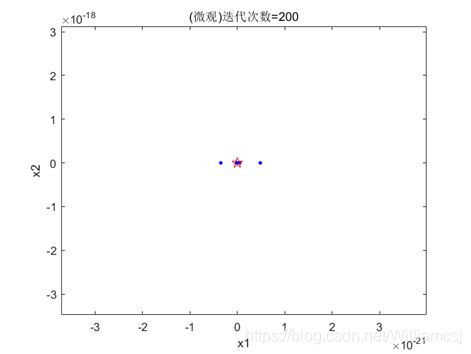
图3.7.2 粒子分布(微观)
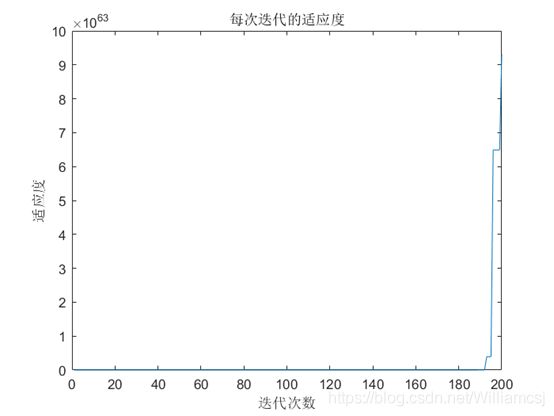
图3.7.3 每次迭代的适应度

4粒子群算法的程序源码(MATLAB)
4.1 主函数
%%
%函数功能:该函数是对运用粒子群算法(PSO)问题求解的
%
%修改函数说明:
% 1.确定维度,不同问题涉及不同的维度
% Dim = 2; %维度(自变量的个数)
% 2.测试函数的修改或者自定义
% index=1; %测试函数索引(对应表里面的函数)
% 3.适应度的与函数结果的关系。
% 若值越小,适应度越大,则不需要用1/,否则反之。
% record(1,i)=1/fitnessgbest; %采取1/fitnessgbest是因为我们设定了值越小,适应度越大。
% fprintf('第%d迭代: \n 最优解:x1 = %f ,x2 = %f \n 全局最佳适应度值:%f\n'...
% ,i,gbest(1),gbest(2),1/fitnessgbest); %输出结果,采取1/fitnessgbest是因为我们设定了值越小,适应度越大。
%
%%
clc;clear;close all;
Dim = 2; %维度(自变量的个数)
index=1; %测试函数索引(对应表里面的函数)
w = 0.3; %惯性权重因子1
c1 = 1.5; %认知权重因子1.5
c2 = 2.0; %社会权重因子1.5
maxgen = 200; %迭代次数50
sizepop = 100; %种群规模100
Vmax = 2; %粒子移动最大速度2
Vmin = -2; %粒子移动最小速度-2
popmax = 100; %自变量最大取值
popmin = -100; %自变量最小取值
record=zeros(1,maxgen);
%% 产生初始粒子和速度
for i = 1:sizepop
% 随机产生一个种群
pop(i,:) = (popmax-popmin)*rand(1,Dim)+popmin; %初始种群
V(i,:) = (Vmax-Vmin)*rand(1,Dim)+Vmin; %初始化速度
% 计算适应度
fitness(i) = fun(pop(i,:),index); %计算适应度(这里设定的是结果的值越小=适应度越低)
end
%% 个体极值和群体极值
[bestfitness bestindex] = min(fitness); %bestindex:全局最优粒子索引
gbest = pop(bestindex,:); %全局最佳位置
pbest = pop; %个体最佳
fitnesspbest = fitness; %个体最佳适应度值
fitnessgbest = bestfitness; %全局最佳适应度值
%% 迭代寻优
for i = 1:maxgen %代数更迭
for j = 1:sizepop %遍历个体
% 速度更新
V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:));
%速度边界处理
V(j,find(V(j,:)>Vmax)) = Vmax;
V(j,find(V(j,:)<Vmin)) = Vmin;
% 种群更新
pop(j,:) = pop(j,:) + V(j,:);
%位置边界处理
pop(j,find(pop(j,:)>popmax)) = popmax;
pop(j,find(pop(j,:)<popmin)) = popmin;
% 适应度值更新
fitness(j) = fun(pop(j,:),index);
end
for j = 1:sizepop
% 个体最优更新
if fitness(j) < fitnesspbest(j)
pbest(j,:) = pop(j,:);
fitnesspbest(j) = fitness(j);
end
% 群体最优更新
if fitness(j) < fitnessgbest
gbest = pop(j,:);
fitnessgbest = fitness(j);
end
end
record(1,i)=1/fitnessgbest; %采取1/fitnessgbest是因为我们设定了值越小,适应度越大。
fprintf('第%d迭代: \n 最优解:x1 = %f ,x2 = %f \n 全局最佳适应度值:%f\n'...
,i,gbest(1),gbest(2),1/fitnessgbest); %输出结果,采取1/fitnessgbest是因为我们设定了值越小,适应度越大。
% 收敛动图绘制存储
% plot(pop(:,1),pop(:,2),'*b')
% axis([popmin popmax popmin popmax])
figure(1)
plot(pop(:,1),pop(:,2),'.b',gbest(1),gbest(2),'rp','MarkerSize',10)
axis([popmin popmax popmin popmax])
x1=xlabel('x1');
x2=ylabel('x2');
title(['(宏观)迭代次数=' num2str(i)]);
% plot3(pop(:,1),pop(:,2),pop(:,3),'*b') %自变量3维 或者 自变量两维加上结果的一维,用于画3维图
% axis([popmin popmax popmin popmax popmin popmax])
figure(2)
plot(pop(:,1),pop(:,2),'.b',gbest(1),gbest(2),'rp','MarkerSize',10)
pause(0.1)
x1=xlabel('x1');
x2=ylabel('x2');
title(['(微观)迭代次数=' num2str(i)]);
drawnow;
frame = getframe(1);
im = frame2im(frame);
[A,map] = rgb2ind(im,256);
if i == 1
imwrite(A,map,'E:\测试图\标准PSO.gif','gif','LoopCount',Inf,'DelayTime',0.1);
else
imwrite(A,map,'E:\测试图\标准PSO.gif','gif','WriteMode','append','DelayTime',0.1);
end
end
%% 适应度值变化绘图
figure(3)
plot(record);
xlabel('迭代次数');
ylabel('适应度');
title('每次迭代的适应度');
4.2 fun函数
function y=fun(x,index)
% x代表参数,index代表测试的函数的选择
% 该测试函数为通用测试函数,可以移植
% 目录
% 函数名 位置 最优值
% 1.Sphere 0 0
% 2.Camel 多个
% 3.Rosenbrock
switch index
case 1 %Sphere函数
y=sum(x.^2);
case 2 %Camel函数,Dim只能取2
if length(x)>2
error('x的维度超出了2');
end
xx=x(1);yy=x(2);y=(4-2.1*xx^2+xx^4/3)*xx^2+xx*yy+(-4+4*yy^2)*yy^2;
case 3 %Rosenbrock函数
y=0;
for i=2:length(x)
y=y+100*(x(i)-x(i-1)^2)^2+(x(i-1)-1)^2;
end
case 4 %Ackley函数
a = 20; b = 0.2; c = 2*pi;
s1 = 0; s2 = 0;
for i=1:length(x)
s1 = s1+x(i)^2;
s2 = s2+cos(c*x(i));
end
y = -a*exp(-b*sqrt(1/length(x)*s1))-exp(1/length(x)*s2)+a+exp(1);
case 5 %Rastrigin函数
s = 0;
for j = 1:length(x)
s = s+(x(j)^2-10*cos(2*pi*x(j)));
end
y = 10*length(x)+s;
case 6 %Griewank函数
fr = 4000;
s = 0;
p = 1;
for j = 1:length(x); s = s+x(j)^2; end
for j = 1:length(x); p = p*cos(x(j)/sqrt(j)); end
y = s/fr-p+1;
case 7 %Shubert函数
s1 = 0;
s2 = 0;
for i = 1:5
s1 = s1+i*cos((i+1)*x(1)+i);
s2 = s2+i*cos((i+1)*x(2)+i);
end
y = s1*s2;
case 8 %beale函数
y = (1.5-x(1)*(1-x(2)))^2+(2.25-x(1)*(1-x(2)^2))^2+(2.625-x(1)*(1-x(2)^3))^2;
case 9 %Schwefel函数
s = sum(-x.*sin(sqrt(abs(x))));
y = 418.9829*length(x)+s;
case 10 %Schaffer函数
temp=x(1)^2+x(2)^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
otherwise
disp('no such function, please choose another');
end