2020网易笔试编程题（三）

题目：现在有n个物品，每一个物品都有一个价值，现在想将这些物品分给两个人，要求这两个人每一个人分到的物品价值总和相同（个数可以不同，总价值相同即可），剩下的物品就需要扔掉，现在想知道最少需要扔多少价值的物品才能满足要求分给两个人。
输入输出：一行输入一个整数n，代表物品的个数。接下来输入n个数，a[i]表示第i个物品的价值。输出一个数表示最少需要扔掉的价值。
个人思路：这题简单来说就是求最优解，使用动态规划的思想是没跑了，奈何本人动态规划算法学的太菜，花了近一天的时间，找了几道动态规划的题，调试多种各自特殊的情况才写出自认为完整的代码（应该是没有错的了）。唉，只能说工作真是不好找，算法题简直要命！
一、吐槽完毕，来说正题。要求扔掉的物品总价值最少，反过来其实就是求分配的物品总价值最多，并且要能够平分总价值给两人，也就是两人每个人得到的物品价值总和相同，物品数量无所谓。举例来说：加入有7个物品，价值分别为{12,5,30,25,33,10,18}，经过计算可得最少要扔掉17价值的物品，即5和12，剩余的刚好可以分为{25,33}和{10,18,30}，各58的价值，平分给两人。
二、我一开始的想法是将物品价值从小到大排序，然后从价值最小的开始剔除，先计算当前未剔除的物品总价值，然后除以2，再从未剔除的物品中寻找是否存在几个物品的价值总和等于除以2后的价值，如果存在，就不用再剔除了，之前剔除的就是最小的了；如果不存在，就继续剔除一个当前价值最小的物品，再进行判断，依此类推，直到求出结果。
三、初步的大体思路就是这样，那么首先要解决的就是如何判断未剔除的物品中是否存在几个物品的价值总和等于除以2后的价值。我们可以把这个问题看作是在一堆数中寻找和为定值的任意多个数，即判断是否存在几个数的和为指定的数。这个我参考了寻找和为定值的任意多个数这篇博客，方法很多，我选的是递归的方法。因为参考的博客是求所有种可能的组合，而我只需要进行判断，即只要找到一种组合，该组合中的数加起来等于指定的值，就符合要求，不需要求出所有种可能，计算时间没有他那么多，因此经过改良，符合本题的判断函数代码定义如下所示，函数的输入参数为物品的个数n，物品的价值集合p[n]，以及当前价值总和的一半Sum，因为题目要求中没说明价值是否为整型，所有就定义为了double型。

int k = 0;
bool SumCheck(int n, double p[], double Sum) {
	bool flag;
	if (n <= 0 || Sum < 0)
		return false;
	if (k > 0)
	{
		if (Sum == p[n - 1])
			return true;
	}
	//考虑取第n个数
	k++;
	flag = SumCheck(n - 1, p, Sum - p[n - 1]);
	if (flag)
		return true;
	//不考虑取第n个数
	k--;
	flag = SumCheck(n - 1, p, Sum);
	if (flag)
		return true;
	return false;
}

四、判断当前物品的总价值是否能平分已经实现了，接下来就是依次剔除物品并判断的过程了。但是，我上面说了那是我的初步想法，之后经过思考发现漏洞很多！因为我是从最小价值的物品开始剔除的，万一实际要剔除的不包括最小价值的物品呢？以{10,12,18,25,30,33}为例，经过计算可得最少扔掉的物品价值应为12，而不是最小的10，因为扔掉10后明显无法平分，因此需要改进思路。经过一番思考，我依旧是从上面那个方法中得到了思路，上面判断是否存在几个数和为指定值的核心思路就是：考虑是否取第n个数，问题可以转化为前n-1个数和为Sum-p[n-1]的问题，也可以转化为后n-1个数的求和问题。使用递归思想解决。（1.如果取第n个数，即求得前n-1个数满足和为Sum-p[n-1]的问题；2.如果不取第n个数，即求得前n-1个数满足和为Sum的问题）。 显然他的思路就考虑到了两种情况，转化为我们的问题就是考虑是否扔掉第i个物品，如何考虑扔掉，就减去它的价值，然后递归判段剩下的物品；如果不考虑扔掉，就不减去它的价值，然后依旧递归判断扔掉下一个物品后是否可行，一直递归到剩余的总价值可平分。
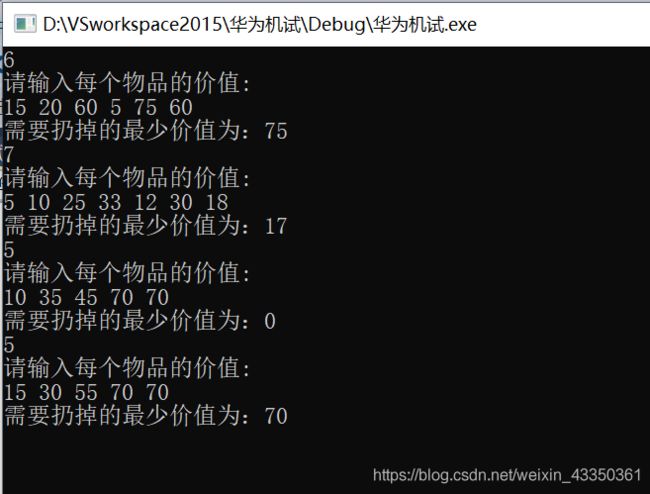
五、思路基本已经确定好了，代码基本就也能得出来了，然而经过不同的例子调试，发现还是存在者一些特殊情况没考虑到。例如，{5,15,20,60,60,75}，如果直接按照上述思路来解决，结果就是扔掉的价值为5+20+60=85，而实际上扔掉的最少价值应该是75，也就是说上述方法没有考虑有多种解的情况。经过一番思考，本人目前能想到的方法就是用动态数组存储多种解的值，然后进行比较，找出最小的解即为最少的扔掉价值。
代码如下所示，具体就不详细解释了，可以看注释，个人感觉我的这种方法也不是最优解法，时间复杂度和空间复杂度都明显偏高，希望有大神能给出更好的解法，啾咪！

#include
#include
#include
using namespace std;
double SumPrice = 0.0; //定义全局变量记录初始所有物品的总价值
vector<double> result; //记录可能存在的多个解
int k = 0;

//判断数组中是否存在几个数的和等于指定的Sum
bool SumCheck(int n, double p[], double Sum) {
	bool flag;
	if (n <= 0 || Sum < 0)
		return false;
	if (k > 0)
	{
		if (Sum == p[n - 1])
			return true;
	}
	//考虑取第n个数
	k++;
	flag = SumCheck(n - 1, p, Sum - p[n - 1]);
	if (flag) //如果找到，就不进行下一步
		return true;
	//不考虑取第n个数
	k--;
	flag = SumCheck(n - 1, p, Sum);
	if (flag)
		return true;
	return false;
}
//求最少扔掉的物品的价值
double MinPriceToThrow(int n, double p[],int m, double CurrentSum) {
	int MinPrice;
	if (m >= n)
		return -1; //如果递归到最后还不能平分，就返回-1，说明无法平分
	double halfPrice= CurrentSum / 2.0;
	k = 0;
	if (SumCheck(n, p, halfPrice)) //判断当前价值是否能平分
		return SumPrice - CurrentSum; //可以平分就返回需要扔掉的物品总价值
	int temp = p[m];
	//考虑扔掉第m个物品，则把第m个物品的价值置0，再从当前总价值中减去，算作扔掉
	p[m] = 0;
	MinPrice = MinPriceToThrow(n, p, m + 1, CurrentSum - temp);
	if (MinPrice != -1)
		result.push_back(MinPrice); //如果得到了可以扔掉的价值，存储进数组中	 
	//不考虑扔掉第m个物品，则把第m个物品的价值复原，并且不从总价值中减去
	p[m] = temp;
	MinPrice = MinPriceToThrow(n, p, m + 1, CurrentSum);
	if (MinPrice != -1)
		result.push_back(MinPrice);
	if (result.size() >= 1)
	{   //如果有多个解，则返回最小的那个解
		sort(result.begin(), result.end()); 
		return result[0];
	}
	return MinPrice;
}

int main()
{
	int n;
	double price;	
	while (cin >> n) {
		SumPrice = 0.0; //全局变量每轮新的计算都要初始化为0
		result.clear(); //数组也是需要清空
		double *p = new double[n];
		cout << "请输入每个物品的价值:" << endl;
		for (int i = 0; i < n; ++i) {
			cin >> price;
			p[i] = price;
			SumPrice += p[i]; //计算所有物品的总价值
		}
		sort(p, p + n); //从小到大排序
		cout <<"需要扔掉的最少价值为："<< MinPriceToThrow(n, p, 0, SumPrice) << endl;
	}
	system("pause");
	return 0;
}

运行结果如下所示：