懒人终于开始写博客啦！~~~撒花~~~
这两天集中做了一下历届noip的搜索，还是很有收获的，所以整理成一篇文章。自认为是按照难度从小到大做的QWQ
1565: NOIP2004 虫食算
时间限制: 1 Sec
内存限制: 128 MB
提交: 18
解决: 5
题目描述
所谓虫食算，就是原先的算式中有一部分被虫子啃掉了，需要我们根据剩下的数字来判定被啃掉的字母。来看一个简单的例子：
43#98650#45
+ 8468#6633
44445506978
其中#号代表被虫子啃掉的数字。根据算式，我们很容易判断：第一行的两个数字分别是5和3，第二行的数字是5。
现在，我们对问题做两个限制：
首先，我们只考虑加法的虫食算。这里的加法是N进制加法，算式中三个数都有N位，允许有前导的0。
其次，虫子把所有的数都啃光了，我们只知道哪些数字是相同的。我们将相同的数字用相同的字母表示，不同的数字用不同的字母表示。如果这个算式是N进制的，我们就取英文字母表中的前N个大写字母来表示这个算式中的0到N-1这N个不同的数字（但是这N个字母并不一定顺序地代表0到N-1）。输入数据保证N个字母分别至少出现一次。
BADC
+ CBDA
DCCC
上面的算式是一个4进制的算式。很显然，我们只要让ABCD分别代表0123，便可以让这个式子成立了。你的任务是，对于给定的N进制加法算式，求出N个不同的字母分别代表的数字，使得该加法算式成立。输入数据保证有且仅有一组解。
输入
包含4行。第一行有一个正整数N（N <= 26），后面的3行每行有一个由大写字母组成的字符串，分别代表两个加数以及和。这3个字符串左右两端都没有空格，从高位到低位，并且恰好有N位。
输出
包含一行。在这一行中，应当包含唯一的那组解。解是这样表示的：输出N个数字，分别表示A，B，C……所代表的数字，相邻的两个数字用一个空格隔开，不能有多余的空格。
样例输入
5
ABCED
BDACE
EBBAA
样例输出
1 0 3 4 2
提示
对于30%的数据，保证有N <= 10；
对于50%的数据，保证有N <= 15；
对于全部的数据，保证有N <= 26。
对于30%的数据，保证有N <= 10；
对于50%的数据，保证有N <= 15；
对于全部的数据，保证有N <= 26。
这个时候我好像还没有写过任何爆搜....于是当时我的思路是这样的： 考虑进位！要剪枝！没了
于是冷静下来整理出这样几个主要的点 首先剪枝【以下所有的东西都要考虑进位】1.如果我们搜到某一位 三个数都搜到了但是出现矛盾剪枝 2.某一位已经搜到了两个数 但是所有有能对的第三个数已经被占用 剪枝 然后就没有了。。。高能预警：前方有长代码
其实就是我不会写搜索。。。于是我讨论了每个数是否出现的情况。。。算了上代码
#include
#include
#include
#include
#include
using namespace std;
int n,ci[30],di[30],fi[30],pos[30],cnt;
char ch[30];
bool use[30],v[30];
bool check()
{
for(int i=0;i=n) r=1;
else r=0;
dfs(x-1,r);
}
else
{
if(use[t]) return ;
use[t]=1;
pos[fi[x]]=t;
if(pos[ci[x]]+pos[di[x]]+lef>=n) r=1;
else r=0;
v[fi[x]]=1;
dfs(x-1,r);
v[fi[x]]=0;
use[t]=0;
}
}
else if(v[ci[x]])
{
if(v[fi[x]])
{
int t=(pos[fi[x]]+n-pos[ci[x]]-lef)%n;
if(use[t]) return ;
else
{
use[t]=1;
pos[di[x]]=t;
if(pos[ci[x]]+pos[di[x]]>pos[fi[x]]) r=1;
else r=0;
v[di[x]]=1;
dfs(x-1,r);
v[di[x]]=0;
use[t]=0;
}
}
else
{
for(int i=n-1;i>=0;i--)
if(!use[i])
{
int t=(pos[ci[x]]+i+lef)%n;
if(use[t]&&t!=i) continue;
use[i]=1;
use[t]=1;
pos[di[x]]=i; pos[fi[x]]=t;
if(pos[ci[x]]+pos[di[x]]+lef>=n) r=1;
else r=0;
v[di[x]]=1; v[fi[x]]=1;
dfs(x-1,r);
use[i]=0;
v[di[x]]=0; v[fi[x]]=0; use[t]=0;
}
}
}
else if(v[di[x]])
{
if(v[fi[x]])
{
int t=(pos[fi[x]]+n-pos[di[x]]-lef)%n;
if(use[t]) return ;
else
{
use[t]=1;
pos[ci[x]]=t;
if(pos[ci[x]]+pos[di[x]]>pos[fi[x]]) r=1;
else r=0;
v[ci[x]]=1;
dfs(x-1,r);
use[t]=0;
v[ci[x]]=0;
}
}
else
{
for(int i=n-1;i>=0;i--)
if(!use[i])
{
pos[ci[x]]=i;
int t=(pos[ci[x]]+pos[di[x]]+lef)%n;
pos[fi[x]]=t;
if(use[t]&&t!=i) continue;
use[i]=1; use[t]=1;
if(pos[ci[x]]+pos[di[x]]+lef>=n) r=1;
else r=0;
v[ci[x]]=1; v[fi[x]]=1;
dfs(x-1,r);
use[i]=0; use[t]=0;
v[ci[x]]=0; v[fi[x]]=0;
}
}
}
else
{
for(int i=n-1;i>=0;i--)
{
if(!use[i])
{
pos[ci[x]]=i;
use[i]=1;
v[ci[x]]=1;
for(int j=n-1;j>=0;j--)
if(!use[j]||(use[j]&&di[x]==ci[x]))
{
pos[di[x]]=j;
use[j]=1;
v[di[x]]=1;
int t=(pos[ci[x]]+pos[di[x]]+lef)%n;
if(v[fi[x]])
{
if(t!=pos[fi[x]]) {use[j]=0; v[di[x]]=0; continue ;}
if(pos[ci[x]]+pos[di[x]]+lef>=n) r=1;
else r=0;
dfs(x-1,r);
}
else
{
if(use[t]&&j!=t) {use[j]=0; v[di[x]]=0; continue ;}
else if(j!=t||(j==t&&fi[x]==di[x]))
{
pos[fi[x]]=(t%n);
use[t]=1;
if(pos[ci[x]]+pos[di[x]]+lef>=n) r=1;
else r=0;
v[fi[x]]=1;
dfs(x-1,r);
v[fi[x]]=0;
use[t]=0;
}
}
use[j]=0;
v[di[x]]=0;
}
use[i]=0;
v[ci[x]]=0;
}
}
}
}
}
int main()
{
cin>>n;
scanf("%s",ch);
for(int i=0;i
为什么觉得这个CSDN的格式看着这么丑呢QAQ 【我就不说我代码写得丑】
1620: NOIP2011 Mayan游戏
时间限制: 5 Sec
内存限制: 128 MB
提交: 28
解决: 5
题目描述
Mayan puzzle 是最近流行起来的一个游戏。游戏界面是一个 7行 5 列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：
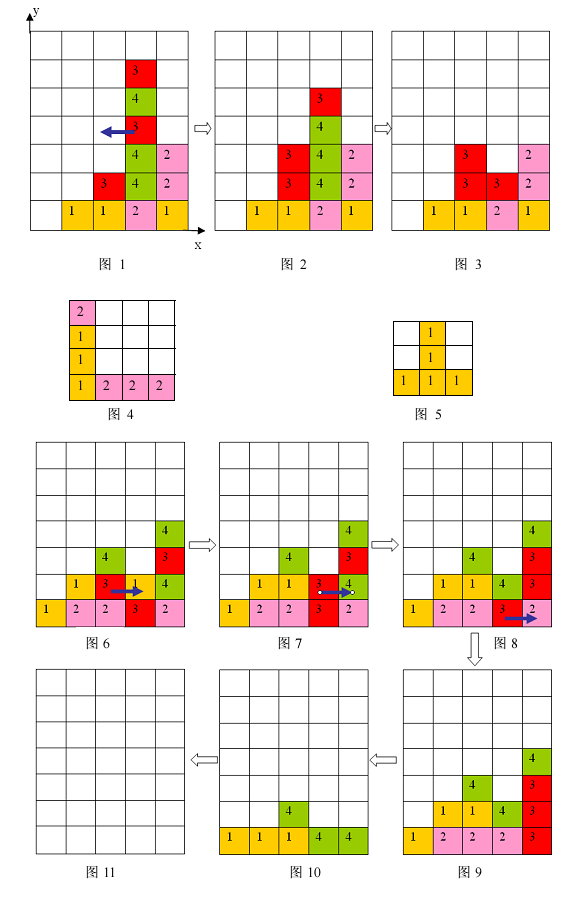
1、 每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图 6 到图 7）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图 1 和图2）；
2、 任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图 1 到图3）。
注意：
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图 4，三个颜色为 1 的方块和三个颜色为 2 的方块会同时被消除，最后剩下一个颜色为 2 的方块）。
b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图 5 所示的情形，5 个方块会同时被消除）。
3、 方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。
上面图 1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0），将位于（3, 3）的方块向左移动之后，游戏界面从图 1 变成图 2 所示的状态，
此时在一竖列上有连续三块颜色为 4 的方块，满足消除条件，消除连续 3块颜色为 4的方块后，上方的颜色为 3 的方块掉落，形成图 3 所示的局面。
输入
输入文件共 6行。
第一行有一个整数n，表示要求游戏通关的步数。
接下来的 5行，描述 7*5 的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个 0 结束，自下向上表示每竖列方块的颜色编号（颜色不多于 10 种，从 1 开始顺序编号，相同数字表示相同颜色）。
输入数据保证初始棋盘中没有可以消除的方块。
输出
如果有解决方案，输出 n 行，每行包含 3 个整数x，y，g，表示一次移动，每两个整数之间用一个空格隔开，其中（x，y）表示要移动的方块的坐标，g 表示移动的方向，1 表示向右移动，-1 表示向左移动。注意：多组解时，按照 x 为第一关健字，y 为第二关键字，1优先于-1，给出一组字典序最小的解。游戏界面左下角的坐标为（0，0）。
如果没有解决方案，输出一行，包含一个整数-1。
这个搜索我写的真的是很差。。。跑了4s多
这个主要的剪枝：
1.如果两个相邻位置都是方块 我们只交换一次
2.如果两个方块颜色一样 我们不交换
3.如果某个颜色的剩余少于3个 可以剪枝
然后我调了好久啊 我们真的要好好看题 如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除
我就是没有注意这个 以为只要三个联通就可以消除 然后WAWAWAWAWAWAWAWA
高能预警：前方有长代码
好了这个自认为写得不怎么样QAQ
#include
#include
#include
#include
#include
using namespace std;
int mp[8][8],n,colnum,num[11];
int lst[8][8][6],col[11][8];
int xx[10],yy[10],s[10];
bool ins(int x,int y){return x>0&&x<=7&&y>0&&y<=5;}
bool check(int x,int y,int dep)
{
if(!ins(x,y)||!ins(x,y+1)) return false;
return (lst[x][y][dep]&&!lst[x][y+1][dep]||lst[x][y][dep]!=lst[x][y+1][dep]&&lst[x][y][dep]);
}
bool check2(int x,int y,int dep)
{
return (lst[x][y][dep]&&!lst[x][y-1][dep]&&ins(x,y)&&ins(x,y-1));
}
int cal(int dep)
{
int minn=100;
for(int i=1;i<=colnum;i++)
if(col[i][dep]) minn=min(minn,col[i][dep]);
return minn;
}
int sx[40],sy[40],h,t;
int wx[5]={0,0,1,-1},wy[5]={1,-1,0,0};
int v[10][10],T;
bool hang,lie,xiao[8][6];
bool ok(int x,int y)
{
hang=0,lie=0;
T++;
int c=mp[x][y];
if(c==0) return false;
h=t=0;
sx[++t]=x; sy[t]=y;
v[x][y]=T;
while(h!=t)
{
int nx=sx[++h],ny=sy[h];
for(int i=0;i<2;i++)
{
int dx=nx+wx[i],dy=ny+wy[i];
if(!ins(dx,dy)||mp[dx][dy]!=c||v[dx][dy]==T) continue;
sx[++t]=dx,sy[t]=dy,v[dx][dy]=T;
}
if(h>=3) return 1;
}
T++;
h=t=0;
sx[++t]=x; sy[t]=y;
v[x][y]=T;
while(h!=t)
{
int nx=sx[++h],ny=sy[h];
for(int i=2;i<4;i++)
{
int dx=nx+wx[i],dy=ny+wy[i];
if(!ins(dx,dy)||mp[dx][dy]!=c||v[dx][dy]==T) continue;
sx[++t]=dx,sy[t]=dy,v[dx][dy]=T;
}
if(h>=3) return 1;
}
return false;
}
void fill()
{
for(int i=1;i<=7;i++)
for(int j=1;j<=5;j++)
if(xiao[i][j])
{
num[mp[i][j]]--;
mp[i][j]=0;
}
}
bool xc()
{
bool flag=0;
memset(xiao,0,sizeof xiao);
for(int i=1;i<=7;i++)
for(int j=1;j<=5;j++)
if(ok(i,j)) flag=1,xiao[i][j]=1;
if(flag) fill();
return flag;
}
void falling()
{
for(int j=1;j<=5;j++)
{
for(int i=1;i<=7;i++)
if(!mp[i][j])
{
int p=0;
while(!mp[i+p][j]&&p+i<=7) p++;
for(int l=i;l+p<=7;l++)
mp[l][j]=mp[l+p][j],mp[l+p][j]=0;
}
}
}
int numa=0;
void mov(int x,int y,int dep,int o)
{
xx[dep]=x; yy[dep]=y;
for(int i=1;i<=7;i++)
for(int j=1;j<=5;j++)
mp[i][j]=lst[i][j][dep];
for(int i=1;i<=colnum;i++)
num[i]=col[i][dep];
if(o==0) swap(mp[x][y],mp[x][y+1]);
else swap(mp[x][y],mp[x][y-1]);
falling();
while(xc()) falling();
for(int i=1;i<=7;i++)
for(int j=1;j<=5;j++)
lst[i][j][dep+1]=mp[i][j];
for(int i=1;i<=colnum;i++)
col[i][dep+1]=num[i];
}
bool pty()
{
for(int i=1;i<=colnum;i++)
if(num[i]) return false;
return true;
}
void print()
{
for(int i=0;i
1605: NOIP2009 靶形数独
时间限制: 2 Sec
内存限制: 128 MB
提交: 11
解决: 4
题目描述
小城和小华都是热爱数学的好学生，最近，他们不约而同地迷上了数独游戏，好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了，于是他们向
Z博士请教，Z博士拿出了他最近发明的“靶形数独”，作为这两个孩子比试的题目。
靶形数独的方格同普通数独一样，在9格宽×9格高的大九宫格中有9个3格宽×3格高的小九宫格（用粗黑色线隔开的）。在这个大九宫格中，有一些数字是已知的，根据这些数字，利用逻辑推理，在其他的空格上填入1到9的数字。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。但靶形数独有一点和普通数独不同，即每一个方格都有一个分值，而且如同一个靶子一样，离中心越近则分值越高。（如图）
上图具体的分值分布是：最里面一格（黄色区域）为10分，黄色区域外面的一圈（红色区域）每个格子为9分，再外面一圈（蓝色区域）每个格子为8分，蓝色区域外面一圈（棕色区域）每个格子为7分，最外面一圈（白色区域）每个格子为6分，如上图所示。比赛的要求是：每个人必须完成一个给定的数独（每个给定数独有可能有不同的填法），而且要争取更高的总分数。而这个
总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。如图，在以下这个已经填完数字的靶形数独游戏中，总分为2829。游戏规定，将以总分数的高低决出胜负。
由于求胜心切，小城找到了善于编程的你，让你帮他求出，对于给定的靶形数独，能够得到的最高分数。
输入
一共9行，每行9个整数（每个数都在0—9的范围内），表示一个尚未填满的数独方格，未填满的空格用“0”表示。每两个数字之间用一个空格隔开。
输出
输出可以得到的靶形数独的最高分数。如果这个数独无解，则输出整数-1。
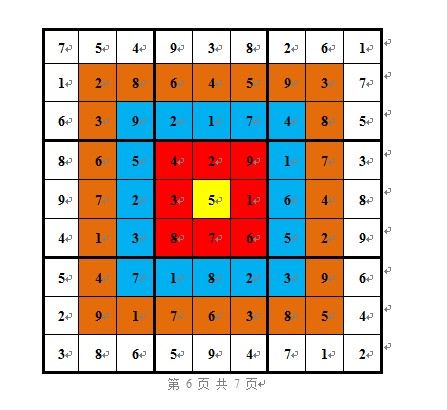
样例输入
7 0 0 9 0 0 0 0 1
1 0 0 0 0 5 9 0 0
0 0 0 2 0 0 0 8 0
0 0 5 0 2 0 0 0 3
0 0 0 0 0 0 6 4 8
4 1 3 0 0 0 0 0 0
0 0 7 0 0 2 0 9 0
2 0 1 0 6 0 8 0 4
0 8 0 5 0 4 0 1 2
样例输出
2829
提示
40%的数据，数独中非0数的个数不少于30。
80%的数据，数独中非0数的个数不少于26。
100%的数据，数独中非0数的个数不少于24。
这个。。。不好意思我搜题解了。。。因为最开始加了一个弱弱的剪枝然后就next_permutation 样例跑了15s...所以我就义无反顾的。。。搜了题解【请忽略博主的语文水平】
然后我发现位运算这个东西真是非常巧妙啊！O(∩_∩)O
首先我们在输入之后排序 从缺数少的行先搜 这样应该会更优一点（...）
然后我们记录三个数组分别表示 每行 每列 每个3*3格子的数字使用情况 位运算好啊 妙不可言啊 所以上代码吧
#include
#include
#include
#include
#include
using namespace std;
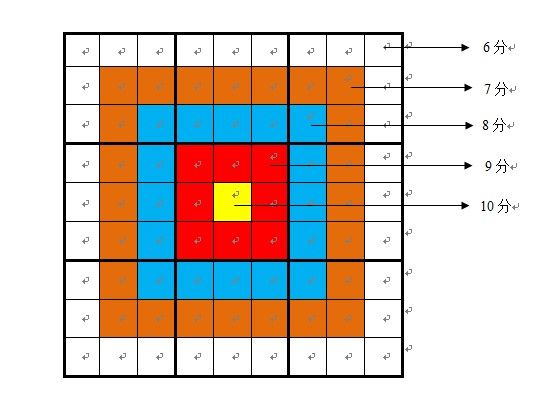
int score[10][10]=
{
0,0,0,0,0,0,0,0,0,0,
0,6,6,6,6,6,6,6,6,6,
0,6,7,7,7,7,7,7,7,6,
0,6,7,8,8,8,8,8,7,6,
0,6,7,8,9,9,9,8,7,6,
0,6,7,8,9,10,9,8,7,6,
0,6,7,8,9,9,9,8,7,6,
0,6,7,8,8,8,8,8,7,6,
0,6,7,7,7,7,7,7,7,6,
0,6,6,6,6,6,6,6,6,6,
} ;
int mp[10][10],z[10],h[110],e[3][3],k[10],st[10],num[10],ans;
int cal()
{
int res=0;
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++)
res+=mp[i][j]*score[i][j];
return res;
}
void dfs(int x) // z[i]和h[j]
{
if(x==10)
{
ans=max(ans,cal());
return ;
}
else
{
int i,pos,p,j,xx,s;
i=st[x]; //表示当前搜索的行
pos=(1<<9)-1-k[i]; //表示当前行的空白列
p=pos&-pos; //表示第一个空白列
k[i]|=p; //把这位填上
j=(int)log2(p)+1; //缺少位的二进制表示
xx=(1<<9)-1-(z[i]|h[j]|e[(i-1)/3][(j-1)/3]);
while(xx>0)
{
s=xx&-xx;
xx-=s;
mp[i][j]=(int)log2(s)+1;
z[i]|=s;
h[j]|=s;
e[(i-1)/3][(j-1)/3]|=s;
if(pos==p) dfs(x+1);
else dfs(x);
z[i]-=s;
h[j]-=s;
e[(i-1)/3][(j-1)/3]-=s;
}
k[i]-=p;
}
}
int main()
{
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++)
{
scanf("%d",&mp[i][j]);
if(mp[i][j])
{
k[i]|=(1<<(j-1));
int p=(1<<(mp[i][j]-1));
if((p&z[i])||(p&h[j])||(p&e[(i-1)/3][(j-1)/3])) {cout<<-1; return 0;}
z[i]|=p;
h[j]|=p;
e[(i-1)/3][(j-1)/3]|=p;
}
else num[i]++;
}
for(int i=1;i<=9;i++) st[i]=i;
for(int i=1;i<=9;i++)
for(int j=i+1;j<=9;j++)
if(num[st[i]]>num[st[j]]) swap(st[i],st[j]);
int p=1;
while(num[p]==0) p++;
dfs(p);
if(ans) cout<
这个时候我就有一点颓了。。。于是水了一个八数码【当然也没加什么估价函数】然后简单回忆了一下过去，，，
所以最后还是要鼓起勇气做华容道啊QWQ
1643: NOIP 2013 华容道
时间限制: 1 Sec
内存限制: 128 MB
提交: 43
解决: 5
题目描述
小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：
1. 在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1 个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；
2. 有些棋子是固定的，有些棋子则是可以移动的；
3. 任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。
游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候，空白的格子在第 EXi 行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi
列，目标位置为第 TXi 行第 TYi 列。
假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。
输入
接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。
接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。
输出
输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法
完成目标则输出−1。
样例输入
3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2
样例输出
2
-1
提示
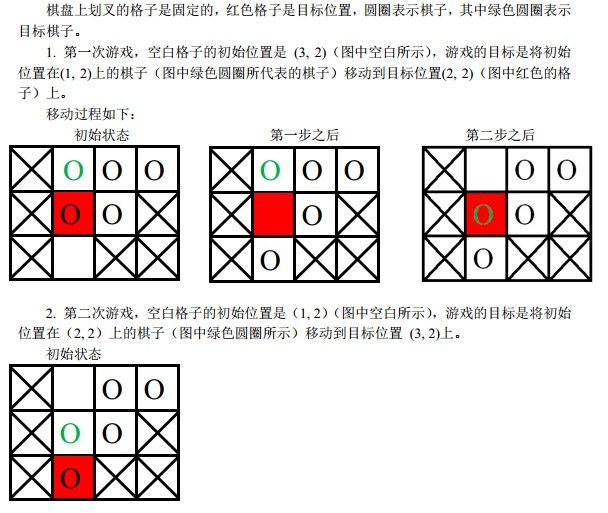
必然是从位置（2， 2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置， 游戏无法完成。
这个ljss神犇第一次讲的时候我没有听懂...于是留下了非常恐怖的印象...
但是还是要鼓起勇气做呀！首先考虑60分做法 就是bfs!然后我们考虑优化 bfs的时间浪费在于一次又一次的搜这张图.所以我们可以想一想能不能提前跑出来。。。
不卖关子了 一个方块移动的条件是 周围有空格 所以列出状态move[i][j][k][l]表示 当前需要移动的块在(i,j)，原来空白块在k方向，预计把空白块移动到j方向的最少步数
解释一下 这里方向表示空白块与当前块相邻 只有上下左右四个方向 然后这个数组我们可以bfs预处理出来 然后注意bfs的时候不能经过当前块
我们给每个位置设置四种状态dis[i][j][k]表示 当前需要移动的块在(i,j)，空白块在其k方向的最小花费。然后我们可以先跑一边bfs确定把空白块移动到起始位置旁边的花费【这里我犯了一个刚写bfs都不会犯的错误导致无限RE】然后把四个状态扔进队列跑spfa
不要连边直接跑！不要连边直接跑！不要连边直接跑！为什么要给自己找麻烦呢
这好像是OI生涯最长代码？如果后来没删除加边还要多好多QAQ
#include
#include
#include
#include
#include
# define inf 0x3f3f3f3f
using namespace std;
int f[5005],q[5005];
int n,m,qq,mp[32][32],mov[32][32][5][5];
int h,t,xx[1005],yy[1005],stp[32][32],wx[4]={-1,1,0,0},wy[4]={0,0,-1,1};
int ob[4]={1,0,3,2},sx,sy,tx,ty,kx,ky;
bool v[5005];
bool ins(int x,int y){return x>0&&x<=n&&y>0&&y<=m;}
void find(int a,int b)
{
mp[a][b]=0;
if(mp[a-1][b])
{
h=t=0;
memset(stp,0,sizeof stp);
xx[++t]=a-1,yy[t]=b;
while(h!=t)
{
int x=xx[++h],y=yy[h];
for(int i=0;i<4;i++)
{
int nx=x+wx[i],ny=y+wy[i];
if(!mp[nx][ny]||!ins(nx,ny)||stp[nx][ny]) continue;
xx[++t]=nx,yy[t]=ny,stp[nx][ny]=stp[x][y]+1;
}
}
if(stp[a+1][b]&&mp[a+1][b]&&ins(a+1,b)) mov[a][b][0][1]=stp[a+1][b];
if(stp[a][b+1]&&mp[a][b+1]&&ins(a,b+1)) mov[a][b][0][3]=stp[a][b+1];
if(stp[a][b-1]&&mp[a][b-1]&&ins(a,b-1)) mov[a][b][0][2]=stp[a][b-1];
}
if(mp[a+1][b])
{
h=t=0;
memset(stp,0,sizeof stp);
xx[++t]=a+1,yy[t]=b;
while(h!=t)
{
int x=xx[++h],y=yy[h];
for(int i=0;i<4;i++)
{
int nx=x+wx[i],ny=y+wy[i];
if(!mp[nx][ny]||!ins(nx,ny)||stp[nx][ny]) continue;
xx[++t]=nx,yy[t]=ny,stp[nx][ny]=stp[x][y]+1;
}
}
if(stp[a-1][b]&&mp[a-1][b]&&ins(a-1,b)) mov[a][b][1][0]=stp[a-1][b];
if(stp[a][b+1]&&mp[a][b+1]&&ins(a,b+1)) mov[a][b][1][3]=stp[a][b+1];
if(stp[a][b-1]&&mp[a][b-1]&&ins(a,b-1)) mov[a][b][1][2]=stp[a][b-1];
}
if(mp[a][b+1])
{
h=t=0;
memset(stp,0,sizeof stp);
xx[++t]=a,yy[t]=b+1;
while(h!=t)
{
int x=xx[++h],y=yy[h];
for(int i=0;i<4;i++)
{
int nx=x+wx[i],ny=y+wy[i];
if(!mp[nx][ny]||!ins(nx,ny)||stp[nx][ny]) continue;
xx[++t]=nx,yy[t]=ny,stp[nx][ny]=stp[x][y]+1;
}
}
if(stp[a+1][b]&&mp[a+1][b]&&ins(a+1,b)) mov[a][b][3][1]=stp[a+1][b];
if(stp[a-1][b]&&mp[a-1][b]&&ins(a-1,b)) mov[a][b][3][0]=stp[a-1][b];
if(stp[a][b-1]&&mp[a][b-1]&&ins(a,b-1)) mov[a][b][3][2]=stp[a][b-1];
}
if(mp[a][b-1])
{
h=t=0;
memset(stp,0,sizeof stp);
xx[++t]=a,yy[t]=b-1;
while(h!=t)
{
int x=xx[++h],y=yy[h];
for(int i=0;i<4;i++)
{
int nx=x+wx[i],ny=y+wy[i];
if(!mp[nx][ny]||!ins(nx,ny)||stp[nx][ny]) continue;
xx[++t]=nx,yy[t]=ny,stp[nx][ny]=stp[x][y]+1;
}
}
if(stp[a+1][b]&&mp[a+1][b]&&ins(a+1,b)) mov[a][b][2][1]=stp[a+1][b];
if(stp[a-1][b]&&mp[a-1][b]&&ins(a-1,b)) mov[a][b][2][0]=stp[a-1][b];
if(stp[a][b+1]&&mp[a][b+1]&&ins(a,b+1)) mov[a][b][2][3]=stp[a][b+1];
}
mp[a][b]=1;
}
int cal(int x,int y,int o) {return (x-1)*m+y+n*m*o;}
void bfs()
{
memset(stp,inf,sizeof stp);
h=t=0;
mp[kx][ky]=0;
mp[sx][sy]=0;
xx[++t]=kx,yy[t]=ky; stp[kx][ky]=0;
while(h!=t)
{
int x=xx[++h],y=yy[h];
for(int i=0;i<4;i++)
{
int nx=x+wx[i],ny=y+wy[i];
if(!ins(nx,ny)||!mp[nx][ny]||stp[nx][ny]f[x]+1&&ins(a,b))
{
f[cal(a,b,ob[now])]=f[x]+1;
if(!v[cal(a,b,ob[now])])
q[++t]=cal(a,b,ob[now]),v[cal(a,b,ob[now])]=1;
if(t==5001) t=0;
}
for(int l=0;l<4;l++)
if(l==now) continue;
else
{
int to=cal(i,j,l);
if(ins(i+wx[l],j+wy[l])&&mp[i+wx[l]][j+wy[l]]&&stp[i+wx[l]][j+wy[l]]f[x]+mov[i][j][now][l])
{
f[cal(i,j,l)]=f[x]+mov[i][j][now][l];
if(!v[cal(i,j,l)])
q[++t]=cal(i,j,l),v[cal(i,j,l)]=1;
if(t==5001) t=0;
}
}
}
}
}
int minn(int a,int b,int c,int d){return min(a,min(b,min(c,d)));}
void get_ans()
{
memset(f,0x3f,sizeof f);
memset(v,0,sizeof v);
bfs();
spfa();
int ans=minn(f[cal(tx,ty,0)],f[cal(tx,ty,1)],f[cal(tx,ty,2)],f[cal(tx,ty,3)]);
if(ans>=inf) ans=-1;
printf("%d\n",ans);
}
int main()
{
scanf("%d%d%d",&n,&m,&qq);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&mp[i][j]);
memset(mov,0x3f,sizeof mov);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(mp[i][j]) find(i,j);
for(int i=1;i<=qq;i++)
{
scanf("%d%d%d%d%d%d",&kx,&ky,&sx,&sy,&tx,&ty);
if(sx==tx&&sy==ty) {printf("0\n"); continue;}
get_ans();
}
return 0;
}
于是我就这样把一周的青春送给了搜索【3天】完结撒花QWQ~~~
UPD:今年愤怒的小鸟博主写了搜索45pts。。。我还是太弱了>_<
