( 题解 )第六届蓝桥杯决赛试题 -- 完美正方形 (线段树 + 深搜)
题目 :
完美正方形
如果一些边长互不相同的正方形,可以恰好拼出一个更大的正方形,则称其为完美正方形。历史上,人们花了很久才找到了若干完美正方形。比如:如下边长的22个正方形
2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60
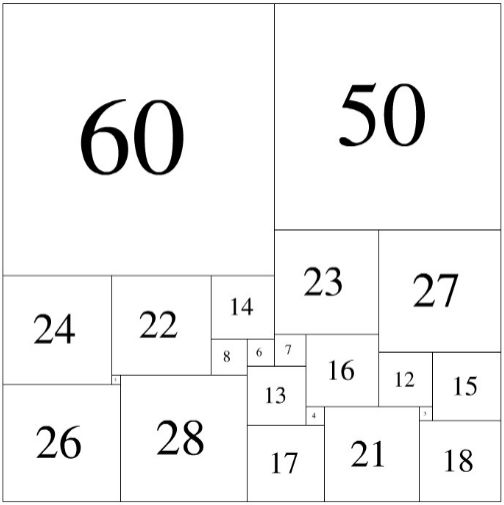
如【图1.png】那样组合,就是一种解法。此时,
紧贴上边沿的是:60 50
紧贴下边沿的是:26 28 17 21 18
22阶完美正方形一共有8种。下面的组合是另一种:
2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61
如果告诉你该方案紧贴着上边沿的是从左到右依次为:47 46 61,
你能计算出紧贴着下边沿的是哪几个正方形吗?
请提交紧贴着下边沿的正方形的边长,从左到右,用空格分开。
===================== 华丽的分割线 ===============================
当时在考场上看见这道题目的时候, 我果断选择了跳过, 首先当时就没太多思路, 其次吧, 好不容易有了思路, 觉得貌似需要线段树加深搜暴力破解, 想想肯定要耗不少时间来写代码, 对于一道填空题而言, 不太划算啊, 所有就放弃了. 直到最近, 突然回想起此题, 就花了点时间做了一下( 主要是因为在度娘上没有找到别人发的题解,所以想自己拿个沙发什么的... ).
至于思路, 我们可以效仿[俄罗斯方块]的思想, 在玩俄罗斯方块的时候, 我们总会下意识地把方块放置到高度最低的层上,同理,对于完美正方形的搭建, 由于题目已经规定了上边缘的三个块, 所以我们由上往下搭建, 而且我们知道边长为154, 由此,可以定义 :
1 .完美正方形的上边沿表示为区间[L,R]=[0,153], 区间长度为R-L+1=154 .
2 .当我们没有往里面放置任何小正方形时, 区间[0,153]的高度为0, 且整体平滑.
3 .如果区间[L, R]不平滑, 则其高度定义为-1, 表示无意义.
4 .如果区间[L, R]平滑, 则其子区间[P, Q]平滑( 其中L<=P<=Q<=R)且高度相等.
5 .如果区间[L, R]不平滑,则其父区间[P, Q]不平滑( 其中P<=L<=R<=Q).
6 .每次只能往高度最小的平滑区间内从左向右地放置小正方形M, 但M的边长不能大于区间长度.
大家看明白我的定义了吗 ? 虽然有点难理解, 但我们可以举个例子, 区间[0,153]的初始化高度为0, 整体平滑, 我们向里面放置一个边长为47的小正方形后, 区间[0,153]开始变得不平滑, 则置其高度为-1, 但其子区间[0,46]平滑且高度为47, 区间[47,153]平滑且高度依然为0. 我们继续放置一个边长为46和61的正方形后, 区间[0,153]则被分成了高度不同的三个平滑段, 其中高度最低的46.
有了上述定义, 那我们的目标就是, 每次找出高度最低的平滑区间, 尝试在上面放置正方形, 直到区间[0,153]重新平滑且高度为154时, 结果成立.
为此, 我们需要以下的一些全局变量:
#include
using namespace std;
// 全局变量
namespace Global{
const int MaxS = 46+47+61; // 正方形的边长
int All[] = {2,5,9,11,16,17,19,21,22,
24,26,30,31,33,35,36,41,50,52};// 备选正方形边长
int Length = sizeof(All)/sizeof(All[0]);// 备选正方形的数量
int Square[MaxS][MaxS]={0}; // 表示结果的完美正方形
} 接下来, 是对线段树的定义以及基本操作的方法定义.
// 线段树结点
struct TNode{
int L, R; // [L, R]
int height; // 段高度( -1时表示该段不平滑,高度无意义 )
int inc; // 高度增量
// 计算宽度
inline int Width()const{ return R-L+1;}
// 计算中点
inline int Mid()const{ return (L+R)>>1; }
}NSet[1024];
inline int LSon( int i ){ return i<<1;}
inline int RSon( int i ){ return LSon(i)+1; }
inline int Parent( int i){ return i>>1;}
// 建立线段树
void BuildTree( int i, int L, int R )
{
TNode* p = NSet+i;
p->L = L;
p->R = R;
p->height = 0;
p->inc = 0;
if( L < R ){
int m = p->Mid();
BuildTree( LSon(i), L, m );
BuildTree( RSon(i), m+1, R);
}
}// 增量的向下传递调整
// 注: NSet[i]必须为平滑区间
inline void Adjust( int i )
{
if( NSet[i].inc != 0 ){
NSet[i].height += NSet[i].inc;
if( NSet[i].L != NSet[i].R )
{
NSet[LSon(i)].inc += NSet[i].inc;
NSet[RSon(i)].inc += NSet[i].inc;
}
NSet[i].inc = 0;
}
}
// 将区间[L,R]的高度统一增加(或减少)inc
// 注: 区间 [L, R] 必须平滑
void Add(int i, int L, int R, int inc )
{
TNode* p = NSet+i;
if( p->L == L && p->R == R ){
// 操作后平滑性不变
p->inc += inc;
Adjust(i);
}
else{
int m = p->Mid();
if( p->height != -1 ) // 表示该段本是平滑的
{
Adjust(i);
p->height = -1; // 现在开始该段不再平滑
}
int ls = LSon(i), rs = RSon(i);
if( R <= m )
Add( ls, L, R, inc );
else if( L > m )
Add( rs, L, R, inc );
else{
Add( ls, L, m, inc );
Add( rs, m+1, R, inc );
}
// 平滑性恢复检验
if(NSet[ls].height != -1){
Adjust(ls);
if(NSet[rs].height != -1){
Adjust(rs);
if(NSet[ls].height == NSet[rs].height)
p->height = NSet[ls].height;
}
}
} // end else
}// 获取最低段区间
void GetLowestInterval(int i, TNode* prev, TNode* lowest )
{
TNode* p = NSet+i;
if( p->height == -1 )
{
GetLowestInterval( LSon(i), prev, lowest );
GetLowestInterval( RSon(i), prev, lowest );
}
else
{
prev->R = p->R;
// 检验等高区间连续性
if( p->height != prev->height )
{
prev->L = p->L;
prev->height = p->height;
}
// 更新最低区间
if( prev->height <= lowest->height )
{
lowest->height = prev->height;
lowest->L = prev->L;
lowest->R = prev->R;
}
}
}bool Dfs( int L, int R ,int H )
{
if( L > R )
{
TNode p, m;
m.height = 1000;
m.L = m.R = 1000;
p.height = 1000;
p.L = p.R = -1;
GetLowestInterval(1, &p, &m);
L = m.L;
R = m.R;
H = m.height;
}
int Width = R-L+1, temp=0;
if( Width == Global::MaxS && H != 0 ) return true;
for( int i = Global::Length; i-- > 0 ;)
{
temp = Global::All[i];
if( temp != 0 && temp <= Width )
{
Global::All[i] = 0;
Add( 1, L, L+temp-1, temp);
Global::Square[ H+temp-1 ][ L ] = temp;
if( Dfs( L+temp, R, H ) == true ) return true;
Add( 1, L, L+temp-1, -temp);
Global::All[i] = temp;
}
}
return false;
}int main(int argc, char** argv) {
BuildTree( 1, 0, Global::MaxS-1 );
Add( 1, 0, 46, 47);
Add( 1, 47, 92, 46);
Add( 1, 93, 153, 61);
if( Dfs( 1, 0, 0 ) ) {
for( int i = 0,t=0; i < Global::MaxS; i+=t){
t = Global::Square[ Global::MaxS-1 ][i];
cout << t << ' ';
}
}
return 0;
}