R-复数及向量下标
复数
数集拓展到实数范围内,仍有些运算无法进行。比如判别式小于0的一元二次方程仍无解,因此将数集再次扩充,达到复数范围。
形如z=a+bi的数称为复数(complex number),其中规定i为虚数单位,且i^2=i*i=-1(a,b是任意实数)
我们将复数z=a+bi中的实数a称为复数z的实部(real part)记作Rez=a
实数b称为复数z的虚部(imaginary part)记作 Imz=b.
已知:当b=0时,z=a,这时复数成为实数
当a=0且b≠0时,z=bi,我们就将其称为纯虚数。
复数的模
将复数的实部与虚部的平方和的正的平方根的值称为该复数的模,记作∣z∣.
即对于复数z=a+bi,它的模
∣z∣=√(a^2+b^2)
复数的集合用C表示,实数的集合用R表示,显然,R是C的真子集。
复数集是无序集,不能建立大小顺序
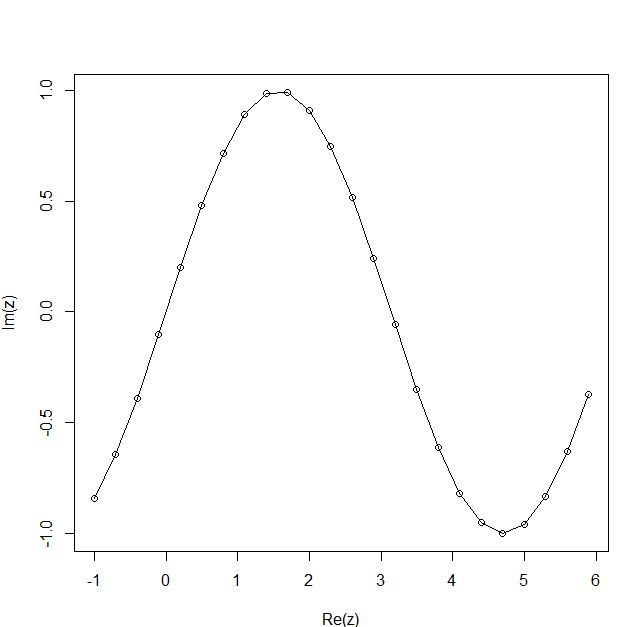
> seq(-1,6,by=.3)->x
> y=sin(x)
> z=complex(re=x,im=y)
> z
[1] -1.0-0.8414710i -0.7-0.6442177i -0.4-0.3894183i -0.1-0.0998334i
[5] 0.2+0.1986693i 0.5+0.4794255i 0.8+0.7173561i 1.1+0.8912074i
[9] 1.4+0.9854497i 1.7+0.9916648i 2.0+0.9092974i 2.3+0.7457052i
[13] 2.6+0.5155014i 2.9+0.2392493i 3.2-0.0583741i 3.5-0.3507832i
[17] 3.8-0.6118579i 4.1-0.8182771i 4.4-0.9516021i 4.7-0.9999233i
[21] 5.0-0.9589243i 5.3-0.8322674i 5.6-0.6312666i 5.9-0.3738767i
> plot(z)
> lines(z)
实部
> Re(z)
[1] -1.0 -0.7 -0.4 -0.1 0.2 0.5 0.8 1.1 1.4 1.7 2.0 2.3 2.6 2.9
[15] 3.2 3.5 3.8 4.1 4.4 4.7 5.0 5.3 5.6 5.9
虚部
> Im(z)
[1] -0.84147098 -0.64421769 -0.38941834 -0.09983342 0.19866933 0.47942554
[7] 0.71735609 0.89120736 0.98544973 0.99166481 0.90929743 0.74570521
[13] 0.51550137 0.23924933 -0.05837414 -0.35078323 -0.61185789 -0.81827711
[19] -0.95160207 -0.99992326 -0.95892427 -0.83226744 -0.63126664 -0.37387666
模
> Mod(z)
[1] 1.3069328 0.9513235 0.5582532 0.1413036 0.2819034 0.6927112 1.0745230
[8] 1.4157156 1.7120488 1.9680953 2.1970029 2.4178661 2.6506116 2.9098523
[15] 3.2005324 3.5175345 3.8489440 4.1808585 4.5017271 4.8051895 5.0911232
[22] 5.3649482 5.6354678 5.9118342
>
下标
> z[5]
[1] 0.2+0.1986693i
> z[5]<-5+6i
> z[5]
[1] 5+6i
> (z+6)[2]
[1] 5.3-0.644218i
>
> c(2,4,7,3,9,0)->x
> x[x>5]
[1] 7 9
>
> c(1:3,NA)->x
> is.na(x)
[1] FALSE FALSE FALSE TRUE
> x[!is.na(x)]->y
> y
[1] 1 2 3
>
向量的分段函数
> y[x>5]<-x[x>5]^2
> y[x<=5]<-x[x<=5]^3
> y
[1] 8 64 36 64 100
> x
[1] 2 4 6 8 10
>
> x[c(1:2,4,5)]
[1] 2 4 8 10
>
-表示扣除相应元素
> x[-c(2,4,5)]
[1] 2 6
>
字符串做为下标
> x[c(1:2,4,5)]
[1] 2 4 8 10
> x[-c(2,4,5)]
[1] 2 6
> ages<-c(x1=1,x2=2,x3=3)
> ages
x1 x2 x3
1 2 3
> c(11,22,33)->xxx
> names(xxx)<-c("x1","x2","x3")
> xxx
x1 x2 x3
11 22 33
>