krylov子空间迭代法
线性方程组: Ax = b
n次迭代后解的残差 r(n) = b - A * x(n) = ( 1- A) * x(n) + b - x(n) = x(n+1) - x(n)
n次迭代后的残差满足 b - A * x(n+1) = b - A * x(n) - A * r(n) =》 r(n+1) = r(n) - A * r(n)
故n次迭代后解形式: x(n) = x(0) + r(0) + r(1) + r(2) + .... r(n-1) = x(0) + fun(A)*r(0)
=> 原方程的解由初始解和残差的线性组合表示(即真解存在于初始解和残差项的仿射空间里)
CG 法(共轭梯度法): 求解对称正定(psd)矩阵
首先梯度方向法。根据能量极小原理: 系统误差的能量范数(2范数)取最小。梯度法即沿着系统方程曲面梯度最大的方向搜索。
更好的策略是让下一步的搜索方向与当前步的方向共轭(垂直)。
共轭: v(n) * A * v(k) = 0 ; k = 0, 1, 2,...(n-1)
解形式: x(n+1) = x(n) + v(n) * w(n) /* w(n) 是第n步搜索步长 */
=> b - A * x(n+1) + A * v(n) * w(n) = b - A *x(n) => r(n+1) = r(n) - A * v(n) * w(n)
故n次迭代后的解形式: x(n+1) = v(n) * w(n) + v(n-1) * w(n-1) + ... + v(0) * w(0) + x(0)
即“真解”存在于x(0)和n个搜索方向v(n)为正交基构成的仿射空间内。
定理一
上述“真解”误差的能量范数可分解成(n+1)个一维最小值问题(w -> x(k) + v(k) * w, k = 0, 1, ... n)
所以经过n步迭代,上述“真解”(近似解)的误差取最小能量范数。
如果 v(n)所撑起的空间 span{v0, v1, .. vn} = K_n+1(A, r0) 即梯度法的仿射空间等价Krylov子空间解。 这要求每个搜索步上的误差亦正交,亦即要求误差r(n)满足Galerkin条件
这样就是所谓的 CG 方法。 步骤如下:
A * x = b
v(0) = r(0) = b - A *x(0)
delta(0) = r(0)^2
for n = 0, ...
del(n) = v(n)^2
w(n) = delta(n)/del(n)
x(n+1) = x(n) + v(n) * w(n)
r(n+1) = r(n) - A * v(n) * w(n)
delta(n+1) = r(n+1) ^ 2
pesi(n) = delta(n+1) / delta(n)v(n+1) = r(n+1) - v(n) * pesi(n)
广义最小残差方法(GMRES): 求解非对称线性方程。Krylov子空间迭代n步之后基向量将逐渐接近而线性相关,失去正交性。为构造残差最小,需要正交化Krylov子空间的基向量 , 采用Gram–Schmidt process 正交。这样构造的Krylov子空间迭代法,有个专门的称谓:Arnoldi 迭代。 这样得到迭代n步后的残差为:
-
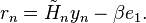
- 从该方程求解y(n), 使得 r(n) 最小。那么根据Arnoldi迭代,x(n) = Q(n) * y(n) ;
最后,非线性方程组采用(修正的)Newton方法。对于矩阵病态,初值敏感的系统,采用外层Newton迭代,内层Krylov迭代求解。此类方法称为“Newton-Krylov"方法(NKM)。NKM属于”不精确的牛顿法/inexact newton method(INM)"。
内层Krylov子空间迭代求解; J(u) * s = - F(u), 直到满足 norm( F(u) + J(u) * s )
那么外层的Newton迭代子步调整到 u(n+1) = u(n) + s
方程组的局部收敛性由系数gama控制;全局收敛性没有理论解,可由一类回溯方法(线性搜索)和一类信赖域方法近似得到。目前属于计算数学有待深入研究领域。
另外,在内层Krylov迭代中,实际上并不需要求解和存储JACOBIAN 矩阵,而是直接计算 J * s = norm ( F(u + sigma * s) - F(u) ) / sigma ,此类方法称谓” Jacobian free Newton Krylov ( JFNK)" 方法。
a brief introduction of krylov subspace method