codeforces Round #610 E - The Cake Is a Lie
codeforces Round #610 E - The Cake Is a Lie
题目:
https://codeforces.com/contest/1282/problem/E
We are committed to the well being of all participants. Therefore, instead of the problem, we suggest you enjoy a piece of cake.
Uh oh. Somebody cut the cake. We told them to wait for you, but they did it anyway. There is still some left, though, if you hurry back. Of course, before you taste the cake, you thought about how the cake was cut.
It is known that the cake was originally a regular nn-sided polygon, each vertex of which had a unique number from 11 to nn. The vertices were numbered in random order.
Each piece of the cake is a triangle. The cake was cut into n−2n−2 pieces as follows: each time one cut was made with a knife (from one vertex to another) such that exactly one triangular piece was separated from the current cake, and the rest continued to be a convex polygon. In other words, each time three consecutive vertices of the polygon were selected and the corresponding triangle was cut off.
A possible process of cutting the cake is presented in the picture below.
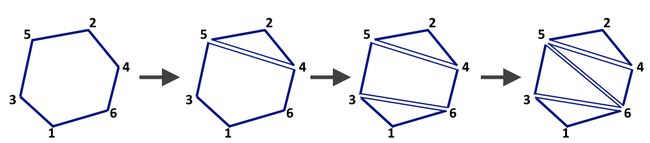 Example of 6-sided cake slicing.
Example of 6-sided cake slicing.
You are given a set of n−2n−2 triangular pieces in random order. The vertices of each piece are given in random order — clockwise or counterclockwise. Each piece is defined by three numbers — the numbers of the corresponding nn-sided cake vertices.
For example, for the situation in the picture above, you could be given a set of pieces: [3,6,5],[5,2,4],[5,4,6],[6,3,1][3,6,5],[5,2,4],[5,4,6],[6,3,1].
You are interested in two questions.
- What was the enumeration of the nn-sided cake vertices?
- In what order were the pieces cut?
Formally, you have to find two permutations p1,p2,…,pnp1,p2,…,pn (1≤pi≤n1≤pi≤n) and q1,q2,…,qn−2q1,q2,…,qn−2 (1≤qi≤n−21≤qi≤n−2) such that if the cake vertices are numbered with the numbers p1,p2,…,pnp1,p2,…,pn in order clockwise or counterclockwise, then when cutting pieces of the cake in the order q1,q2,…,qn−2q1,q2,…,qn−2 always cuts off a triangular piece so that the remaining part forms one convex polygon.
For example, in the picture above the answer permutations could be: p=[2,4,6,1,3,5]p=[2,4,6,1,3,5] (or any of its cyclic shifts, or its reversal and after that any cyclic shift) and q=[2,4,1,3]q=[2,4,1,3].
Write a program that, based on the given triangular pieces, finds any suitable permutations pp and qq.
Input
The first line contains a single integer tt (1≤t≤10001≤t≤1000) — the number of test cases. Then there are tt independent sets of input data.
The first line of each set consists of a single integer nn (3≤n≤1053≤n≤105) — the number of vertices in the cake.
The following n−2n−2 lines describe the numbers of the pieces vertices: each line consists of three different integers a,b,ca,b,c (1≤a,b,c≤n1≤a,b,c≤n) — the numbers of the pieces vertices of cake given in random order. The pieces are given in random order.
It is guaranteed that the answer to each of the tests exists. It is also guaranteed that the sum of nn for all test cases does not exceed 105105.
Output
Print 2t2t lines — answers to given tt test cases in the order in which they are written in the input. Each answer should consist of 22 lines.
In the first line of an answer on a test case print nn distinct numbers p1,p2,…,pnp1,p2,…,pn(1≤pi≤n1≤pi≤n) — the numbers of the cake vertices in clockwise or counterclockwise order.
In the second line of an answer on a test case print n−2n−2 distinct numbers q1,q2,…,qn−2q1,q2,…,qn−2(1≤qi≤n−21≤qi≤n−2) — the order of cutting pieces of the cake. The number of a piece of the cake corresponds to its number in the input.
If there are several answers, print any. It is guaranteed that the answer to each of the tests exists.
Example:
input:
3
6
3 6 5
5 2 4
5 4 6
6 3 1
6
2 5 6
2 5 1
4 1 2
1 3 5
3
1 2 3
output:
1 6 4 2 5 3
4 2 3 1
1 4 2 6 5 3
3 4 2 1
1 3 2
1
题意:
把一个 n 边形割成 n−2 个三角形,给出这 n−2 个三角形三个顶点标号,构造出 p、q 数组,p 数组表示这个 n 边形顺时针或者逆时针走一圈各个点的标号,q数组表示切割三角形的顺序。
思路:
有两问:第一、确定这个 n 边形的标号。考虑 n 边形的 n 条边一定是在且只在一个三角形内,而通过切割后出现的边,则一定会使用两次。
那么只要把三角形的边存起来,然后看对于每一个顶点 u,若存在一个从 u 到 v 的边,则说明 u−v 这条边在一个三角形内出现过,那么只要找到每个 u 和其相连的且只出现一次的 v,把 v 放在 u 两侧即可,然后通过 dfs 一个一个搜出来就可以了。
第二问简单,想要切下来一个三角形,那么这个三角形一定是两个边在最外侧,一个边还没切割出来,然后去切割这还没被切割出来的边,那么通过拓扑排序来一个个切就可以了。
#include