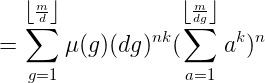2019-2020 ICPC Asia Yinchuan Regional Contest【银川现场赛】
题目:
2019-2020 ICPC Asia Yinchuan Regional onsite
A. Girls Band Party
题意:
咕咕咕
分析:
题目要求选出 5 张名字不一样的牌,那就先将卡牌按名字分类,每一类最多只能选一个;定义 dp[i][j][k] 表示前 i 类加成为 j,且已经选了 k 张牌时的最大 power 和;j 最大为 150,但每次只会加 10 和 20,开到 15 即可
代码:
#include
#define x first
#define y second
#define pii pair
#define sz(x) (int)(x).size()
#define Max(x,y) (x)>(y)?(x):(y)
#define Min(x,y) (x)<(y)?(x):(y)
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long LL;
const LL inf = -1e18;
const int maxn = 1e5+15;
struct node{
char Name[15],Color[15];
int power;
}A;
char color[15];
LL dp[maxn][16][6];
vector v[maxn];
unordered_map mp,np;
int main(){
int T,n,cnt = 0;
for(int i = 0;i < 16; ++i)
for(int j = 0;j < 6; ++j)
dp[0][i][j] = inf;
dp[0][0][0] = 0; scanf("%d",&T);
while(T--){
scanf("%d",&n); mp.clear(), np.clear();
for(int i = 1;i <= cnt; ++i) v[i].clear();
cnt = 0;
for(int i = 1;i <= n; ++i){
scanf("%s %s %d",A.Name,A.Color,&A.power);
if(np.count(A.Name)) v[np[A.Name]].push_back(A);
else np[A.Name] = ++cnt, v[cnt].push_back(A);
}
for(int i = 1;i <= 5; ++i) scanf("%s",color),mp[color] = 1;
scanf("%s",color);
for(int i = 1;i <= cnt; ++i){
for(int j = 0;j < 16; ++j)
for(int k = 0;k < 6; ++k)
dp[i][j][k] = dp[i-1][j][k];
for(int s = 0;s < sz(v[i]); ++s){
int w = 0;
if(mp.count(v[i][s].Name)) w++;
if(strcmp(v[i][s].Color,color)==0) w+=2;
for(int j = w;j < 16; ++j)
for(int k = 1;k < 6; ++k)
dp[i][j][k] = Max(dp[i][j][k],dp[i-1][j-w][k-1]+v[i][s].power);
}
}
LL ans = 0;
for(int i = 0;i < 16; ++i){
if(dp[cnt][i][5] > 0) ans = Max(ans,dp[cnt][i][5]*(10+i)/10);
}
cout << ans << '\n';
}
return 0;
}
D. Easy Problem
题意:
分析:
题目相当于求解:
由于 n 很大,套用广义欧拉降幂就做完了
代码:
#include
#define x first
#define y second
#define pii pair
#define sz(x) (int)(x).size()
#define Max(x,y) (x)>(y)?(x):(y)
#define Min(x,y) (x)<(y)?(x):(y)
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long LL;
const int maxn = 1e5+15;
const int mod = 59964251;
int prime[maxn],mul[maxn],vis[maxn];
LL qpow(LL a,LL x,LL mod){
LL res = 1ll;
while(x){
if(x&1) res = res * a % mod;
a = a * a % mod;
x >>= 1;
}
return res;
}
LL sum[maxn],d,k,m;
char s[maxn];
void init(){
mul[1] = 1; int tot = 0;
for(int i = 2;i < maxn; ++i){
if(!vis[i]){
prime[tot++] = i; mul[i] = -1;
}
for(int j = 0;j= mod) sum[i] -= mod;
}
for(int i = 1;i <= m; ++i){
ans += mul[i]*qpow(i*d,x*k,mod)*qpow(sum[m/i],x,mod)%mod+mod;
ans %= mod;
}
return int(ans);
}
int Eular(int x){
int phi = x;
for(int i = 2;1ll*i*i<=x; ++i){
if(x%i == 0){
phi = phi/i*(i-1);
while(x%i == 0) x /= i;
}
}
if(x > 1) phi = phi/x*(x-1);
return phi;
}
int main(){
int T; scanf("%d",&T); init();
int phi = Eular(mod);
while(T--){
scanf("%s %lld %lld %lld",s,&m,&d,&k);
int len = strlen(s); bool flag = false;
LL x = 0;
for(int i = 0;i < len; ++i){
x = x*10+(s[i]-'0');
if(x >= phi) x %= phi,flag = true;
}
if(flag) x += phi;
printf("%d\n",solve(x));
}
return 0;
} F. Function!
题意:
分析:
根据反函数的定义,题目相当于求解:
时,后面 log 函数恒等于 1,前面 log 函数的值可以分成 [a,a^2),[a^2,a^3)... [a^k,n] 分成 log 段计算,当 a > sqrt(n) 时,前面的 log 函数又恒等于 1 ,化简公式后可以直接 O(1) 计算
代码:
#include
#define x first
#define y second
#define pii pair
#define sz(x) (int)(x).size()
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long LL;
const int maxn = 1e5+15;
const int mod = 998244353;
const int inv2 = 499122177;
const int inv6 = 166374059;
LL qpow(LL a,LL x,LL mod){
LL res = 1ll;
while(x){
if(x&1) res = res*a%mod;
a = a*a%mod;
x >>= 1;
}
return res;
}
LL per(LL x){
x %= mod;
return x*(x+1)%mod*(2*x+1)%mod*inv6%mod;
}
LL cal(LL l,LL r,LL n){
LL ans = (r-l+1)%mod*((r+l)%mod)%mod*((n+1)%mod)%mod*inv2%mod-per(r)+mod+per(l-1);
return ans%mod;
}
inline int sqr(LL n){
LL x = sqrt(n*1.0);
for(int i = x+2;i >= x-2; --i){
if(1ll*i*i <= n) return i;
}
}
LL solve(LL n){
int k = sqr(n);
LL ans = 0;
for(int a = 2;a <= k; ++a){
LL s = a,cnt = 1;
while(s*a <= n){
ans += (s*a-s)%mod*a%mod*cnt%mod;
if(ans >= mod) ans -= mod;
cnt++; s = s*a;
}
ans += (n-s+1)%mod*cnt%mod*a%mod;
if(ans >= mod) ans -= mod;
}
ans += cal(k+1,n,n);
return ans%mod;
}
int main(){
LL n; cin >> n;
cout << solve(n) << '\n';
return 0;
} G. Pot!!
题意:
分析:
查询等价于求区间内的每个数唯一分解后,指数的最大值,注意到
,直接对 2,3,5,7 每个质因子开一颗线段树维护幂的最值,更新操作就相当于区间加
代码:
#include
#define x first
#define y second
#define pii pair
#define sz(x) (int)(x).size()
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long LL;
const int maxn = 1e5+15;
int prime[4] = {2,3,5,7};
int tr[4][maxn<<2],lz[4][maxn<<2],n,q,l,r,x;
char op[100];
inline void pushdown(int o,int x){
tr[o][x<<1] += lz[o][x]; tr[o][x<<1|1] += lz[o][x];
lz[o][x<<1] += lz[o][x]; lz[o][x<<1|1] += lz[o][x];
lz[o][x] = 0;
}
void updata(int l,int r,int L,int R,int x,int o,int v){
if(l > R || r < L) return ;
if(l >= L && r <= R){
tr[o][x] += v;
lz[o][x] += v;
return ;
}
if(lz[o][x]) pushdown(o,x);
int mid = (l+r) >> 1;
updata(l,mid,L,R,x<<1,o,v);
updata(mid+1,r,L,R,x<<1|1,o,v);
tr[o][x] = max(tr[o][x<<1],tr[o][x<<1|1]);
}
void query(int l,int r,int L,int R,int x,int &ans){
if(l > R || r < L) return ;
if(l >= L && r <= R){
for(int i = 0;i < 4; ++i) ans = max(tr[i][x],ans);
return ;
}
for(int i = 0;i < 4; ++i){
if(lz[i][x]) pushdown(i,x);
}
int mid = (l+r) >> 1;
query(l,mid,L,R,x<<1,ans);
query(mid+1,r,L,R,x<<1|1,ans);
}
int main(){
cin >> n >> q;
for(int i = 1;i <= q; ++i){
scanf("%s",op);
if(op[1] == 'U'){
scanf("%d %d %d",&l,&r,&x);
for(int i = 0;i < 4; ++i){
if(x%prime[i] == 0){
int cnt = 0;
while(x%prime[i] == 0){
cnt++; x /= prime[i];
}
updata(1,n,l,r,1,i,cnt);
}
}
}
else{
scanf("%d %d",&l,&r);
int ans = 0;
query(1,n,l,r,1,ans);
printf("ANSWER %d\n",ans);
}
}
return 0;
} I. Base62
题意:
分析:
Python ![]() 大力模拟即可,注意特判
大力模拟即可,注意特判 ![]()
代码:
a = input().split();
x = int(a[0]); y = int(a[1])
z = list(a[2]); z.reverse();
sum = 0; b = 1;
for i in z:
if i.isdigit():
sum += int(i)*b
elif i.islower():
sum += ((ord(i)-ord('a'))+36)*b
elif i.isupper():
sum += ((ord(i)-ord('A'))+10)*b
b *= x
if sum == 0:
print(0)
else:
ans = []
while sum > 0:
ans.append(sum%y)
sum = sum//y
ans.reverse()
for i in ans:
if i < 10:
print(i,end='')
elif i < 36:
print(chr(ord('A')+i-10),end='')
else:
print(chr(ord('a')+i-36),end='')H. Delivery Route
题意:
分析:
有负权边,不能直接跑 dij,跑 SPFA 复杂度说不过去(玄学优化也能过),题解的做法是先将双向边缩环,然后建立拓扑图,在走拓扑的过程中用拓扑图的边去更新最短路,然后对强连通分量内部跑 dij,
原题:Loj - 10081
代码:
#include
#define x first
#define y second
#define pii pair
#define sz(x) (int)(x).size()
#define Max(x,y) (x)>(y)?(x):(y)
#define Min(x,y) (x)<(y)?(x):(y)
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long LL;
const LL inf = 1e18;
const int maxn = 1e5+15;
int tot1,tot2,head[maxn],Head[maxn];
struct edge{
int to,nxt,w;
}e[maxn<<1],E[maxn<<1];
inline void adde(int u,int v,int w){
e[++tot1] = (edge){v,head[u],w};
head[u] = tot1;
}
inline void addE(int u,int v,int w){
E[++tot2] = (edge){v,Head[u],w};
Head[u] = tot2;
}
int dfn[maxn],low[maxn],instack[maxn],id[maxn],num,cnt;
vector vv[maxn];
stack ss;
void Tarjan(int x){
dfn[x] = low[x] = ++num; ss.push(x),instack[x] = 1;
for(int i = head[x];i > 0;i = e[i].nxt){
int v = e[i].to;
if(!dfn[v]){
Tarjan(v);
low[x] = min(low[x],low[v]);
}
else if(instack[v]) low[x] = min(low[x],dfn[v]);
}
if(low[x] == dfn[x]){
++cnt; int v;
do{
v = ss.top(); ss.pop();
id[v] = cnt; instack[v] = 0;
vv[cnt].push_back(v);
}while(v != x);
}
}
struct node{
int x; LL w;
friend bool operator<(node a,node b){
return a.w > b.w;
}
};
LL dis[maxn];
void dijkstra(int s){
priority_queue q;
for(int i = 0;i < sz(vv[s]); ++i)
q.push((node){vv[s][i],dis[vv[s][i]]});
while(!q.empty()){
node now = q.top(); q.pop();
if(now.w < dis[now.x]) continue;
for(int i = head[now.x];i > 0;i = e[i].nxt){
int v = e[i].to; if(id[v] != s) continue;
if(dis[v] > dis[now.x]+e[i].w){
dis[v] = dis[now.x] + e[i].w;
q.push((node){v,dis[v]});
}
}
}
}
int vis[maxn],in[maxn];
pii p[maxn];
void dfs(int x,int fa){ //从新建拓扑图
vis[x] = 1;
for(int i = head[x];i > 0;i = e[i].nxt){
int v = e[i].to; if(v == fa) continue;
if(id[x] != id[v]){
addE(id[x],id[v],e[i].w);
p[tot2] = pii(x,v); in[id[v]]++;
}
if(!vis[v]) dfs(v,x);
}
}
void Topology(int s){
queue q;
for(int i = 1;i <= cnt; ++i){
if(in[i] == 0) q.push(i),dijkstra(i);
}
while(!q.empty()){
int x = q.front(); q.pop();
for(int i = Head[x];i > 0;i = E[i].nxt){
int v = E[i].to;
dis[p[i].y] = min(dis[p[i].y],dis[p[i].x]+E[i].w); //拓扑边更新最短路
if(--in[v] == 0) q.push(v),dijkstra(v);
}
}
}
int main(){
int n,x,y,s,a,b,c;
scanf("%d %d %d %d",&n,&x,&y,&s);
while(x--){
scanf("%d %d %d",&a,&b,&c);
adde(a,b,c); adde(b,a,c);
}
while(y--){
scanf("%d %d %d",&a,&b,&c);
adde(a,b,c);
}
for(int i = 1;i <= n; ++i) dis[i] = inf;
dis[s] = 0; Tarjan(s); dfs(s,0); Topology(s);
for(int i = 1;i <= n; ++i){
if(dis[i] >= 1000000000) puts("NO PATH");
else printf("%d\n",(int)dis[i]);
}
return 0;
} K. Largest Common Submatrix
题意:
分析:
通过 BFS 将映射的连通块标记出来,然后就相当于在一个填满数字的矩阵中找一个数字都一样的最大子矩阵,可以用单调栈,也可以悬线法dp,这题时间有点吃紧,需要快读
代码:
#include
#define x first
#define y second
#define pii pair
#define sz(x) (int)(x).size()
#define Max(x,y) (x)>(y)?(x):(y)
#define Min(x,y) (x)<(y)?(x):(y)
#define all(x) (x).begin(),(x).end()
using namespace std;
typedef long long LL;
const int maxn = 1e3+13;
const int maxm = 1e6+16;
const int mod = 1e9+7;
int n,m,cnt,a[maxn][maxn],b[maxn][maxn],px[maxm],py[maxm];
int up[maxn][maxn],L[maxn][maxn],R[maxn][maxn],vis[maxn][maxn];
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
struct node{
int ax,ay,bx,by;
};
inline bool check(int x,int y){
return x > 0 && x <= n && y > 0 && y <= m;
}
inline int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)) {if(c == '-') f=-1; c=getchar();}
while(isdigit(c)) {x = x*10+c-'0'; c = getchar();}
return x * f;
}
inline void write(int x) {
if (x >= 10) write(x / 10);
putchar(x % 10 + '0');
}
void bfs(int x,int y){
queue q;
q.push((node){x,y,px[a[x][y]],py[a[x][y]]});
a[x][y] = ++cnt; vis[x][y] = 1;
while(!q.empty()){
node now = q.front(); q.pop();
for(int i = 0;i < 4; ++i){
int fax = now.ax+dx[i],fay = now.ay+dy[i];
int fbx = now.bx+dx[i],fby = now.by+dy[i];
if(check(fax,fay)&&check(fbx,fby)&&!vis[fax][fay]&&a[fax][fay]==b[fbx][fby]){
vis[fax][fay] = 1; a[fax][fay] = cnt;
q.push((node){fax,fay,fbx,fby});
}
}
}
}
int solve(){
int ans = 0;
for(int i = 1;i <= n; ++i){
for(int j = m;j > 0; --j){
if(a[i][j] != a[i][j+1]) R[i][j] = j;
else R[i][j] = R[i][j+1];
}
for(int j = 1;j <= m; ++j){
if(a[i][j] != a[i][j-1]) L[i][j] = j;
else L[i][j] = L[i][j-1];
}
for(int j = 1;j <= m; ++j){
if(a[i-1][j] == a[i][j]){
up[i][j] = up[i-1][j]+1;
L[i][j] = Max(L[i-1][j],L[i][j]);
R[i][j] = Min(R[i-1][j],R[i][j]);
}
else up[i][j] = 1;
ans = Max(ans,up[i][j]*(R[i][j]-L[i][j]+1));
}
}
return ans;
}
int main(){
n = read(),m = read();
for(int i = 1;i <= n; ++i)
for(int j = 1;j <= m; ++j)
a[i][j] = read();
for(int i = 1;i <= n; ++i){
for(int j = 1;j <= m; ++j){
b[i][j] = read();
px[b[i][j]] = i; py[b[i][j]] = j;
}
}
for(int i = 1;i <= n; ++i){
for(int j = 1;j <= m; ++j){
if(!vis[i][j]) bfs(i,j);
}
}
write(solve());
return 0;
} 再贴个单调栈的 solve():
int solve(){
int ans = 0;
for(int i = 1;i <= n; ++i){
stack s; int left = 1,right = m;
for(int j = 1;j <= m; ++j){
if(a[i][j] == a[i-1][j]) c[j] += 1;
else c[j] = 1;
if(a[i][j] != a[i][j-1]){
while(!s.empty()) s.pop();
left = j;
}
while(!s.empty()&&c[s.top()]>=c[j]) s.pop();
if(!s.empty()) dp[j] = s.top()+1;
else dp[j] = left;
s.push(j);
}
while(!s.empty()) s.pop();
for(int j = m;j > 0; --j){
if(a[i][j] != a[i][j+1]){
while(!s.empty()) s.pop();
right = j;
}
while(!s.empty()&&c[s.top()]>=c[j]) s.pop();
if(!s.empty()) ans = Max(ans,c[j]*(s.top()-dp[j]));
else ans = Max(ans,c[j]*(right-dp[j]+1));
s.push(j);
}
}
return ans;
}
![\large \sum_{a_1=1}^{m}\sum_{a_2=1}^{m}...\sum_{a_n=1}^{m}\left ( a_1a_2...a_n \right )^k[gcd(a_1,a_2,...,a_n)==d]](http://img.e-com-net.com/image/info8/9dd1e02903e44cfbb824e97fdc62a64d.gif)