随机信号处理之功率谱估计中均方误差随信噪比变化的情况
本博客是在之前一篇博客Levinson-Durbin递推算法的基础上,另外编写了一个程序,以N=256点,P=128阶为例,分析频率估计的均方误差和信噪比之间的关系。由未加噪声的信号使用自相关法求出信号功率Power,分别取噪声功率为1-10000即(标准差a为1-100),转化为信噪比关系:
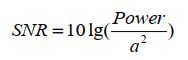
每种噪声标准差情况下进行500次求功率谱并寻峰进行频率估计,求出对应的频率估计的均方误差并画出与SNR的关系曲线:
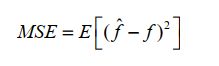
MATLAB程序结果:
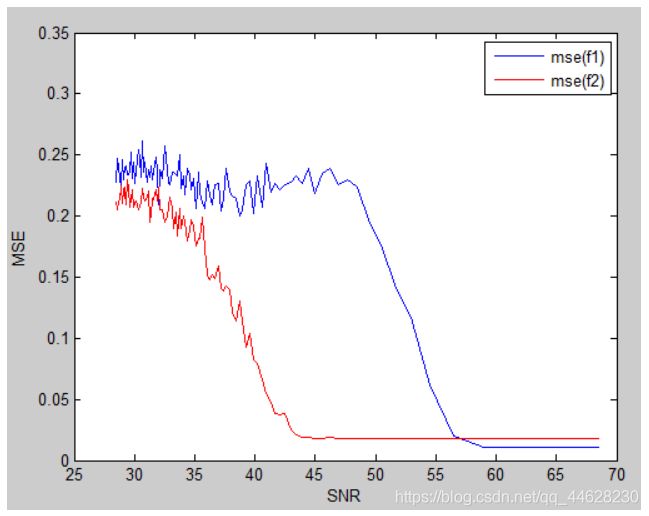
Python程序结果:
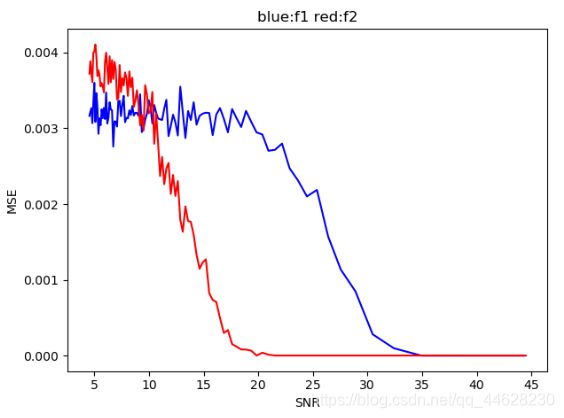
实验结果与理论情况相符合,MSE 都有一个随着 SNR 增大而减小的过程,f1相对于f2 ,受到噪声影响较大,随着SNR 的减小,其MSE升高的更早。
MATLAB程序:
clc
clear
%构造加入高斯白噪声的原函数
f1=0.1;f2=0.13;
N=256;
p=128;
n=1:N;
xn=2*sin(2*pi*f1*n+pi/3)+10*sin(2*pi*f2*n+pi/4);
%求未加噪声的信号的自相关函数
Rx=xcorr(xn);
%求自相关的DFT,即功率谱密度,然后求得信号功率
Sx=abs(fft(Rx,N));
Power=sum(Sx);
msef1=zeros(1,100);
msef2=zeros(1,100);
SNR=zeros(1,100);
for sigma=1:100
wucha1=0;
wucha2=0;
count=500;
for cishu=1:count
wn=sigma*randn(1,N);
yn=xn+wn;
%求自相关函数,取实际的Rx(0)-Rx(p)部分
Rm=xcorr(yn,'biased');
R=zeros(1,p+1);
for i=1:p+1 %其中索引从1开始,故用R(1)--R(p+1)代表Rx(0)--Rx(p)
R(i)=Rm(N+i-1);
end
%LevinsonDurbin递推
a=zeros(p);
k=zeros(1,p);
rou=zeros(1,p);
a(1,1)=-R(2)/R(1);
k(1)=a(1,1);
rou(1)=R(1)*(1-k(1)^2);%1阶初始条件,实际初始条件是0阶,但是为了避免索引为0,从1阶开始使用
for m=2:p
a(m,m)=-R(m+1)/rou(m-1);%用作初始条件,下面加上累加项
for i=1:m-1
a(m,m)=a(m,m)-(a(m-1,i)*R(m+1-i))/rou(m-1);
end
k(m)=a(m,m);
if k(m)>1
break;
end
for j=1:m-1
a(m,j)=a(m-1,j)+k(m)*a(m-1,m-j);
end
rou(m)=rou(m-1)*(1-(k(m))^2);
end
%得到p+1个参数,求频率响应
G2=rou(p);
ap=zeros(1,p);
for k=1:p
ap(k)=a(p,k);
end
[H,w] = freqz(G2^0.5,[1,ap],N);
Hf = abs(H);
Sx=Hf.^2;
%估计f1,f2
[pks,locs] = findpeaks(Sx,'SortStr','descend');%寻峰并降序排列
f1_guji=locs(2)/N;
f2_guji=locs(1)/N;
wucha1=wucha1+(f1_guji-f1).^2;
wucha2=wucha2+(f2_guji-f2).^2; %500次的误差平方累加
end
msef1(sigma)=wucha1/count;
msef2(sigma)=wucha2/count;
SNR(sigma)=10*log10(Power/(sigma*sigma));
end
plot(SNR,msef1,'-b');
hold on
plot(SNR,msef2,'-r');
xlabel('SNR');
ylabel('MSE');
legend('mse(f1)', 'mse(f2)');
Python程序:
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal
import math
#自定义自相关函数
def xcorr(data):
length=len(data)
R=[]
for m in range(0,length):
sum = 0.0
for n in range(0,length-m):
sum=sum+data[n]*data[n+m]
R.append(sum/length)
return R
N=256
p=128
#构造原函数
f1=0.1
f2=0.13
n=np.linspace(0,N-1,N)
xn=2*np.sin(2*np.pi*f1*n+np.pi/3)+10*np.sin(2*np.pi*f2*n+np.pi/4)
#求自相关
Rx=xcorr(xn)
#求信号功率
Sx=abs(np.fft.fft(Rx))
Power=sum(Sx)
#加入高斯白噪声
msef1=[]
msef2=[]
SNR=[]
for sigma in range(1,100):
wucha1=0.0
wucha2=0.0
count=500
for cishu in range(1,count):
wn=np.random.normal(0,sigma,len(xn))
yn=[]
for x,y in zip(xn,wn):
z=x+y
yn.append(z)
#求自相关
R=xcorr(yn)
#递推初始条件
a=np.zeros([p+1,p+1])
rou=np.zeros(p+1)
k=np.zeros(p+1)
rou[0]=R[0]
k[0]=1
a[1][1]=-R[1]/rou[0]
k[1]=a[1][1]
rou[1]=rou[0]*(1-(k[1]**2))
#递推
for m in range(2,p+1):
a[m][m]=-R[m]/rou[m-1]
for i in range(1,m):
a[m][m]=a[m][m]-(a[m-1][i]*R[m-i])/rou[m-1]
k[m]=a[m][m]
if k[m]>1:
break
for i in range(1,m):
a[m][i]=a[m-1][i]+k[m]*a[m-1][m-i]
rou[m]=rou[m-1]*(1-(k[m]**2))
#得到p+1个参数,求频率响应
G2=rou[p]
ap=[]
for k in range(1,p+1):
ap.append(a[p][k])
apk=np.insert(ap,0,[1])
G=np.sqrt(G2)
#计算频率响应
w,h=scipy.signal.freqz(G,apk,worN=N)
Hf=abs(h)
Sx=Hf**2
#估计f1,f2
s=int(0.115*2*N)
f1_guji=(np.argmax(Sx[0:s]))/(2*N)
f2_guji=(np.argmax(Sx[s:int(N/2)])+s)/(2*N)
wucha1=wucha1+(f1_guji-f1)**2
wucha2=wucha2+(f2_guji-f2)**2
msef1.append(wucha1/count)
msef2.append(wucha2/count)
snr=10*math.log(Power/(sigma*sigma),10)
SNR.append(snr)
plt.plot(SNR,msef1,"-b")
plt.plot(SNR,msef2,"-r")
plt.xlabel("SNR")
plt.ylabel("MSE")
plt.title("blue:f1 red:f2")
plt.show()
其他几种算法也都有进行MSE随SNR曲线的求解和绘制,与此相类似,故不再赘述,可以查看以下资源:
现代法功率谱估计以及MSE随SNR曲线