如何进行特征选择(代码篇)| 机器学习你会遇到的“坑”
转载自:https://baijiahao.baidu.com/s?id=1604162212692449062&wfr=spider&for=pc
仅做记录,侵删。
我们在这里首先会对数据的多余特征和无关特征做可视化,以便我们更好的理解特征选择的动机,接着分别用过滤法,包裹法,和嵌入法这些特征选择的方法做出代码展示,同时观察测试集上泛化误差来体现出特征选择的优越性,最后我们试一试将其结合起来会不会取得更好的效果。
我们上一篇的所用的糖尿病数据有一个遗留问题,那就是性别到底与糖尿病的恶化程度有没有关系?换而言之,它到底是不是一个无关特征?
from sklearn import datasets
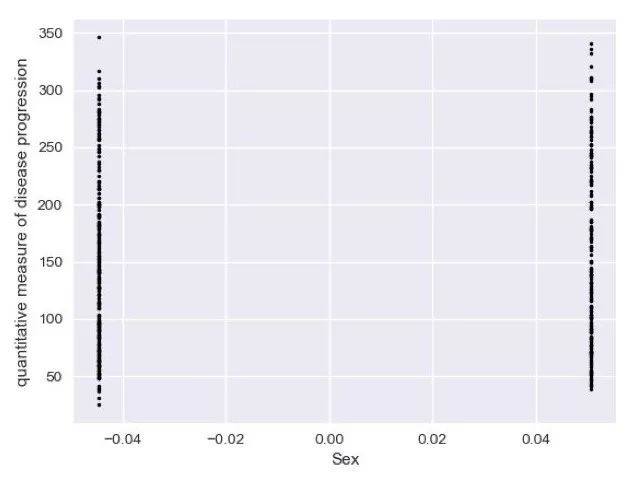
import seaborn as snsimport matplotlib.pyplot as pltimport numpy as np#读取数据data=datasets.load_diabetes()X=data['data'][:,np.newaxis,1]y=data['target']#作图sns.set(style='darkgrid')plt.plot(X,y,'.k',markersize=5)plt.xlabel('Sex')plt.ylabel('quantitativemeasure of disease progression')plt.legend()plt.show()
我们从图中可以看出来,在每个性别上,我们的目标均呈现出均匀分布的趋势,很可能性别就是一个无关特征,但是,我们最好利用相关系数法来对所有的特征做一个检验:
from sklearn import datasets
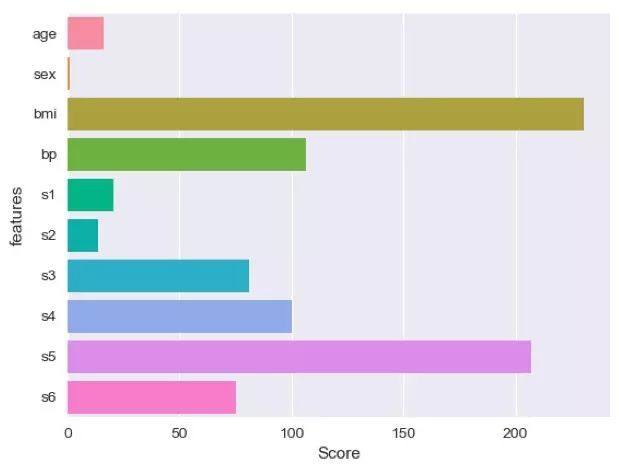
fromsklearn.feature_selection import f_regressionimport seaborn as snsimport matplotlib.pyplot as pltimport numpy as np#读取数据data=datasets.load_diabetes()X=data['data']y=data['target']# 计算相关系数score=f_regression(X,y)[0]#作图sns.set(style='darkgrid')sns.barplot(score,data['feature_names'])plt.xlabel('Score')plt.ylabel('features')plt.legend()plt.show()
相关系数衡量的是特征与目标的线性相关性,从图中可以看出,性别与目标的相关系数非常小,那么其余的诸如‘age’,'s1','s2'该不该去除呢,我们在对特征做互信息筛选:
......
fromsklearn.feature_selection import mutual_info_regressionscore=mutual_info_regression(X,y,discrete_features=False,random_state=0)......
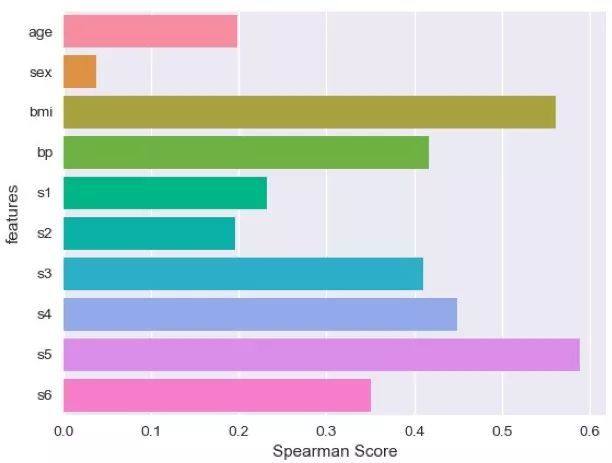
除此之外,我们还可以选用Spearman相关系数:
from scipy.stats import spearmanr
score=[]forn in range(10): score.append(np.abs(spearmanr(X[:,n],y)[0]))
可以看出,‘age’,‘sex’,‘s1’,‘s2’仍然是得分最低的四个特征,而‘age’,‘sex’,‘s2’仍然是得分最低的三个特征。我们就可以说,互信息和Pearson系数,以及Spearman系数取得了一定程度的一致性。那么经过这样的过滤,我们对特征的重要程度有了认识,到底要挑选多少特征进入最终的模型取决于多少特征可以达到最好的性能。
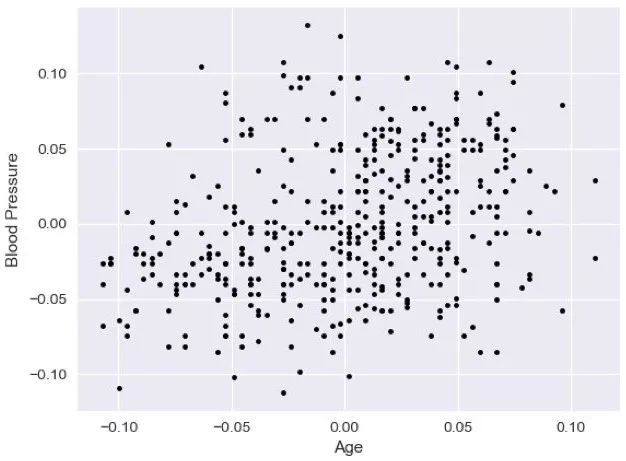
直到这里,我们做的只是检验特征与目标的相关性,来达到剔除无关特征的作用,但是除此之外,我们的特征选择还有一个重要的任务,就是剔除多余特征。针对我们的数据,我们可能会直觉上认为,年龄和血压有一定的关系:
plt.plot(X[:,0],X[:,3],'.k')
但如果我们只从样本空间去可视化,我们无法做到精确判断,比如这幅图我们无法得到什么信息。更好的做法是,我们对每个特征与每个特征做相关系数,得到相关性矩阵(注意,这时候我们只对特征进行处理,与目标i无关):
from scipy.stats import spearmanr
import seaborn as snsfrom sklearn import datasets
data=datasets.load_diabetes()X=data['data']
score_mat=np.abs(spearmanr(X)[0])
sns.set(style='white')
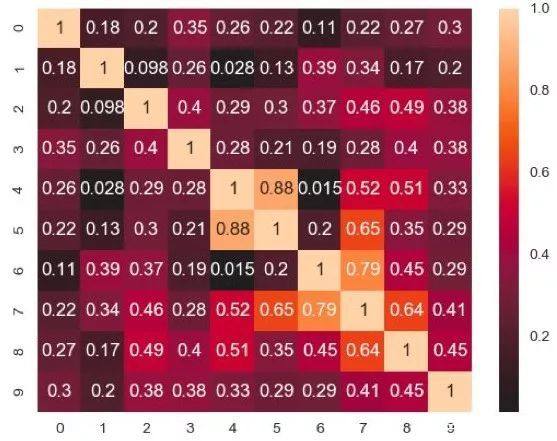
sns.heatmap(score_mat,annot=True,center=0)plt.show()
方格的颜色越浅,相关程度越高。我们可以注意到一个有趣的事实:我们所关注的年龄和血压的相关度只有0.35,远远低于's1'血清与's2'血清的相关度,后者高达0.88,而's3'血清和's4'血清的相关度也有0.79.为了直观的理解这种相关度,我们可以对高相关度的's1'血清和's2'血清做图:
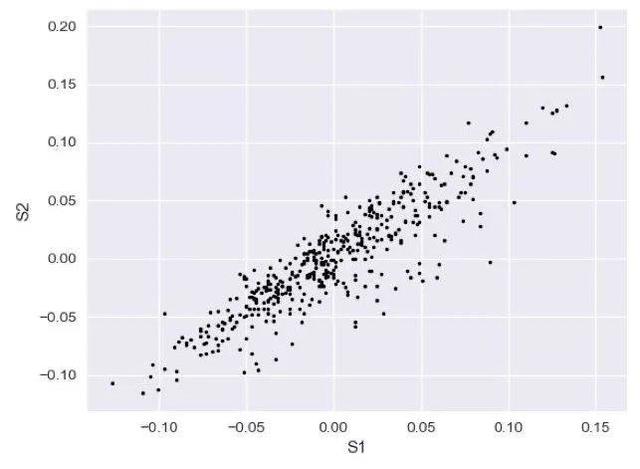
plt.plot(X[:,4],X[:,5],'.k')
两者呈现出很强的线性关系!那么我们就可以断定这是多余特征的特征,我们只需要保留其中一个。
由上可见,过滤法主要有两大任务:通过检验特征之间的相关度来找出多余特征,通过检验特征与目标的相关度来找出无关特征。
接下来,包裹法相对就好理解得多,它把全部的特征丢进集合,利用贪心策略。我们可以只利用线性模型观察不同的特征数对模型拟合能力的影响,根据理论我们说特征越少,模型的参数也就越少,那么模型的拟合能力也会越弱。但是,特征选择的目的是为了让模型的泛化能力更强,所以我们要把特征数当作超参数,通过交叉验证的办法来观察测试集的上的泛化误差:
from sklearn.feature_selection import RFECV
import seaborn as snsimport matplotlib.pyplot as pltimport numpy as npfrom sklearn.linear_model import LinearRegressionfromsklearn.model_selection import KFolddata=datasets.load_diabetes()X=data['data']y=data['target']lr=LinearRegression()scorer='neg_mean_squared_error'rfecv = RFECV(estimator=lr, step=1, cv=KFold(5),scoring=scorer)rfecv.fit(X, y)sns.set(style='darkgrid')plt.xlabel("Number offeatures selected")plt.ylabel("Cross validationscore (MSE)")plt.plot(range(1, len(rfecv.grid_scores_) +1), -rfecv.grid_scores_,'r',label="Optimal number offeatures : %d"% rfecv.n_features_)plt.legend()plt.show()
利用包裹法我们可以挑选出最佳的特征子集包含的特征数为6,这样的特征子集的泛化能力比全部特征集要好,最佳特征子集的MSE大约为2946.88,而全部特征的MSE大约为2993,说明对数据进行特征选择可以显著提高模型的性能。我们可以通过如下代码查看哪几个特征得以保留:
np.array(data['feature_names'])[rfecv.support_]#这里面用到了numpy数组的布尔值切分方法
包裹法非常的简单粗暴,直接利用特征子集的表现来达到挑选特征的作用,但它固定了学习器,如果我们用linear regression挑选完特征,也只能说明,这些特征是在linear regression上最佳的组合,而不能放入到更广泛的模型中,比如,向量机和贝叶斯模型。
而嵌入法嵌入在了学习器里面,训练过程和特征选择同时完成,这样的嵌入避免了学习器与特征选择相分离的麻烦,因为包裹法所挑选的特征可能会随着学习器的改变而改变。
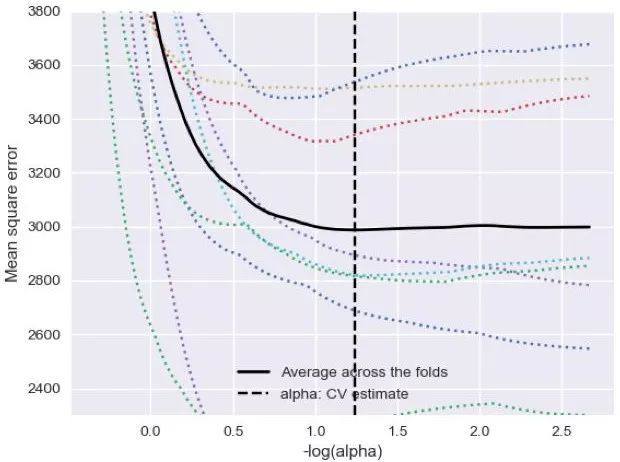
我们在《过拟合问题(代码篇)》中有过这样一幅图(最佳的
![]()
约为0.057):
表示了模型的泛化误差随着正则化系数的变化,从中选择使得泛化误差最小的.而最佳的在参数空间对应着某些特征的消失:
coefs_lasso=[]
alphas=np.linspace(0.01,0.5,1000)fora in alphas: lasso=Lasso(alpha=a) lasso.fit(X,y) coefs_lasso.append((lasso.coef_))
![]()
正则化是非常好用的办法,因为它参与模型的优化,但不依赖于模型本身,所以在很多模型中都可以嵌入它。如果它嵌入Linear Regression,就是我们前面反复讨论过的形式,可如果它嵌入了向量机,一样可以起到特征选择的作用。
从模型的角度来看特征选择,它本质就是将我们模型输入变量的维度减少,从而获得更好的性能,更快的训练速度,甚至更好的解释性。
那么还有没有其他方法可以达到类似的目的呢?我们将在下一篇介绍降维与特征选择的不同,以及我们如何恰当的应用降维。
课堂TIPS
本文的数据与《过拟合问题(代码篇)》的数据相同,主要是针对回归问题。如果是分类问题,那么过滤法中的相关系数和互信息法也要做相应的改变,我们更应该用sklearn.featureselection的fclassif和mutualinfoclassif,以及chi2。
本文采用的spearman系数法来自Scipy的统计模块。除此之外,常用的过滤法所需要的函数,在Scipy里几乎都可以找到。
从理论上来说,过滤法所剔除的特征应该与包裹法剔除的特征相同,但在实际情况中,因为数据的分布未知,过滤法的很多数学假设也就不再成立,甚至现实中的数据太过庞大,关系太过复杂,过滤法剔除的特征往往与包裹法的不同。
包裹法虽然原理简单,算法好用,但实际中特征往往很多,计算量也会变得非常大。所以正则化方法是被人普遍使用,而过滤法则往往作为一个具有参考价值的方法,并不会把过滤作为特征选择的终点。