计算几何中最基本重要的算法之一~判断线段相交基础。
只需判断线段是否同时满足
1.快速排斥实验
2.跨立实验
1.快速排斥实验:
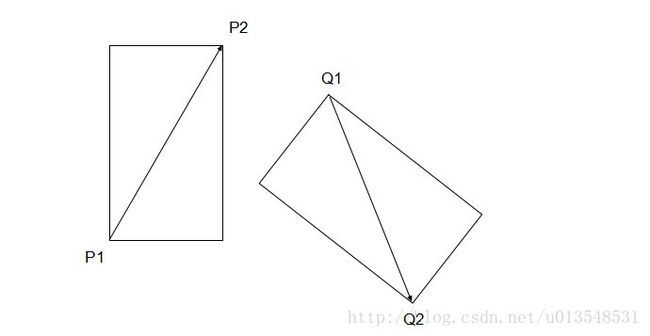
设以线段P1P2为对角线的矩形为T,以Q1Q2线段为对角线的矩形为R,那么下图这种状态时P1P2和Q1Q2肯定不相交
判断P1 P2 Q1 Q2是否满足这种关系就是快速排斥实验。
max(p1.x,p2.x) < min(q1.x,q2,x) || max(q1.x,q2.x) < min(p1,x,p2,x) ||max(p1.y,p2.y) < min(q1.y,q2,y) || max(q1.y,q2.y) < min(p1.y,p2.y)
上式为真,则表明两个矩形不想交,一般是取上式的否定,直接判断是否满足矩形相交,即。
min(p1.x,p2.x) <= max(q1.x,q2,x) && min(q1.x,q2.x) <= max(p1,x,p2,x) &&min(p1.y,p2.y) <= max(q1.y,q2,y) && min(q1.y,q2.y) <= max(p1.y,p2.y)
2.跨立实验
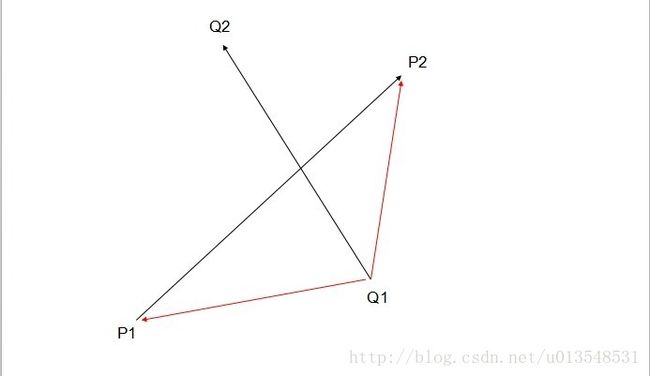
前提:如果两线段相交,必定互相跨立。
也即是说:
1.P1 P2 在Q1Q2的两侧
2.Q1Q2 在P1P2的两侧
判断两点是否在一条直线的两侧就用到叉乘了。
(Q1P1 x Q1Q2) * (Q1Q2 x Q1P2) <= 0 表示P1P2在Q1Q2的两侧
(P1Q2 x P1P2) * (P1P2 x P1Q2) <= 0 表示Q1Q2在P1P2的两侧
这就满足跨立实验的要求了~
小试一下:HDU 1086 http://acm.hdu.edu.cn/showproblem.php?pid=1086
#include
#include
//注意题目说了线段与线段之间最多只有一个交点,不存在重合或者在一条直线的情况
struct line{
double x1,y1;
double x2,y2;
};
long Judge(struct line Line1,struct line Line2)//跨立实验
{
double Xa1 = Line1.x1;
double Ya1 = Line1.y1;
double Xa2 = Line1.x2;
double Ya2 = Line1.y2;
double Xb1 = Line2.x1;
double Yb1 = Line2.y1;
double Xb2 = Line2.x2;
double Yb2 = Line2.y2;
if(((Xa2-Xa1)*(Yb1-Ya1)-(Xb1-Xa1)*(Ya2-Ya1))*((Xa2-Xa1)*(Yb2-Ya1)-(Xb2-Xa1)*(Ya2-Ya1))>0)
return 0;
if(((Xb2-Xb1)*(Ya1-Yb1)-(Xa1-Xb1)*(Yb2-Yb1))*((Xb2-Xb1)*(Ya2-Yb1)-(Xa2-Xb1)*(Yb2-Yb1))>0)
return 0;
return 1;
}
int main()
{
struct line Line[100];
int num;
while(scanf("%d",&num) != EOF && num)
{
int count = 0;
for(int i = 0 ; i < num ; ++i)
scanf("%lf%lf%lf%lf",&Line[i].x1,&Line[i].y1,&Line[i].x2,&Line[i].y2);
for(int i = 0 ; i < num - 1 ; ++i)
for(int j = i + 1 ; j < num ; ++j)
if(Judge(Line[i],Line[j]))
count++;
printf("%d\n",count);
}
return 0;
}