图像小波去噪的Matlab函数解析与并行化实现思路
此文由本人@EthanLifeGreat/@EthanUnbeaten原创，首发于CSDN。转载表明出处，感谢。
概述
本文首先介绍了一个用Matlab进行图像小波去噪的实例；然后分析了小波去噪的流程和其对应的函数，其间通俗地解释了卷积的操作、阈值化处理；最后解释了小波去噪可以并行化实现的原因，所使用的思路。
本文以一个普通理工科生能读懂的角度出发，解决了实践问题、通俗理解问题和改造问题。
对于一位想要使用Matlab进行图片的小波去噪，但又不想了解公式、原理的同学，可以重点阅读第二章；对于一位想参考小波去噪流程以及离散小波变换(DWT)原理的同学，可以重点阅读第三章；对GPU计算感兴趣的同学可以重点阅读第四章。
目录
- 概述
- 1. 简介
- 2. 如何用Matlab去噪
- 2.1. 一个小波去噪实例
- 2.2. 例子函数解析
- 2.2.1. ddencmp函数
- 2.2.2. wdencmp函数
- 3. 小波去噪的流程
- 3.1. 用傅立叶变换理解小波去噪/压缩
- 3.2. 小波分解：wavedec2函数
- 3.2.1. 函数参数
- 3.2.1.1. 输入
- 图片
- 分解层数
- 小波基/滤波器
- 3.2.1.2. 输出
- 分解系数 C
- 刻度 S
- 3.2.2 分解过程
- 3.2.2.1. 层层下分
- 3.2.2.2. wavedec2的C向量的排列
- 3.2.2.3. wavedec2的S向量的排列
- S存在的意义
- 3.2.2.4.单步分解过程
- 卷积
- 行/列卷积
- 下采样
- 单步分解总结
- 3.3. 阈值化：wthcoef2函数
- 3.3.1. 软/硬阈值化：wthresh函数
- 3.4. 小波重构：waverec2函数
- 3.4.1. 输入/输出
- 3.4.2. 层层合并
- 3.4.3. 单步合成过程
- 去边：wkeep函数
- 3.5. 小波去噪流程总结
- 4. 小波去噪的并行化实现思路
- 4.1. 通用GPU计算与CUDA框架
- 4.1.1. 通用GPU计算
- 4.1.2. CUDA架构
- 4.2. 小波分解的并行思路
- 4.3. 阈值化的并行思路
- 5. 高斯白噪声与小波变换的关系及应用
- 5.1. 独立同分布变量与高斯白噪声
- 5.2. 高斯白噪声在小波变换中的性质
- 5.3. 阈值选择
- 6. 结语
- 注脚
1. 简介
本文是作者对实习项目的过程中产生的思考的记录。
原项目需求是得到实时化(至少80fps)显示的去噪图片，这要求我们极大地缩减小波去噪的用时。 因为 Matlab 环境下的小波去噪的处理时间约是一张图5秒钟1，完全不符合我们的要求。所以我们将Matlab的函数拆解开，先用 C++ 实现，再将 C++ 代码改成 CUDA C 2 代码而成功实现了小波去噪的并行化处理（通用GPU计算）。最终的处理时间在 100 fps 左右3，满足了项目的使用需求。
在这里，我希望共享我们的思考过程。但由于版权问题，不公布项目源代码。如有建议/疑惑，欢迎留言。
同时在此感谢我的老师和两位同学，他们提供了重要的解决思路，对此文作出了重大贡献。
2. 如何用Matlab去噪
我相信你之所以能看到这篇文章，很有可能是因为你需要完成一个图像去噪的流程，而正在查阅资料。若如此，我相信这一章节会对你有帮助。
在这一章节，我们讨论怎样实现一个简易的图像去噪流程，并对其中的内容进行简要分析。读完这一章，你应该能够用 Matlab 轻松实现一个最简单的小波去噪。
2.1. 一个小波去噪实例
这个实例摘自于Matlab Support，原网页
-
wdencmp – Matlab Support
-
ddencmp – Matlab Support
% 加载图片
load sinsin; % --------- 1.加载《sinsin》图片在变量X
Y = X+18*randn(size(X)); % --------- 2.对X施加噪声得到Y
% 去噪
[thr,sorh,keepapp] = ddencmp('den','wv',Y);
% --------- 3.求解Y的全局阈值记录在thr
xd = wdencmp('gbl',Y,'sym4',2,thr,sorh,keepapp);
% --------- 4.小波去噪
% 绘图
subplot(2,2,1);
imagesc(X);
title('Original Image'); % --------- 原图X
subplot(2,2,2);
imagesc(Y);
title('Noisy Image'); % --------- 噪声图Y
subplot(2,2,3);
imagesc(xd);
title('Denoised Image'); % --------- 降噪图xd
绘图的结果在官网上是这样的：
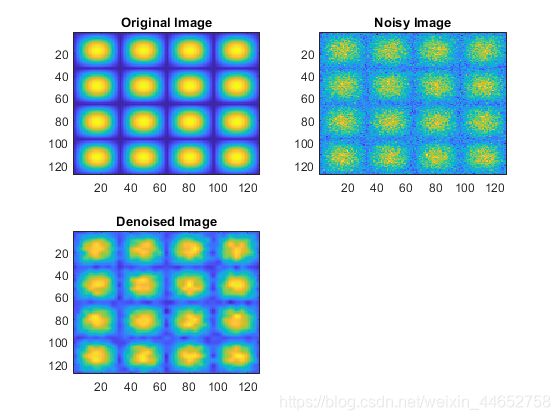
这段代码展示了一张图加噪后再进行小波去噪的结果。
实际上，要在Matlab里做到一个最简单的图像小波去噪，只需要两行代码——步骤3.和4.
步骤3.输入的三个参数意义分别是：
- ‘den’ 全称 denoise 表示去噪
- ‘wv’ 表示 小波变换
- Y 表示噪声图Y
输出的三个参数的意义是：
-
thr 全称 threshold 表示 阈值
-
sorh 全称 soft or hard 表示 硬/软降噪
-
keepapp 表示是否对分解出来的低频系数也降噪
以上三个参数都是中间过程量，如果你的目的只是会用，那么可以无视这三个解释。
步骤4.输入的前四个(后三个与3.输出的一模一样)参数意义是：
- ‘gbl’ 表示全局降噪，意味着分解出来的每一层使用的阈值都一样。也意味着thr只是一个数（而非向量）。
- Y 依然表示噪声图Y
- ‘sym4’ 表示小波基类型，有多种可选——参见Wavelet manager.
- 2 表示进行两层分解后去噪
2.2. 例子函数解析
下面我们来讲解一下这两位“集大成者”——ddencmp函数和wdencmp函数：
2.2.1. ddencmp函数
Default values for denoising or compression｜去噪/压缩默认值
ddencmp在Matlab Support上的函数描述如下：
ddencmp returns default values for denoising or compression for the critically sampled discrete wavelet or wavelet packet transform.
正如前面解释过的函数输出一样，这个函数返回的是小波去噪/压缩的默认值（阈值、硬/软降噪、是否对分解出来的低频系数也降噪）。
在这里我们不细致地解析这些值是怎么得到的。我们可以先看看Matlab官方文档给出的文献:
[1] Donoho, D. L. “De-noising by Soft-Thresholding.” IEEE Transactions on Information Theory, Vol. 42, Number 3, pp. 613–627, 1995.
[2] Donoho, D. L., and Johnstone, I. M. “Ideal Spatial Adaptation by Wavelet Shrinkage.” Biometrika, Vol. 81, pp. 425–455, 1994.
[3] Donoho, D. L., and I. M. Johnstone. “Ideal denoising in an orthonormal basis chosen from a library of bases.” Comptes Rendus Acad. Sci. Paris, Ser. I, Vol. 319, pp. 1317–1322, 1994.
肤浅地看，这些文章都是这个叫DDL的人（作为第一作者）写的 （DDL可还行） 。官方文档里也提到了：
Use ddencmp to obtain the default global threshold for wavelet denoising. Demonstrate that the threshold is equal to the universal threshold of Donoho and Johnstone scaled by a robust estimate of the variance.
官方算出了一个值，并与ddencmp得到的值作对比，说明了这个算出来的 D&J的全局阈值 的计算过程。
在本文的并行化思路里，我们不讨论怎么得到阈值，不讨论怎么并行化计算阈值的步骤——我们假定阈值已经得到，并行化其他部分。
结语：ddencmp 函数通过给定的算法从原噪声图中计算出全局阈值、软/硬法和是否处理低频系数。但至于是怎么计算的，是否满足你的需求，还请参考文献。
2.2.2. wdencmp函数
Denoising or compression｜(小波)去噪或压缩
这个函数的全称叫 Wavelet DeNoise CoMPress 小波去噪或压缩
在官方文档里有这么一句话
[XC, CXC, LXC, PERF0, PERFL2] = wdencmp(‘gbl’, X, wname, N, THR, SORH, KEEPAPP)
returns a denoised or compressed version XC of the input data X obtained by wavelet coefficients thresholding using the global positive threshold THR. [CXC,LXC] is the N-level wavelet decomposition structure of XC (see wavedec or wavedec2 for more information).
在上面的例子里，函数返回值被简化成了一个——XC，即图片X的降噪/压缩后的图。
后面的CXC和LXC是X进行小波分解并去噪后的结果，也是降噪图的小波分解结果——在wavedec2函数页也被分别称作C和S（coefficient和scale（系数和尺度）的简称）。
后面的两个返回参数PERF0和PERFL2反映去噪的程度，但与本文关系不大，故不深入讨论。
文档里还讲了，整个wdencmp函数的思路：
The denoising and compression procedures contain three steps:
- Decomposition.
- Thresholding.
- Reconstruction.
The two procedures differ in Step 2. In compression, for each level in the wavelet decomposition, a threshold is selected and hard thresholding is applied to the detail coefficients.
即
- Decomposition 小波变换分解
- Thresholding 阈值化
（这个不是很好翻译，大概意思是对分解后的结果进行处理，我们后面再细讲） - Reconstruction 逆小波变换重构
这个函数既可以实现小波去噪也可以实现小波压缩，而两者的区别在于步骤2——在压缩中每层的阈值都不一样，而且是用硬阈值处理。
至此，我们已经大致了解了wdencmp这个函数。至于这个函数具体的实现过程，我们在下一个章节讲述。
3. 小波去噪的流程
如上所述，小波去噪的过程分三步：分解、阈值化和重构。
将wdencmp拆开其实是三个函数，分别对应前面讲的三个步骤：
- 分解 – wavedec2函数
- 阈值化 – wthcoef2函数
- 重构 – waverec2函数
所谓知其然必知其所以然，在解释函数之前，我想先简单讲讲这样做的理论依据。小波变换的理论已经有非常多的细致的论述了。如果你学过高等数学/数学分析中的傅立叶变换，我希望从傅立叶变换的角度帮你理解小波去噪。
3.1. 用傅立叶变换理解小波去噪/压缩
傅立叶变换是把函数分解成正弦函数的和，小波变换也类似。在傅立叶变换里，我们需要求正弦和余弦函数的系数 a n a_n an 和 b n b_n bn 。而在小波变换里，正弦函数和余弦函数则对应的是小波基函数。小波分解呢，求的就是这些小波基的系数。
可以想像的是，如果删掉傅立叶变换得到的部分系数，如把 n > 3 n>3 n>3 时的 a n a_n an 和 b n b_n bn 置 0， 再进行逆傅立叶变换，这个函数将变成一个肉眼可见的正弦(组合)函数。当然n取3可能比较极端，但这只是为了形象地说明问题。这样的变换就大大简化了原本的函数。
不难理解，这对于压缩而言是个极大的利好——它一个函数压缩成了 5 个系数( a 0 a_0 a0, a 1 a_1 a1, a 2 a_2 a2, b 1 b_1 b1, b 2 b_2 b2)的集合。信息量少了很多。而对于去噪而言——虽然情况有些复杂——但如果勉强认为n很大时的 a n a_n an 和 b n b_n bn 代表了噪声的指标，那么我们也完成了去噪的过程。至于为什么它们代表了噪声的指标，又是怎么代表的，可以参考其它文献。
类似的，小波去噪也是把信号/图像分解成系数，再对系数进行操作。最后再逆变换（重构），得到去噪的信号/图。
3.2. 小波分解：wavedec2函数
Wavelet Decomposition 2D ｜ 二维小波分解
本章节的所有内容，都从Matlab Support文档里展开。这些内容尚且没有中文翻译，所以我怎么讲也没问题，如果不理解这部分内容大家也可以参考原文。
3.2.1. 函数参数
先看看wavedec2函数的输入和输出：
Syntax｜语法
- [C,S] = wavedec2(X,N,wname)
- [C,S] = wavedec2(X,N,Lod,Hid)
3.2.1.1. 输入
输入参数有三个：图片、层数和小波基/滤波器。
图片
X就是图片，二维数组，灰色图像。虽然也可以是RGB真彩图，但不在本文讨论范围。
分解层数
分解层数N代表了你要求分解多少层。对于不同的小波基和不同的图片的组合，有唯一确定的最大层数。至于怎么分解，我们下面会讲。
小波基/滤波器
调用方法有两种，前面一种就是用小波基，后面一种是用滤波器分解。两者天然等价。
Lod/Hid是Low/High Pass Decomposition 的简称，意思是低/高通分解（滤波器）。滤波器英文名也叫filter，也可以（被我）译为滤镜。每一个小波基天然地对应两个滤镜——低/高通分解滤波器（当然也对应两个重构滤波器），可以用这个函数得到：
[LoD,HiD,LoR,HiR] = wfilters(wname)
这些滤波器中的每一个都是一个一维数组，其中的值有正有负。
3.2.1.2. 输出
输出有二：C和S
分解系数 C
C实际上是coefficient（系数）的简写，正如上一章提到的，这些系数就类似于傅立叶变换里的 a n a_n an 和 b n b_n bn . 我们的目标是对这些系数进行处理后，再重新组合出图像。
为了方便保存，C被设定成了一个一维数组；而后面要讲的S，则是用于描述这个分解系数是如何存放的。
刻度 S
S是 scale 的简写，scale有很多的翻译方法：尺度、刻度、规模……但似乎都没能很好地描述这个S的作用——记录C中内容的存放规律。（如果你知道更好的翻译，请分享在留言区里）
事实上，官方文档里面说这是一个
Bookkeeping matrix.
簿记矩阵.
意义就是表示C里面的东西都：哪部分是干什么用的。
3.2.2 分解过程
3.2.2.1. 层层下分
正如前面所言，我们可以对图片分解很多层。每一层都由数张的图片组成。
我们还是用Matlab官方的图来说明：
原图：
第一层分解结果：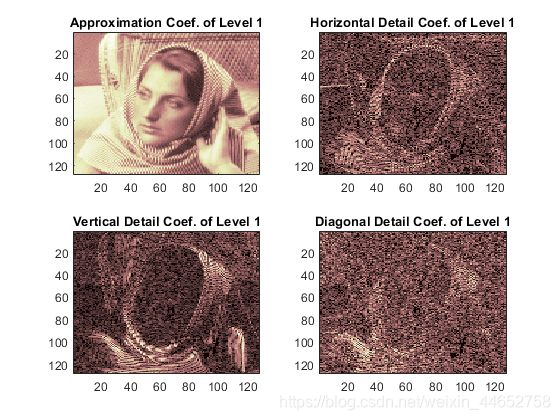
这是一张名为woman的图片在haar小波基下的第一层分解。分解后的图片变小了；原图的尺寸是 256 x 256，分解后的四张图大小都是 128 x 128.
直观地看，这四张图中只有左上角的 Approximation Coefficient （近似系数，简称A）和原图最像。右上角、左下角和右下角分别称为 水平细节（H）、垂直细节（V）和对角细节（D）
问题来了：这只是第一层分解，那要再往下分解怎么分呢？下一步，我们只分解和原图最像的A. 结果如下（还是官网原图）：
是不是又小了一圈？变成 64 x 64 了吧:)
所以聪明的你已经发现了规律——每一次将图分成四个小图AHVD，下一层分解只分解A，重复操作就可以一层层分解了！操作流程可以简化如下（依旧是官网的原图）：
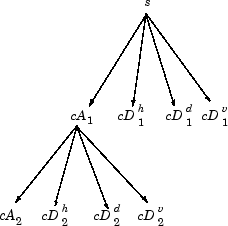其中s表示原图； c A n cA_n cAn表示第n层的A； c D n h cD_n^h cDnh表示第n层的H；D和V以此类推。
知道了层次过程，我们接着就来解答之前留下的一个疑问——C中的元素到底是怎么排列的，以及S是怎么指导它们排列的。
3.2.2.2. wavedec2的C向量的排列
先说C，根据上面的结论，我们知道C中的(图片)元素应该有 3 N + 1 3N+1 3N+1 个/张（N表示最大分解层数，下同）。在Matlab存储时从左至右是这么排列的：
A(N), H(N), V(N), D(N), H(N-1), V(N-1), D(N-1), …, H(1), V(1), D(1)
其中的A(k)等价于上图的 c A k cA_k cAk；H(k)等价于 c D n h cD_n^h cDnh；D和V以此类推。
这就是C的排列方式。注意，这里C是一个行向量，而且每一个AHVD也都是行向量。你可能会感到奇怪；这AHVD不都是图片么？怎么合起来变成一维行向量了？其实是为了方便存储，把它们按照列优先的方式(Matlab固有方式)排列成了一维的向量。
（其实我之所以没有统一AHVD的表达，是因为官网真的给出了这些不同的表达方式；更过分的是，后面还有一种表达方式。所以，读者应自己对AHVD产生清晰的认识:）
3.2.2.3. wavedec2的S向量的排列
现在看S向量，在灰度图中，它是一个二维向量/矩阵，大小是 (N + 2) x 2.
其中N表示分解的总层数。宽度 2 表示每一层图片的长、宽两项；N + 2 项表示原图、N层的H V D、最深层A共 （1 + N + 1 = N + 2）项。具体表示见下图。
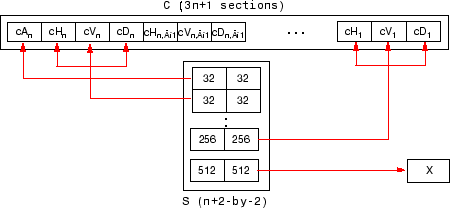
这张图展示了一个原大小为 512 x 512 的灰度图，分解 4 次至 32 x 32 大小时产生的 S 向量。箭头代表该行指向的图片的大小。
S存在的意义
看到这里，带着思考的你很可能会问：S存在的意义是什么？
我想说的是，如果我现在有一个已经算出来，排列好的C向量。那么（只要同一层的AHVD的大小总是相同，）我是不是只需要知道分解的层数和最小的A/H/V/D的大小，就可以恢复出原图呢？
如若真是这样，那我的S可以直接简化为 “层数 + A的大小” 一共三个信息量。（注意，整个分解完的C里面只有一个A矩阵，所以A在这里不引起歧义）
明明只需要3个数字，那为啥Matlab还要费心做一个这么大的矩阵，把每一层图片大小都记录下来呢？
如果你也有这样的疑惑，不妨设想一下，我们以上图为例，如果原图片不是 512 x 512，而是 513 x 513 呢？那么此时所有的分解结果都不变(分解结果向下取整)，所以重构的时候就自然恢复出了 512 x 512 的图片。当然你可能会说：那有什么关系？不就是少了一行一列嘛，我这么大一张图，损失这么点可以接受。那我们再换成 511 x 511 来分解 4 层，过程我就不展示了，留作课后作业大家完成。 恢复出来的结果是 496 x 496。还能接受么？
当然你可能会说世界上哪有 511 x 511 这么吊诡的图片？
作为一名数学系学生，我反正不能接受；作为一个成熟的商业软件，Matlab 亦不能接受。
所以，保留每一层分解的图片大小是完整恢复原图的必要条件。这就是S存在的意义。
3.2.2.4.单步分解过程
现在我们已经知道了，每次分解出新的一层，都是对A进行一通操作，得到四张“小图片”。那么，究竟怎么分出四张图呢？
作为一篇普通理工生也可以读懂的文章，这里不讨论数学公式，只讲实操。
“首当其冲”地，还是官方的图：
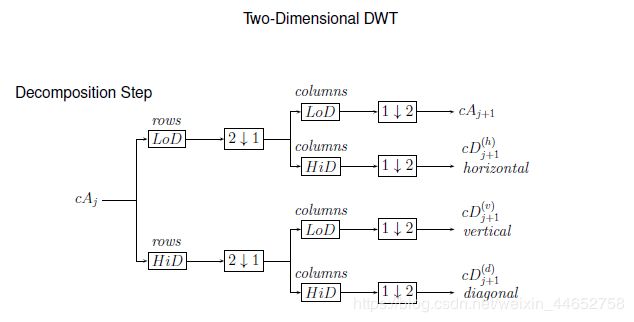
有了前面的知识铺垫，你应该能够清楚地认识到：这个图表示的是，第 j 层的 A，通过一通操作变成了 第 j + 1 层的 AHVD.
直接讲有点麻烦，我们还是看一下官网的图例：
对应着翻译过来就是（符号我就不画了）：
其中
- 对列下采样：保留偶数序数的列
- 对行下采样：保留偶数序数的行
- 用滤镜 X 对行进行卷积
- 用滤镜 X 对列进行卷积4
所以按照先后顺序，一个A要经过一次卷积、一次下采样、一次卷积再一次下采样得到下一层的 A/H/V/D.
接下来我们就讲讲，什么是个卷积，什么又是个下采样。
卷积
如果你学过Deep Learning(深度学习)，那么你一定对卷积这个词再熟悉不过了；但对于某些曾被DL劝退的人而言，我们仍需进行一些简单、通俗的解释。
在这里，我们不需要知道卷积是做什么的5，也不需要知道为什么要做卷积，我们只需要知道这个卷积是怎么完成的就可以了。
我从他人的博客上借鉴了这张图：
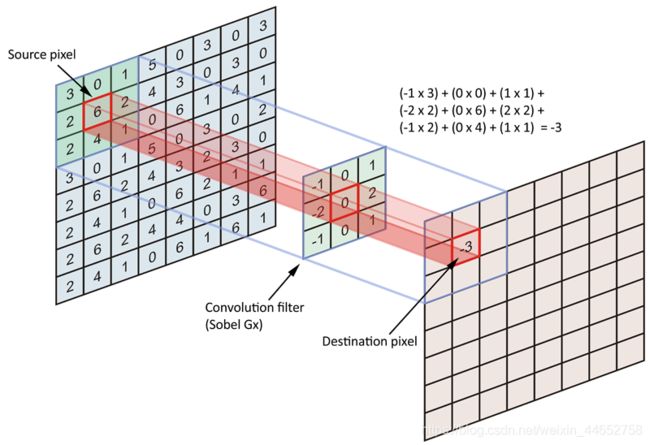
图中最左边的矩阵是原图，中间的小矩阵是所谓的滤镜filter，最右边是卷积结果图。这张图展示的是滤镜中心0对准原图中的数字6时得到的结果-3，然后九个位置的九对数字分别相乘，作和（如图中式子）结果写在结果图中对应(原图的6)的位置。
任由滤镜在原图上滑动，并进行如上的作和操作。我们可以想像，数字可以填满结果图中的每一个空——除去最外面的一圈。这是卷积的天然特性；结果图总比原图小。那怎么办呢？
好办，我们事先把原图像扩大一圈，再做卷积，就可以保证结果图和原图一样大了。好想法，那么我们怎么扩大呢？
有许多办法，最简单的有两种：
- 零延拓(Matlab: zpd)
将要填充的边界全部写成0 - 对称延拓(Matlab: sym)
将边界当作对称线，顶点当作对称点扩大图像
行/列卷积
上面我们简单讲了卷积的操作。但wavedec2函数里说的按行/列卷积又是什么样的呢？
还记得我们刚讲滤镜的时候说过，wavedec2里的每个滤镜都是一个一维数组吧。所以其实按行/列卷积的意思就是：把滤镜横/竖着卷积。
对于按行卷积，我做了一个简单的示意图：
这张动图展示了：原图 8 x 8大小，滤镜长度3，原图填充后行卷积的例子。深蓝色线条表示对应位置相乘，浅蓝色线条表示作和，与上一张图中显示的计算过程类似。
列卷积类似（列填充，滤镜竖直）。
在这个例子里，每一次卷积的输出结果应是与延拓前矩阵大小相同的矩阵。即保证输出与输入图片大小相同。
至此，我们已经讲完了wavedec2里卷积的部分。现在来讲讲下采样。
下采样
尽管其正当性一言难尽，但行/列下采样操作起来十分简单；保留偶数序数的行/列，丢掉剩余的行/列。
所以一个大小为 512 x 512 的图经过一次列的下采样，大小就变成了 512 x 256. 一张这样大小的图，经过一次行的下采样，就会变成 256 x 256 大小。形象直观。没有更多的解释余地。
单步分解总结
单步分解把某一层的A（最初为原图）分解成下一层的AHVD.
其步骤是：
- 行卷积
- 列下采样
- 列卷积
- 行下采样
从由于卷积核/滤镜的不同，使得分解的结果不同：
- 如果两次均为低通，得到A图；
- 如果先低通后高通，得到H图；
- 如果先高通后低通，得到V图；
- 如果两次均为高通，得到D图。
至此，我们已经讲完了wavedec2函数以及小波分解的实际操作流程。下面我们介绍小波去噪的核心程序：阈值化。
3.3. 阈值化：wthcoef2函数
Wavelet coefficient thresholding 2-D ｜ 小波系数阈值化2D
阈值化虽说是去噪的核心，但实现起来非常简单。就是对分解得到的系数进行修改，用给定的阈值来修改。
wthcoef2函数所做的事情其实只有两件：
- 找到需要修改的部分系数
- 用相应的阈值修改这部分系数(调用wthresh函数)
首先是找到需要修改的部分系数，下面是对最常用的一个输入的解读。
NC = wthcoef2(‘type’,C,S,N,T,SORH)
For ‘type’ = ‘h’ ( ‘v’ or ‘d’), NC = wthcoef2(‘type’,C,S,N,T,SORH) returns the horizontal (vertical or diagonal, respectively) coefficients obtained from the wavelet decomposition structure [C,S] (see wavedec2 for more information), by soft (if SORH =‘s’) or hard (if SORH =‘h’) thresholding defined in vectors N and T. N contains the detail levels to be thresholded and T the corresponding thresholds. N and T must be of the same length. The vector N must be such that 1 ≤ N(i) ≤ size(S,1)-2.
‘type’ 可以输入三种字符 ‘h’, ‘v’, ‘d’，分别表示对给定C中的所有H/V/D进行处理；C和S是我们的老朋友了，wavedec2得到的结果；N和T是等长的一维数组，N表示要处理的层数（第几层），而T表示N对应的层数对应的阈值；SORH表示软/硬处理。
N和T的这种给人留了很多想象的空间，在这里我展示一种常见的调用方法；对于分解了 6 层的系数，N和T可以这样表示：
N = [1, 2, 3, 4, 5, 6];
T = [310, 305, 300, 295, 290, 295]; % 这里的六个系数是随便取的，不具有实际内涵
一旦确定了要处理的部分，与其对应的阈值，wthcoef2就会依次调用wthresh函数进行软/硬阈值化处理。
3.3.1. 软/硬阈值化：wthresh函数
Soft or hard thresholding｜软或硬阈值化
通俗意义上我们将阈值理解为一个最小值。比如听觉阈值，指的是能听见最小声音的分贝数。
在去噪里，类似地，我们把低于最小值（阈值）的系数去掉（置为0）；而对于大于阈值的系数：
- 如果保持不变就是硬阈值化
- 如果减去阈值就是软阈值化
为什么软阈值化要将原来的值减去阈值呢？看看Matlab官方的这张图就能理解了。
在这张图里，阈值为 0.4，两种处理结果中原信号低于0.4的部分都变成了0。此外，软处理还把大于0.4的部分都减去了0.4，这维持了原信号的光滑度，故称为软处理。
软阈值化是为了“小波域产生突变，导致去噪后结果产生局部的抖动”(百度知道)。
硬阈值化更适用于图像压缩；把系数置为0的目的是减少信息量。而对大于阈值的部分不做处理是为了与原图更相近。
//下面展示一个图像小波变换软/硬阈值化后的区别：
3.4. 小波重构：waverec2函数
2-D wavelet reconstruction｜2维小波重构
有了前面的铺垫，再讲重构就很简单了；小波重构是小波分解的逆过程。在Matlab Support上有一个例子。在这个例子中，作者对woman这张图片先进行wavedec2分解，之后直接以同样的参数进行waverec2重构，并对两张图片进行对比。结果显示，两张图对应像素的差异的最大值只有2.5565e-10
3.4.1. 输入/输出
我们还是简单了解一下这个函数的调用方式吧：
X = waverec2(C,S,wname)
X = waverec2(C,S,Lo_R,Hi_R)
通过小波基或者高、低通滤镜对C和S操作合成出图片；
- C：C既可以是阈值化后的也可以是没有经过阈值化而刚分解的C
- S：S一直都是wavedec2分解出来的S，没有改变
- wname：小波基
- Lo_R/Hi_R：低/高通合成滤镜，也是由小波基唯一决定的
提示：分解滤镜和合成滤镜其实是同一组数据的互反：
还是用官网的图片来说明：
这张图展示了db5的四个滤镜（四个一维数组）中数字的大小。
可以明显地看出来：低通滤镜LoD和LoR两个数组中的元素是一样的，但是顺序恰好完全颠倒。高通滤镜亦如是。
这也是我选择将filter翻译为滤镜而非滤波器的原因之一；这些数组就像是一面透镜，图片从一面穿向另一面时被分解，回穿时被组合。
3.4.2. 层层合并
整体上，与分解的宏观过程相反：重构是从最深层把每一层的A/H/V/D组合起来，形成上一层的A。并重复这个过程，直到恢复到“第0层”。
3.4.3. 单步合成过程
那么单步具体怎么合成呢？类似地，我们来看看它的流程图，同样摘自官网.
还是解释一下原图里的图例（依次翻译）：
- 列上采样：在奇序数列处填0
- 行上采样：在奇序数行处填0
- 行卷积：用滤镜X对行卷积
- 列卷积：用滤镜X对列卷积
你应该能注意到，在最后，我们多出了一个分解中没有的流程——wkeep函数。它又是做什么的呢？
去边：wkeep函数
Keep part of vector or matrix｜部分保留向量/矩阵
看看这个简介，话语中就透露着稚气。是的，对比前面的那些函数，这算是最简单的函数（之一）了。我们只用一个例子来解释：
% For a matrix.
x = magic(5)
x =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
y = wkeep(x,[3 2])
y =
5 7
6 13
12 19
在这里，wkeep保留了这个矩阵中最中间的3行2列。
3.5. 小波去噪流程总结
至此，我们已经完整地分析了小波去噪的流程：
- 将图片通过离散小波变换分解为系数
—— 对应 wavedec2 函数 - 对系数进行修改（阈值化）
—— 对应 wthcoef2 函数 - 将修改后的系数重新组合为图片
—— 对应 waverec2 函数
下面，我们将进入小波去噪的并行化思路的介绍。
4. 小波去噪的并行化实现思路
这一章简单讨论小波去噪并行化的思路与我们选择的方向。
4.1. 通用GPU计算与CUDA框架
什么是并行化？什么是GPU？什么又是通用GPU计算？什么又是CUDA？
4.1.1. 通用GPU计算
我从别人的博客里搬了一段话：
GPU英文全称Graphic Processing Unit，中文翻译为”图形处理器”。GPU从诞生之日起就以超越摩尔定律的速度发展，运算能力不断提升。业界很大研究者注意到GPU进行计算的潜力，于2003年SIGGRAPH大会上提出了GPGPU(General-purposecomputing on graphics units)的概念。GPU逐渐从由若干专用的固定功能单元(Fixed Function Unit)组成的专用并行处理器向以通用计算资源为主，固定功能单元为辅的架构转变。
————————————————
版权声明：本文为CSDN博主「fengbingchun」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/fengbingchun/article/details/19619491
简单但不那么精确地说，就是：以前用来作图形显示的所谓“显卡”6，今天被拿来当成计算器了。而且效果还不错。然后这种起计算作用的GPU就叫做通用GPU。
那为什么GPU（有些时候）效果就值得比CPU好呢？我大i9它不香么？ 其实是各有所长罢了。我们先用一张图来理解这个事情：
蓝色的是CPU的计算核心，绿色的是GPU的计算核心（此处数量不代表真实数字）。此图想表达的是：CPU核心少，但每个核心的计算能力相当强大；GPU核心多，但每个块儿的计算能力相当单薄。
我曾经听过一个我认为很贴切的比喻：
CPU是一个老教授，积分微分都能干；GPU是一群小学生，每个人能力有限，但数量庞大。
很多情况下也可以用搬砖做比喻的话那就是：一个大力士与一群瘦竹竿。在砖的数量很多时，你肯定愿意选一群人来帮你搬砖，尽管每个人一次搬的量要少一些。等会我们会看到：做卷积就是类似于这种搬砖的过程。
概括性地讲：CPU做事效率高，但得一件一件接着做（串行处理）；GPU做事效率一般，但可以成百上千件事同时干（并行处理）。
4.1.2. CUDA架构
我们刚才讲了，某些时候GPU可以替代CPU做计算，这被称为通用GPU计算。
CUDA架构则允许我们用类C语言对（NVIDIA的）GPU进行编程，使之用于计算。这样的类C语言被称为CUDA C或C的CUDA拓展。
刚才说了，通用GPU计算有一个通俗的比喻是：指挥一群人搬砖。但问题是，怎么指挥？CUDA提供的办法是：
编号。 每个工人对应一个号码比如1-100。而我们有10000块砖需要从A地搬到B地，我们分别对砖块也标记上1-10000。然后我们下令：每个工人将所有编号为 自 己 编 号 + k ∗ 100 自己编号+k*100 自己编号+k∗100的砖从A地搬到B地，其中k取0到99。
在这里，砖块上的号码就叫做“线程号7”。有10000块砖就有10000件事等着做8，就有10000个所谓的“线程”。至于安排多少个工人来做，工人们又是怎么编号的，那是GPU来决定的，咱不用管。
实际上，CUDA C编程要比这个比喻复杂得多。篇幅有限，我们就不再赘述。有兴趣的话可以参考NVIDIA的官网以及其它的CUDA编程教程。
4.2. 小波分解的并行思路
小波去噪的三过程：分解、阈值化和重构。由于分解和重构极其相似，我们只讨论分解就够了。
还记得我们之前讲过的小波分解的流程吧。
按照先后顺序，一个A要经过一次行卷积、一次下采样、一次列卷积再一次下采样得到下一层的 A/H/V/D.
直观上看，想要并行化处理，那就要在卷积上做文章（也似乎只有卷积可以做文章）。
卷积的本质是：将一张图的部分与滤镜对应相乘再作和，得到结果图中的一个像素点。所以回顾我们的工人比喻，我们可以将结果图中的像素点进行编号。这样一来，每一个线程的工作（搬砖工作）就是：把指定位置的原图部分和滤镜对上，对应位置相乘后全部加起来，用算式描述：
R ( x , y ) = Σ l e n ( f i l t e r ) ( S A i ∗ f i l t e r i ) R_{(x,y)} = \Sigma_{len(filter)} (S_{A_i} * filter_i) R(x,y)=Σlen(filter)(SAi∗filteri)
其中R表示卷积结果图，filter表示滤镜，len()表示取长度，S表示原图，i表示滤镜上的位置，A是某种映射函数。
现在我们已经直到卷积怎么并行化了。但还有一点值得说明：
行卷积之后是有行下采样的！也就是说，如果你第一次卷积的时候把所有行都做了卷积。哈哈，那你多浪费了一倍的时间；你做出来的结果有一半都是多余的，马上要被丢掉的。所以说，不论是行卷积还是列卷积，只要有选择性地做（隔着行/列）就可以了。
事实上，这个问题并不是并行化的问题。不论在何种架构里，这部分卷积过程都是多余的。不知道Matlab有没有发现这个事情呢？:B)
4.3. 阈值化的并行思路
最后一部分是阈值化的并行，这一部分的简单来自于阈值化这个函数的简单。（这句话里流露出作者对阈值化函数的蔑视，和他的孤傲心态）
在确定好了哪些部分的系数需要阈值化处理之后，把这些位置编上号丢给GPU去分配工作就好了。
5. 高斯白噪声与小波变换的关系及应用
这一章是补充更新的。时隔多月，如与前文文风不符，请见谅。
高斯白噪声是较常见的加性噪声，本章希望通过阐述该噪声在小波变换下的特性，导出一种可能的面向高斯白噪声的噪声阈值选取办法。
本章理论推导主要集中于一维信号，但不难推广至二维信号（图像）。在最后一节我们给出二维中的结论。
5.1. 独立同分布变量与高斯白噪声
对于若干随机变量，若他们的取值相互独立，并且服从同一分布，则称之为独立同分布(i.i.d.)变量。
高斯白噪声是一种采样点取值服从独立同分布的信号。独立意味着信号在某一时间点的取值与其它时间无关，这对应了“白”的性质9。同分布指同高斯分布，这种分布是自然界中最为常见的分布。
5.2. 高斯白噪声在小波变换中的性质
（一维）高斯白噪声经过小波变换后，在两个子信号中的能量一致，并与变换前的能量一致。这一点可以简单验证——白噪声频谱平坦，故高通滤波和低通滤波的结果能量一致。
利用正态随机变量线性组合的性质我们可以给出证明。
证明：假设某一小波变换的支撑长度为4（不失一般性），原信号S中的点记作 S i S_i Si，满足 S i S_i Si ~ ( 0 , σ 2 ) ( 0,\sigma^2) (0,σ2). 由概率论中正态随机变量线性组合的性质知道，变换后趋势子信号的任意一点的值为
在这里， α i \alpha_i αi是前面章节提到的滤波器的系数，满足 Σ α i 2 = 1 \Sigma \alpha_i^2=1 Σαi2=1的性质。
不难发现其同样满足 N ( 0 , σ 2 ) N ( 0,\sigma^2) N(0,σ2)的性质，同样地，可以证明波动子信号的分布也保持不变。
这与其它一般信号（包括语音、音乐、图片等）能量集中在低频不同，因此，可以通过小波变换把噪声在波动子信号（相对）独立地展现出来。
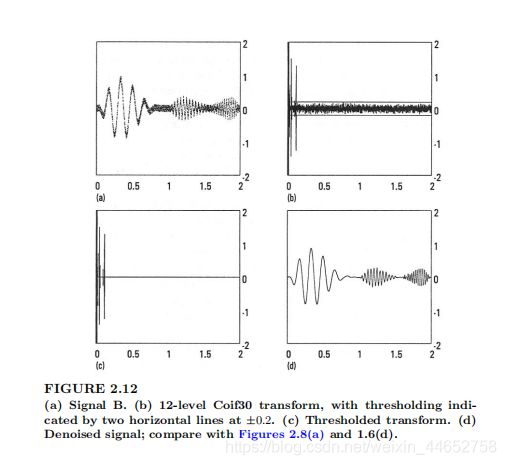
上面这张图（源自《A Primer on Wavelets and their Scientific Applications》）展示了一个带高斯白噪声信号经12层小波变换后的样子(b)，可以看到噪声依然集中在整个区域内，但是原来信号中主要的内容已经集中到趋势子信号(前面讲的近似系数A，图片中左侧部分)。
因此可以对右侧的噪声进行估计，选取阈值。
5.3. 阈值选择
由于高斯白噪声经过变换还是高斯白噪声 （你大爷还是你大爷） ，而纯净信号的主要能量已经集中到近似系数里了。
所以，可以把阈值设置在高斯白噪声的 4 σ 4\sigma 4σ处。就概率而言，噪声振幅大于此处的部分占比仅为0.01%。
因此，对细节信号（对角细节/波动子信号）进行标准差计算，最后将阈值设为4个标准差左右即可。
当然，这么做显然不是十全十美的。因为纯净部分的信号经过变换也会有一部分出现在细节信号里，它们很容易被噪声淹没。这会带来两个问题：
一是这些细节可能将永远无法恢复，所以对含噪信号去噪，近似等于对原信号低通滤波；
二是这些细节影响标准差的计算。如果要避免影响的发生，则需要先验知识，例如——确信某一小部分细节信号的纯净部分很小至可以忽略时，只对这一部分细节信号进行标准差估计即可。正如“细节”这个描述一样，这样的区域可以选在原图/原信号中非常光滑、没有波动、没有什么细节的地方。
6. 结语
本文从通俗的角度介绍了图像小波去噪的实例，解析了三个函数，最后对这三个函数的并行化实现进行了简要分析。目的在于给非专业同学一些启发性的参考。
注脚
图像2k大小，需要6层分解 ↩︎
显卡厂商NVIDIA推出的运算平台 ↩︎
使用 NVIDIA GeForce GTX1080Ti ↩︎
这里原文把列打成了行，翻译后已修正。 ↩︎
“但我就是想知道”：在DL里，卷积是为了“抽取特征”；在这里，卷积是为了完成离散小波变换(DWT)的功能。 ↩︎
这里的“显卡”应为“GPU”；“GPU”不等于“显卡”，GPU是显卡的核心，显卡还包括显存等其它组件。 ↩︎
这里的线程号不同于操作系统里的线程号。CUDA的线程称为“硬件线程”。 ↩︎
（假定一次只能搬一块砖，并计作一件事) ↩︎
白的意思是频谱的振幅（在概率上）是恒定的，与有色噪声相对。 ↩︎