一篇文章带你快速入门 DFS抽象深度优先搜索——C++实现
因博主水平确实有限,写文章确实费时费力,如果对你有帮助,请点赞支持!感谢!感谢!感谢!
因博主水平确实有限,写文章确实费时费力,如果对你有帮助,请点赞支持!感谢!感谢!感谢!
因博主水平确实有限,写文章确实费时费力,如果对你有帮助,请点赞支持!感谢!感谢!感谢!
深度优先搜索(DFS):
深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
深度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
框架展示:
例一、K个数的和
题目描述:
给定n个整数,要求选出K个数,使得选出来的K个数的和为sum。
输入:
第一行为给定整数的数量n,要求选出整数的数量K,选出来的K个数的和sum
第二行依次输入n个给定的整数
输出:
满足条件的方案数
思路:
对每一个数,枚举选或者不选两种情况,并且使用dfs来完成此枚举过程。
此过程中用S记录当前选择的数值总和,k记录选择的数的个数,deep表示当前正在枚举第几个数是否选择
对每一层,我们都有两个选择——选和不选。不同的选择,都会使得搜索进入完全不同的分支继续搜索。而每个状态对应的子树,都是这个状态通过搜索可能达到的状态。
代码一如下:
#include
using namespace std;
int n,k,sum,ans;
int a[40];
void dfs(int i,int cnt,int s){
//i为当前正在选取第i个数,cnt表示选取了几个数,s表示选取数的和
if(i==n){
if(cnt==k&&s==sum){
++ans;
}
return;
}
dfs(i+1,cnt,s);
dfs(i+1,cnt+1,s+a[i]);
}
int main(){
cin>>n>>k>>sum;
for(int i=0;i>a[i];
ans=0;
dfs(0,0,0);
cout< 代码一运行结果:
代码二如下:
#include
using namespace std;
int n,k,sum,ans;
int a[40];
bool xuan[40];
void dfs(int s,int cnt){
if(s==sum&&cnt==k){
++ans;
}
for(int i=0;i>n>>k>>sum;
for(int i=0;i>a[i];
ans=0;
dfs(0,0);
cout< 代码二运行结果:
代码二出错原因:
这里出现了重复!运行结果为正确结果的K!倍。
为什么呢?原因在于这段代码,将只是方案中元素排序顺序不同的相同的方案重复计入方案总数。
例如:(2,3,4)(2,4,3)(3,2,4)(3,4,2)(4,2,3)(4,3,2)。
那么如何解决呢?其实只需要将方案总数除以/K!即可。
DFS总结:
我们可以根据搜索状态构建一张抽象的图,图上的一个顶点就是一个状态,而图上的边就是状态之间的转移关系(进一步搜索或者回溯)。虽然dfs实在这张抽象的图上进行的,但我们不必把这张图真正地建立出来。
我们可以认为,一次dfs实际上就是在搜索树上完成了一次深度优先搜索。而在上节中的搜索树里的每一个状态,记录了两个值—和值和个数。
例二、等边三角形
题目描述:
有一些小木棍,长短不一,想用这些木棍拼出一个等边三角形,并且每根木棍都要用到。
例如有长度为1,2,3,3的4根木棍,可以让长度为1,2的木棍组成一条边,另外2根分别组成两条边。拼成一个边长为3的等边三角形。
输入:
第一行输入木棍数量n(3<=n<=10)
第二行输入n根木棍的长度
输出:
如果可以拼出等边三角形,输出“yes”,否则输出“no”。
代码如下:
#include
int n,sum=0;
int p[15];
bool f;
bool visited[15];
void dfs(int cnt,int s,int st){
//
if(f){
return;
}
if(cnt==3){
f=true;
return;
}
if(s==sum/3){
dfs(cnt+1,0,0);
return;
}
for(int i=0;i 运行结果:
例三、方程的解数
题目描述:
求解一个n元的高次方程:
输出:
方程的整数解的个数
代码如下:
#include
int k[5],p[5];
int n,M,ans;
long long poww(int x,int y){
long long ret=1;
for(int i=0;i 运行结果:
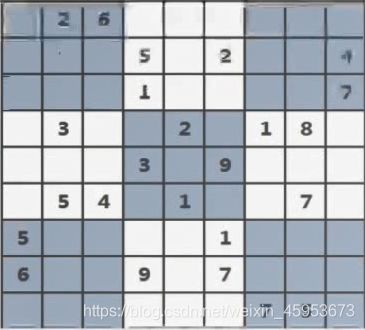
例四、数独
题目描述:
标准数独是由一个给予了提示数字的9*9网格组成,我们只需要将其空格天上数字,使得每一行、每一列以及每一个3*3宫都没有重复的数字出现。
输入:
一个 9 * 9 的数独,数字之间用空格隔开。*表示需要填写的数字。
输出:
输出一个 9 * 9 的数独,把输入中的*替换成需要填写的数字即可。
代码如下:
#include
bool vx[10][10],vy[10][10],vv[10][10];
//vx[i][j]表示第i行数字j已占用
//vx[i][j]表示第i列数字j已占用
//vv[i][j]表示区域i数字j已占用
bool f; //是否找到一个解
char s[10][10];
void dfs(int x,int y){ //从左向右从上向下
if(f) //已找到一个解
return;
if(x==9){ //向下走出界直接输出
f=1;
for(int i=0;i<9;++i){ //输出避免填好一组解,递归尝试下一组,改变原来正确的值
for(int j=0;j<9;++j){
if(j!=8)
printf("%c ",s[i][j]);
else
printf("%c\n",s[i][j]);
}
}
return;
}
if(y==9){ //向右走出界
dfs(x+1,0); //填下一行第一个数字
return;
}
if(s[x][y]!='*'){ //非*不用填,直接跳过
dfs(x,y+1);
return;
}
for(int i=1;i<=9;++i){ //检查每个数字是否可填
if(!vx[x][i]&&!vy[y][i]&&!vv[x/3*3+y/3][i]){
s[x][y]='0'+i; //可填即填入
vx[x][i]=1;
vy[y][i]=1;
vv[x/3*3+y/3][i]=1;
dfs(x,y+1); //填下一个数字
vx[x][i]=0; //因为填入的数字可能不合法,需要回溯
vy[y][i]=0;
vv[x/3*3+y/3][i]=0;
s[x][y]='*';
}
}
}
int main(){
for(int i=0;i<9;++i){ //读入
for(int j=0;j<9;++j){
scanf(" %c",&s[i][j]); //空格吃掉空白字符
}
}
for(int i=0;i<9;++i){ //标记已使用的数字
for(int j=0;j<9;++j){
if(s[i][j]!='*'){
vx[i][s[i][j]-'0']=1;
vy[j][s[i][j]-'0']=1;
vv[i/3*3+j/3][s[i][j]-'0']=1;
}
}
}
dfs(0,0); //考虑(0,0)位置
return 0;
} 运行结果:
例五、2n皇后问题
2n皇后问题——C++详解(这篇是精髓)
例六、炸弹引爆
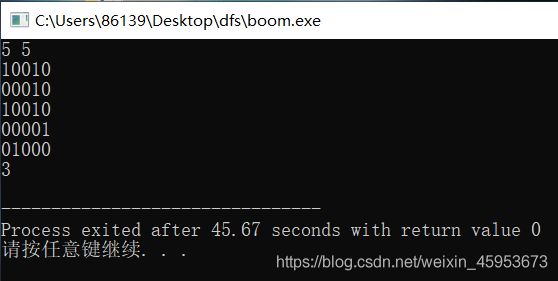
题目描述:
在一个n*n的方格地图上,某些方格上放置着炸弹。手动引爆一个炸弹以后,炸弹会把炸弹所在的行和列上的所有炸弹引爆,被引爆的炸弹又能引爆其他炸弹,这样连锁下去。
现在为了引爆地图上的所有炸弹,需要手动引爆其中一些炸弹,为了把危险程度降到最低,请算出最小手动引爆多少个炸弹可以把地图上的所有炸弹引爆。
输入:
第一行两个整数 n , m,表示地图行列数
接下来n行,每行输入一个长度为m的字符串,表示地图信息。0表示没有炸弹,1表示有炸弹
输出:
输出一个整数,表示最少需要手动引爆的炸弹数量
代码如下:
#include
int n,m,cnt;
char mp[1005][1005];
bool vx[1005],vy[1005];
//xv[i]表示第i行是否被访问,vy[i]表示第i列是否被访问
void dfs(int x,int y){
mp[x][y]='0';
if(!vx[x]){
vx[x]=1;
for(int i=0;i 运行结果:
另附:
快速入门DFS深度优先搜索