再写图像旋转算法

之前照着书写过一次，但是只按照书上的公式来编程的，至于公式怎么来的没有深究，书上讲的也不是很详细，甚至细节的部分是错误的。这次好好的研究了图像旋转算法。在这过程中网上看了好多，但是都不是太明白。然后到知网里找论文看，一篇论文图文并茂，我才真正懂了。以下是论文截图：

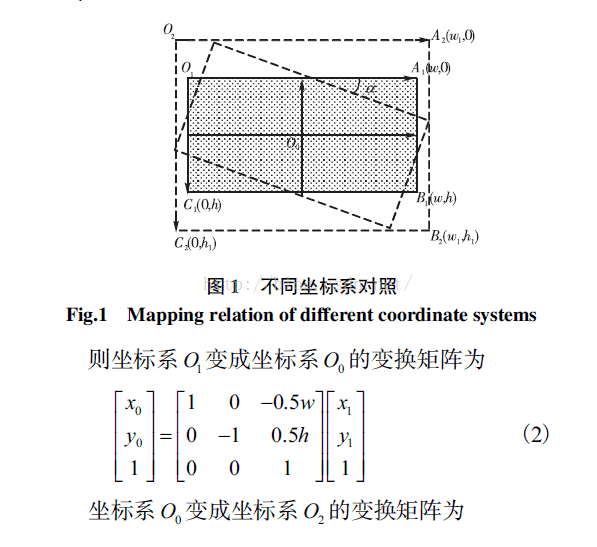
这里我总结下，首先一张图片的坐标系是O1，为了旋转，要把O1坐标系转化为O0（笛卡尔）坐标系下用旋转公式旋转，然后再把此时的O0坐标系转化为已经旋转好的新图的O2坐标系：

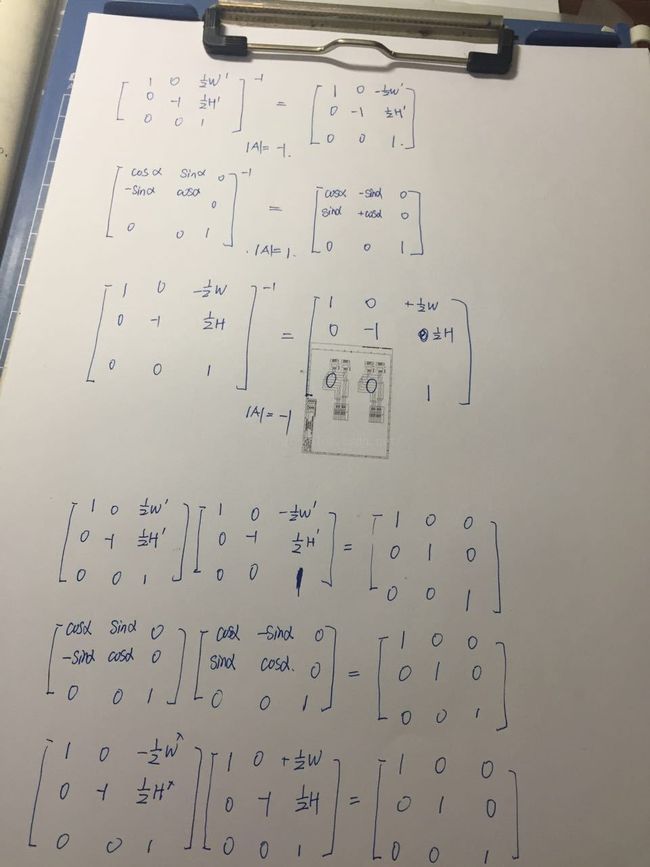
下图是我自己在草稿纸上分析的过程：

关于求逆矩阵我是问的正在准备考研的黄工的，黄工的字一如既往的清秀。一开始我硬算，算了乱七八糟的结果，真难算啊，还是求逆矩阵的好，这个简单的记住就好了，只要把副对角线变号一下就OK了。下面是黄工发来的：

好了，下面是源代码：

#include "opencv2/core/core.hpp"
#include"opencv2/highgui/highgui.hpp"
#include 
#include "iostream"
using namespace std;
using namespace cv;
#define PI 3.141592

void Rotate(Mat img ,Mat &out1,float ang)
{
	float rad=ang*(PI/180);
	int nWidth=img.cols;
	int nHeight=img.rows;

	int SrcX1=-nWidth/2;
	int SrcY1=nHeight/2;
	int SrcX2=nWidth/2;
	int SrcY2=nHeight/2;
	int SrcX3=nWidth/2;
	int SrcY3=-nHeight/2;
	int SrcX4=-nWidth/2;
	int SrcY4=-nHeight/2;

	int DstX1=(int)((cos(rad)*SrcX1+sin(rad)*SrcY1)+0.5);
	int DstY1=(int)((-sin(rad)*SrcX1+cos(rad)*SrcY1)+0.5);
	int DstX2=(int)((cos(rad)*SrcX2+sin(rad)*SrcY2)+0.5);
	int DstY2=(int)((-sin(rad)*SrcX2+cos(rad)*SrcY2)+0.5);
	int DstX3=(int)((cos(rad)*SrcX3+sin(rad)*SrcY3)+0.5);
	int DstY3=(int)((-sin(rad)*SrcX3+cos(rad)*SrcY3)+0.5);
	int DstX4=(int)((cos(rad)*SrcX4+sin(rad)*SrcY4)+0.5);
	int DstY4=(int)((-sin(rad)*SrcX4+cos(rad)*SrcY4)+0.5);

	int DstWidth=max(abs(DstX1-DstX3),abs(DstX2-DstX4))+1;
	int DstHeight=max(abs(DstY1-DstY3),abs(DstY2-DstY4))+1;

	out1.create(DstHeight,DstWidth,img.type());

	float VarX=(float)(-DstWidth*cos(rad)/2.0f-DstHeight*sin(rad)/2.0f+nWidth/2.0f);
	float VarY=(float)(DstWidth*sin(rad)/2.0f-DstHeight*cos(rad)/2.0f+nHeight/2.0f);

	for(int i=0;i(nWidth-1)||x<0||y>(nHeight-1)||y<0)
			{
				if(img.channels()==3)
				{
					out1.at(i,j)=Vec3b(0,0,0);
				}
				else if(img.channels()==1)
				{
					out1.at(i,j)=0;
				}
			}
			else
			{
				if(img.channels()==3)
				{
					out1.at(i,j)=img.at(y,x);
				}
				else if(img.channels()==1)
				{
					out1.at(i,j)=img.at(y,x);
				}
				
			}
		}
}

void main()
{
	Mat SrcImg=imread("C:\\Users\\Administrator\\Desktop\\工作\\testp\\333.jpeg",1);
	Mat RoatImg;
	Rotate(SrcImg,RoatImg,230);
	imshow("src",SrcImg);
	imshow("Rotate",RoatImg);
	waitKey();

}

效果图：

好了

但是还有一个疑问，上面的默认都是以图片中心为旋转中心，要是旋转中心在左上角呢？或在其他地方呢？又该怎么做？ 我想其中对应的矩阵需要重新推倒一下，然后算出O1->O2的对应映射矩阵就可以了，再试试看！

EN 试了，费了洪荒之力终于给折腾出来了，但是结果有点失望，因为出来的结果和之前一样！不管了，重在过程：以下的是以左上角为旋转中心

以下是源码：

int Max_four(int a,int b,int c,int d)
{
	int max=0;
	max=a>b?a:b;
	max=max>c?max:c;
	max=max>d?max:d;
	return max;
}

int Min_four(int a,int b,int c,int d)
{
	int min=0;
	min=a(nWidth-1)||x<0||y>(nHeight-1)||y<0)
			{
				if(img.channels()==3)
				{
					out1.at(i,j)=Vec3b(0,0,0);
				}
				else if(img.channels()==1)
				{
					out1.at(i,j)=0;
				}
			}
			else
			{
				if(img.channels()==3)
				{
					out1.at(i,j)=img.at(y,x);
				}
				else if(img.channels()==1)
				{
					out1.at(i,j)=img.at(y,x);
				}

			}
		}
}

效果图：

想想也是一样的，因为旋转之后的O2坐标系是随着新图变化的。