使用方向梯度直方图估计图像旋转角度
下面的代码通过计算图像中给定区域的方向梯度直方图来估计图像的旋转角度
主要内容包括:
一、计算局部图像块方向梯度直方图的函数
二、把给定图像按照给定的角度旋转
三、如何利用旋转后的图像的方向梯度直方图和原图像的方向梯度直方图来估计旋转角度
四、绘制方向梯度直方图
计算效果如下次:
主要代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 |
// LocalHistogramOfOrientedGradients.cpp : 定义控制台应用程序的入口点。
//局部方向梯度直方图
#include
#include
using
namespace
std
;
using
namespace
cv
;
/*
计算给定像素位置上的加权方向梯度直方图(orientation gradient histogram)
img:原始图像
pt: 指定的像素点
radius: 统计半径
isSmoothed:是否平滑输出直方图
用高斯函数进行中心加权;
isWeighted,和 weighted_sigma: 是否加权和计算权重的标准差
hist: 要输出的直方图
n: 直方图的bin个数
返回值:直方图的峰值(最大值)
*/
static
float
calcOrientationHist
(
const
Mat
&
img
,
Point
pt
,
int
radius
,
float
*
hist
,
int
n
,
int
isSmoothed
,
int
isWeighted
,
float
weighted_sigma
)
{
//radius应该是以pt为中心的正方形的边长的一半
int
i
,
j
,
k
,
len
=
(
radius
*
2
+
1
)
*
(
radius
*
2
+
1
);
//使用高斯函数中心加权
float
expf_scale
=
-
1.f
/
(
2.f
*
weighted_sigma
*
weighted_sigma
);
//为什么加4呢,是为了给临时直方图开辟多余的4个存储位置,
//用来存放temphist[-1],temphist[-2],temphist[n],temphist[n+1]的
//为什么加n呢,这n个位置是留给temphist[0 ... n-1]的
//为什么len*4呢,这4个len长度的数组位置是留给X、Y、W以及方向Ori的
AutoBuffer
<
float
>
buf
(
len
*
4
+
n
+
4
);
//X是横向梯度,Y是纵向梯度,Mag是梯度幅值=sqrt(X^2+Y^2), Ori是梯度方向 = arctan(Y/X)
float
*
X
=
buf
,
*
Y
=
X
+
len
,
*
Mag
=
X
,
*
Ori
=
Y
+
len
,
*
W
=
Ori
+
len
;
float
*
temphist
=
W
+
len
+
2
;
//加2是用来存放temphist[-1],temphist[-2]的
//临时直方图清零
for
(
i
=
0
;
i
<
n
;
i
++
)
temphist
[
i
]
=
0.f
;
//从上往下,从左往右扫描求横向,纵向的梯度值以及对应的权值
for
(
i
=
-
radius
,
k
=
0
;
i
<=
radius
;
i
++
)
{
int
y
=
pt
.
y
+
i
;
//指向原图像img的第pt.y+i行
if
(
y
<=
0
||
y
>=
img
.
rows
-
1
)
//边界检查
continue
;
for
(
j
=
-
radius
;
j
<=
radius
;
j
++
)
{
int
x
=
pt
.
x
+
j
;
//指向原图像img的第pt.x+j列
if
(
x
<=
0
||
x
>=
img
.
cols
-
1
)
//边界检查
continue
;
//横向梯度
float
dx
=
(
float
)(
img
.
at
<
uchar
>
(
y
,
x
+
1
)
-
img
.
at
<
uchar
>
(
y
,
x
-
1
));
//纵向梯度
float
dy
=
(
float
)(
img
.
at
<
uchar
>
(
y
-
1
,
x
)
-
img
.
at
<
uchar
>
(
y
+
1
,
x
));
//保存纵向梯度和横向梯度
X
[
k
]
=
dx
;
Y
[
k
]
=
dy
;
//计算加权数组
if
(
isWeighted
)
W
[
k
]
=
(
i
*
i
+
j
*
j
)
*
expf_scale
;
else
W
[
k
]
=
1.f
;
//如果不加权,则每个统计点上的权重是一样的
k
++
;
}
}
//把实际的统计点数复制给len,由于矩形局部邻域有可能超出图像边界,
len
=
k
;
//所以实际的点数总是小于等于 (radius*2+1)*(radius*2+1)
//在指定像素点的邻域内 计算梯度幅值, 梯度方向 and 权重
exp
(
W
,
W
,
len
);
//权重
fastAtan2
(
Y
,
X
,
Ori
,
len
,
true
);
//梯度方向
magnitude
(
X
,
Y
,
Mag
,
len
);
//梯度幅值
//填充临时直方图,直方图的横轴是梯度方向方向角度[0,360),bin宽度为n/360;
//纵轴是梯度幅值乘以对应的权重
for
(
k
=
0
;
k
<
len
;
k
++
)
{
int
bin
=
cvRound
((
n
/
360.f
)
*
Ori
[
k
]);
//求出第k个角度Ori[k]的bin索引号
if
(
bin
>=
n
)
bin
-=
n
;
if
(
bin
<
0
)
bin
+=
n
;
temphist
[
bin
]
+=
W
[
k
]
*
Mag
[
k
];
}
if
(
isSmoothed
)
{
// 直方图平滑,平滑后放入输出直方图数组中
temphist
[
-
1
]
=
temphist
[
n
-
1
];
temphist
[
-
2
]
=
temphist
[
n
-
2
];
temphist
[
n
]
=
temphist
[
0
];
temphist
[
n
+
1
]
=
temphist
[
1
];
for
(
i
=
0
;
i
<
n
;
i
++
)
{
hist
[
i
]
=
(
temphist
[
i
-
2
]
+
temphist
[
i
+
2
])
*
(
1.f
/
16.f
)
+
(
temphist
[
i
-
1
]
+
temphist
[
i
+
1
])
*
(
4.f
/
16.f
)
+
temphist
[
i
]
*
(
6.f
/
16.f
);
}
}
else
//不平滑直方图
{
for
(
i
=
0
;
i
<
n
;
i
++
)
{
hist
[
i
]
=
temphist
[
i
];
}
}
//求直方图梯度的最大值
float
maxval
=
hist
[
0
];
for
(
i
=
1
;
i
<
n
;
i
++
)
maxval
=
std
::
max
(
maxval
,
hist
[
i
]);
return
maxval
;
}
void
DrawHist
(
Mat
&
hist
,
string
&
winname
)
{
Mat
drawHist
;
int
histSize
=
hist
.
rows
;
// 创建直方图画布
int
hist_w
=
360
;
int
hist_h
=
360
;
//直方图图像的宽度和高度
int
bin_w
=
cvRound
(
(
double
)
hist_w
/
histSize
);
//直方图中一个矩形条纹的宽度
Mat
histImage
(
hist_w
,
hist_h
,
CV_8UC3
,
Scalar
(
0
,
0
,
0
)
);
//创建画布图像
/// 将直方图归一化到范围 [ 0, histImage.rows ]
normalize
(
hist
,
drawHist
,
0
,
histImage
.
rows
,
NORM_MINMAX
,
-
1
,
Mat
()
);
/// 在直方图画布上画出直方图
for
(
int
i
=
1
;
i
<
histSize
;
i
++
)
{
//矩形图表示
rectangle
(
histImage
,
Point
((
i
-
1
)
*
bin_w
,
hist_h
),
Point
(
i
*
bin_w
,
hist_h
-
cvRound
(
drawHist
.
at
<
float
>
(
i
-
1
))),
Scalar
(
0
,
0
,
255
),
1
,
8
,
0
);
//折线表示
/* line( histImage, Point( bin_w*(i-1), hist_h - cvRound(hist.at
Point( bin_w*(i), hist_h - cvRound(hist.at
Scalar( 0, 0, 255), 1, 8, 0 );*/
}
/// 显示直方图
cv
::
namedWindow
(
winname
,
1
);
cv
::
imshow
(
winname
,
histImage
);
}
int
main
(
int
argc
,
char
**
argv
)
{
const
string
filename
=
"meinv2.jpg"
;
Mat
Image
=
imread
(
filename
,
1
);
if
(
Image
.
empty
())
{
std
::
cout
<<
"无法读取图像...."
<<
endl
;
getchar
();
}
Mat
grayImage
;
//灰度图像
cvtColor
(
Image
,
grayImage
,
CV_BGR2GRAY
);
//-------------------------------计算方向梯度直方图的参数------------------------
Point
center
(
grayImage
.
cols
/
2
,
grayImage
.
rows
/
2
);
cout
<<
"原图中心点: "
<<
center
<<
endl
;
int
radius
=
120
;
//局部邻域半径
Rect
StatisticArea
(
center
.
x
-
radius
,
center
.
y
-
radius
,
2
*
radius
,
2
*
radius
);
int
bins_count
=
60
;
//bin的数目
float
sigma
=
radius
*
0.5f
;
//加权函数的标准差,设为统计区域的半径的一半
bool
isSmoothed
=
true
;
//是否平滑直方图
bool
isWeighted
=
false
;
//不加权
//-------------------------------计算原图中心点的方向梯度直方图---------------------
//声明一个直方图数组
Mat
originHist
=
Mat
::
zeros
(
bins_count
,
1
,
CV_32FC1
);
float
*
oh
=
(
float
*
)
originHist
.
data
;
if
(
!
originHist
.
isContinuous
())
{
cout
<<
"直方图地址存储不连续"
<<
endl
;
getchar
();
}
calcOrientationHist
(
grayImage
,
center
,
radius
,
oh
,
bins_count
,
isSmoothed
,
isWeighted
,
sigma
);
//绘制直方图
string
winname
=
"Origin hist"
;
DrawHist
(
originHist
,
winname
);
//---------------计算旋转图像的方向梯度直方图-------------------------------------------
//step:1 计算绕图像中点顺时针旋转30度缩放因子为1的旋转矩阵
Point
rot_center
=
center
;
//旋转中心
double
angle
=
30.0
;
//旋转角度
double
scale
=
1.
;
//缩放因子
/// 通过上面的旋转细节信息求得旋转矩阵
Mat
rot_mat
=
getRotationMatrix2D
(
rot_center
,
angle
,
scale
);
cout
<<
"旋转矩阵:"
<<
rot_mat
<<
endl
;
/// 调用仿射变换函数旋转原始图像
Mat
rotate_dst
;
warpAffine
(
grayImage
,
rotate_dst
,
rot_mat
,
grayImage
.
size
()
);
//声明一个直方图数组
Mat_
<
float
>
rotateHist
=
Mat
::
zeros
(
bins_count
,
1
,
CV_32FC1
);
float
*
rh
=
(
float
*
)
rotateHist
.
data
;
calcOrientationHist
(
rotate_dst
,
center
,
radius
,
rh
,
bins_count
,
isSmoothed
,
isWeighted
,
sigma
);
//绘制直方图
string
winname2
=
"rotated hist"
;
DrawHist
(
rotateHist
,
winname2
);
//- -利用旋转前和旋转后的两个直方图的纵轴主峰对应的角度bin估算图像的旋转角度--------------------
cout
<<
"直方图bin的宽度: "
<<
(
360.f
/
bins_count
)
<<
"度"
<<
endl
;
//求出旋转前图像方向梯度直方图的主峰位置对应的bin角度值
Point
max_location1
;
//直方图主峰对应的bin位置
float
angle1
;
minMaxLoc
(
originHist
,
0
,
0
,
0
,
&
max_location1
);
angle1
=
max_location1
.
y
*
(
360.f
/
bins_count
);
cout
<<
"未旋转之前的方向梯度直方图的主峰位置:"
<<
max_location1
.
y
<<
endl
<<
" ,对应角度值: "
<<
angle1
<<
endl
;;
//求出旋转后图像方向梯度直方图的主峰位置对应的bin角度值
Point
max_location2
;
//直方图主峰对应的bin位置
float
angle2
;
minMaxLoc
(
rotateHist
,
0
,
0
,
0
,
&
max_location2
);
angle2
=
max_location2
.
y
*
(
360.f
/
bins_count
);
cout
<<
"旋转之后的方向梯度直方图的主峰位置:"
<<
max_location2
.
y
<<
endl
<<
" ,对应角度值: "
<<
angle2
<<
endl
;;
cout
<<
"真实旋转角度:"
<<
angle
<<
endl
;
cout
<<
"估计的旋转角度: "
<<
angle2
-
angle1
<<
endl
;
rectangle
(
grayImage
,
StatisticArea
,
Scalar
(
0
),
2
);
imshow
(
"origin img"
,
grayImage
);
rectangle
(
rotate_dst
,
StatisticArea
,
Scalar
(
0
),
2
);
imshow
(
"rotated img"
,
rotate_dst
);
waitKey
(
0
);
return
0
;
}
|
来自CODE的代码片
localorientedgradient.cpp
绕图像中心点顺时针旋转30度缩放因子为1的估计结果:
从上图看出,顺时针旋转奶茶妹妹后,方向梯度直方图整体向左移动了一定距离
真实的旋转角度为 -30度,估计的旋转角度为 -24度,误差6度正好是直方图的bin的宽度
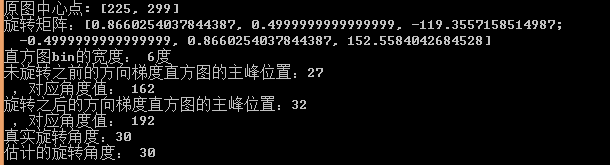
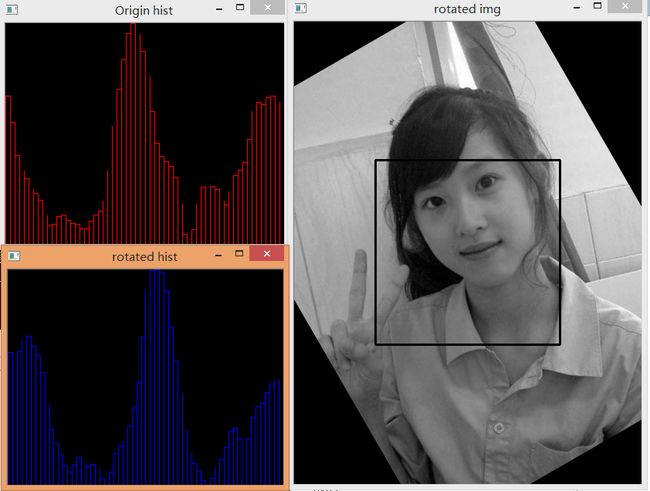
绕图像中心点逆时针旋转30度缩放因子为1的估计结果:
从上图看出,逆时针旋转奶茶妹妹后,方向梯度直方图整体向右移动了一定距离
真实旋转角度为30度,估计的旋转角度也为30度