图之关键路径

今天学习了图的关键路径，来说一说我的心得体会，分享出来，希望帮助到大家。

 在学习之前，我们要先了解一下什么是关键路径，与关键路径相关的知识点是什么。

 关键路径：若有向图中，诸顶点表示事件，诸有向边表示活动持续事件，则该图为活动边网络，简称AOE网。AOE网中的关键路径，就是完成整个网络所需的最短时间，亦最长路径，AOE网中，往往有若干项活动可以平行的进行，因此，从开始顶点到最后一个顶点的最长路径称为关键路径。

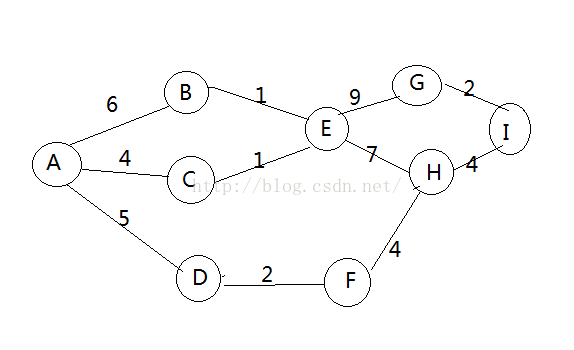
 知识点：1.某事件的最早发生时间：从开始事件到此事件的最长路径，ee表示。比如：ee(E)=max( AB+BE,  AC+CE)=7.只有E事件最早发生时间大于ee(E),才能保证一定完成B,C事件。否则，无法保证。

2.某事件允许的最晚发生时间：比如，el(E)=18-11=7；18为A到I的最长路径，11为E到I的最长路径，这是说保证总的最短时间在18 ，E发生的最早时间是11的情况下，E可以提早，也可以晚会，但最晚是7。

3.缓冲时间，以C为例，最早发生时间是4，允许的最晚发生时间=18-12=6.18为A到I的最长路径,12为C到I的最长路径，6-4=2.说明，C事件可以延时2，这就是缓冲时间。

下边看图：

 

当缓冲时间等于0时，我们叫他关键活动，比如E，ee(E)=7,el(E)=18-11=7,ee(E)=el(E),关键活动连接起来就是关键路径。

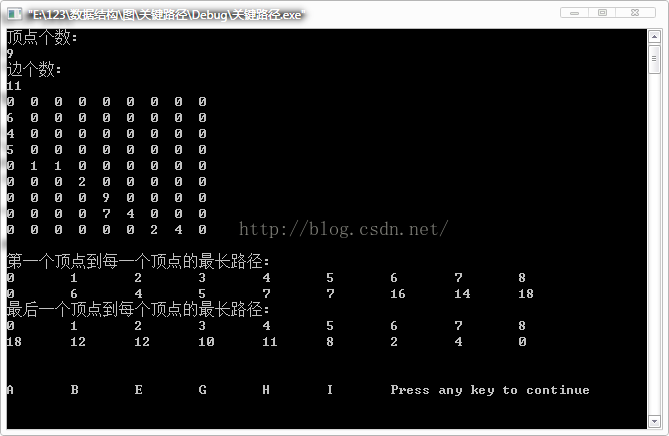
现在我们得到图的邻接矩阵：

我们需要求得就是每个顶点事件的最早发生时间，即最长路径，我们可以通过前一个顶点事件的最长路径加上当前的边的权就是当前事件的最长路径。用，0,1,2,3，。。。分别代表A,B,C,D，，，I

     

  那么我们怎么知道当前事件的前一个顶点事件是否存在呢，通过矩阵，如果不为0,即存在。

通过g->matrix[j][i]+a[j]>max得到，前一个顶点事件的最长路径加上当前的边的权就是当前事件的最长路径。

	int i,j;
	int a[MAX]={0},b[MAX]={-10},c[MAX]={0};
	int max=0;//最长路径
	for( i=0;ivexnum;i++) //列数遍历
	{
		for( j=0;jvexnum;j++)//行数遍历
		{

			if(g->matrix[j][i]>0 && g->matrix[j][i]+a[j]>max) //如果g->matrix[j][i]大于0，说明此顶点有前顶点，由前边的遍历可知，前顶点的最长路径a[j]，
															  //加上g->matrix[j][i]的路径就是当前a[i]的路径
			{
				max=g->matrix[j][i]+a[j];
				a[i]=max;
			}
		}
		max=0;
	}

求出第一个顶点到每一个顶点的最长路径后，我们要求出每一个顶点事件到终点的发生时间。把矩阵转个向即可得出：

  这是代码：

	for( i=g->vexnum-1;i>=0;i--) //列数遍历
		{
			for( j=g->vexnum-1;j>=0;j--)//行数遍历
			{

				if(g->matrix[i][j]>0 && g->matrix[i][j]+b[j]>max) //如果g->matrix[j][i]大于0，说明此顶点有前顶点，由前边的遍历可知，前顶点的最长路径a[j]，
																  //加上g->matrix[j][i]的路径就是当前a[i]的路径
				{
					max=g->matrix[i][j]+b[j];
					b[i]=max;
				}
			}
			max=0;
		}

最后，相比较就行了。

        源代码：

#include
#include
#include 
#include 
#define MAX 20
#define INF 100      // 此处修改最大值
#define nLENGTH(a)  (sizeof(a)/sizeof(a[0]))
#define eLENGTH(a) ( sizeof(a) / sizeof(char) )/ ( sizeof(a[0]) / sizeof(char) )
typedef struct _graph
{
    char vexs[MAX];       // 顶点集合
    int vexnum;           // 顶点数
    int edgnum;           // 边数
    int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;
// 边的结构体 
typedef struct _EdgeData
{
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重
}EData;
//指向节点的位置
int point_node(PGraph g,char c)
{
	for(int i=0;ivexnum;i++)
	{
		if(g->vexs[i]==c)
		{
			return i;
		}
	}
	return -1;
}
PGraph create_graph(int b[][3],char a[],int n,int e)
{
	char c1,c2; //边的2个顶点
	PGraph g; //矩阵
	g=(PGraph)malloc(sizeof(Graph));
	//memset()第一个参数 是地址，第二个参数是开辟空间的初始值，第三个参数是开辟空间的大小
	memset(g, 0, sizeof(Graph));
	printf("顶点个数:\n");//顶点数
	g->vexnum=n;
	printf("%d\n",g->vexnum);
	printf("边个数:\n");//边数
	g->edgnum=e;
	printf("%d\n",g->edgnum);
	//初始化顶点
	for(int j=0;jvexnum;j++)
	{
		g->vexs[j]=a[j];
	}
	for(int i=0;iedgnum;i++)
	{
		int p1,p2;
		c1=char(b[i][0]);
		c2=char(b[i][1]);
		p1=point_node(g, c1);
		p2=point_node(g, c2);
		if (p1==-1 || p2==-1)
        {
            printf("input error: invalid edge!\n");
            free(g);
            continue;
        }
		g->matrix[p1][p2]=b[i][2];
		
	}
	return g;
}

//关键路径的最短时间
//关键路径法（Critical Path Method，CPM）
void CPM_road(PGraph g)
{
	int i,j;
	int a[MAX]={0},b[MAX]={-10},c[MAX]={0};
	int max=0;//最长路径
	for( i=0;ivexnum;i++) //列数遍历
	{
		for( j=0;jvexnum;j++)//行数遍历
		{

			if(g->matrix[j][i]>0 && g->matrix[j][i]+a[j]>max) //如果g->matrix[j][i]大于0，说明此顶点有前顶点，由前边的遍历可知，前顶点的最长路径a[j]，
															  //加上g->matrix[j][i]的路径就是当前a[i]的路径
			{
				max=g->matrix[j][i]+a[j];
				a[i]=max;
			}
		}
		max=0;
	}
	//显示最长路径
	printf("第一个顶点到每一个顶点的最长路径:");
	printf("\n");
	for(i=0;ivexnum;i++) 
	{
		printf("%d\t",i);
	}
	printf("\n");
	for(i=0;ivexnum;i++) 
	{
		printf("%d\t",a[i]);
	}
	printf("\n");
	printf("最后一个顶点到每个顶点的最长路径:");
		for( i=g->vexnum-1;i>=0;i--) //列数遍历
		{
			for( j=g->vexnum-1;j>=0;j--)//行数遍历
			{

				if(g->matrix[i][j]>0 && g->matrix[i][j]+b[j]>max) //如果g->matrix[j][i]大于0，说明此顶点有前顶点，由前边的遍历可知，前顶点的最长路径a[j]，
																  //加上g->matrix[j][i]的路径就是当前a[i]的路径
				{
					max=g->matrix[i][j]+b[j];
					b[i]=max;
				}
			}
			max=0;
		}

	//显示最长路径
	printf("\n");
	for(i=0;ivexnum;i++) 
	{
		printf("%d\t",i);
	}
	printf("\n");
	for(i=0;ivexnum;i++) 
	{
		printf("%d\t",b[i]);
	}
	printf("\n");
	for(i=0;ivexnum;i++)
	{
		if(a[i]==a[g->vexnum-1]-b[i])
		{
				printf("%c\t",g->vexs[i]);
		}
	}



}




//测试
int main()
{
	int i,j;
	PGraph gp;
	//测试用例


	char a[]={'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I'};
	int b[][3]={
        {'A', 'B',6}, 
        {'A', 'C',4}, 
        {'A', 'D',5}, 
        {'B', 'E',1}, 
        {'C', 'E',1}, 
        {'D', 'F',2}, 
        {'E', 'G',9},
		{'E', 'H',7},
		{'F', 'H',4},
		{'G', 'I',2},
		{'H', 'I',4}}; 

	//测试用例

	int n=nLENGTH(a);
	int e=eLENGTH(b);
	gp=create_graph(b,a,n,e);

	//打印矩阵
	for (i = 0; i < gp->vexnum; i++)
    {
        for (j = 0; j < gp->vexnum; j++)
            printf("%d  ", gp->matrix[j][i]);
        printf("\n");
    }
	printf("\n");
	CPM_road(gp);
	return 0;

}