栈(顺序栈，链栈，共享栈）总结

栈是线性表，其特殊性在于有特殊的运算规则。即：栈结构只能在一端进行操作，该操作端称为栈顶，另一端称为栈底。

栈的特性：

1.只能在一端进行操作

2.按照“后进先出”原则处理数据节点。

目录

 1. 顺序栈

顺序栈的定义

顺序栈的初始化

判断栈空(栈底等于栈顶即为空)

顺序栈的入栈

顺序栈的出栈

取栈顶元素

求顺序栈的长度 

 

2.链栈

链栈的定义

初始化一个栈 

 判空

 入栈

 出栈

取出栈顶元素 

求链栈的长度

3.共享存储空间的顺序栈

定义

初始化

求共享栈长度

 入栈

出栈

取栈顶元素操作

---

 1. 顺序栈

顺序栈是利用顺序存储结构实现的栈，即利用一组地址连续的存储单元依次存放自栈底到栈顶的元素数据。分别使用top指针和base指针指向栈顶和栈底。

• 栈为空的标志是：top==base.
• 要注意的是：非空栈的栈顶指针 top 总是指向栈顶元素的上一个位置。

首先，因为该顺序栈要实现扩容，则不能用数组来实现。因此可以动态申请一块内存，将栈中元素放入其中。通过动态内存申请返回的指针来以数组的形式访问栈中元素,其次该动态内存的大小初始时可以设置为已默认值，如果超过默认值时，可以重新申请更大的内存，从而达到扩容的目的。

• 顺序栈的定义

#define StackInitsize 100 //顺序栈的初始大小
#define StackIncrement 10 //顺序栈的储存空间增量
#define ElemType BiTree
typedef struct
{
    ElemType *base;        	 	// 顺序栈的储存空间基地址
    int top;          		// 栈顶指针
    int stacksize;          // 栈容量
}SqStack;

• 顺序栈的初始化

void InitStack(SqStack &S)				// 栈的初始化
{
    S.base=(ElemType*)malloc(sizeof(ElemType*));
    if(!S.base)
        return;
    S.top=0;//栈顶指针初值为0
    S.stacksize=StackInitsize;//当前空间大小为初始值StackInitSize
}
/*
void InitStack(SqStack &S)
{
    S.base=new ElemType[StackInitSize];
    S.top=0;
    S.stacksize=StackInitSize;
}
*/

• 判断栈空(栈底等于栈顶即为空)

int StackEmpty(SqStack S)
{
    if(S.top==0)
        return 1;
    else
        return 0;
//为空返回1！
}
/*
bool StackEmpty(SqStack S)
{
    return S.top?false:true;
}
*/

• 顺序栈的入栈

void Push(SqStack &S,ElemType e)
{
    if(S.top>=S.stacksize)//栈已满，需扩充
    {
        S.base=(ElemType*)realloc(S.base,(S.stacksize+StackIncrement)*sizeof(ElemType));
        if(!S.base)
            return;
        S.stacksize+=StackIncrement;
    }
    S.base[S.top++]=e;//插入元素e后，栈顶再指针加1！
}

• 顺序栈的出栈

void Pop(SqStack &S,ElemType &e)
{
    if(S.top==0)
        return;
    e=S.base[--S.top];//栈顶指针-1，出栈元素给e
}

• 取栈顶元素

int GetTop(SqStack S,ElemType &e)

{
    if(S.top==0)
        return 0;
    e=S.base[S.top-1];//栈顶指针不变，取出栈顶元素给e
     return 1;
}

• 求顺栈的长度 

int StackLength(SqStack S)
{
    return S.top;
}

 

2.链栈

链式栈是由单链表来实现的，所以与单链表的结点结构相同。由数据域和指向下一个结点的next域组成。

注意链栈next指针的指向，与队列不同： 
如果插入一个元素，栈末尾的next指针是指向前一个已经在栈中的元素的 
而队列则是，插入一个元素，其next指针是往外指，指向空。 
链栈的next指针之所以这样，是方便删除操作 

• 链栈的定义

 ///定义链栈
typedef struct LNode
{
    ElemType data;
    struct LNode *next;
}LNode,*Linklist;
/*
typedef struct LNode
{
    ElemType data;
    struct LNode *next;
    LNode (int Data=0,struct LNode * Next=NULL)
    {
        data=Data;
        next=Next;
    }
}LNode ,*LinkList ;
*/

• 初始化一个栈 

///初始化一个栈
void InitStack(Linklist &LS)
{
    LS=NULL;
}

•  判空

///判空
int StackEmpty(Linklist LS)
{
    ///若栈位空则返回真，否则返回假
    if(LS==NULL)
        return 1;
    return 0;
}
/*
bool StackEmpty(LinkList LS)
{
    return LS?false:true;
}
*/

•  入栈

///入栈
void Push(Linklist &LS,ElemType e)
{
    ///使定义的元素bt进栈，使其成为新的栈顶元素
    Linklist s;
    s=(Linklist)malloc(sizeof(LNode));
    s->data=e;
    s->next=LS;///插入节点
    LS=s;///修改头指针（很重要！）
}
/*
void Push(LinkList &LS,ElemType e)
{
    LinkList s;
    s=new LNode(e,LS);//注意这里！
    LS=s;
}
*/

•  出栈

///出栈
void Pop(Linklist &LS,ElemType &e)
{
    ///若栈非空，取出栈顶元素，并用bt返回其值
    if(LS==NULL)
        return;
    Linklist s;
    e=LS->data;
    s=LS;
    LS=LS->next;
    free(s);///释放节点
}

• 取出栈顶元素 

///取出栈顶元素
int GetTop(Linklist &LS,ElemType &e)
{
    if(LS==NULL)
        return 0;
    e=LS->data;
    return 1;
}

• 求链栈的长度

//3、求链栈的长度StackLength
int StackLength(LinkList LS)
{
    int cnt=0;
    LinkList p=LS;
    while(p){
        cnt++;p=p->next;
    }
    return cnt;
}

 

3.共享存储空间的顺序栈

根据书上描述，共享栈的特点是：两个栈顶，置放在数组两头，入栈迎面相向，相遇时栈满，看图示：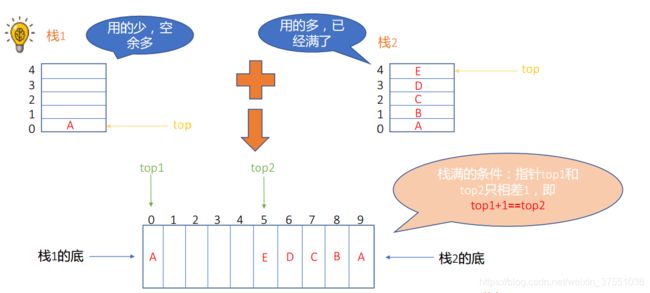

主要处理三步工作：
第一，栈空的标志。这里沿用前面的约定，左栈top1=0，而右栈用top2=MAXSIZE-1，也就是放在数组的最左右两端。
第二，判满。这里采用左栈+1=右栈表明栈满。

第三，还需要一个状态标志flag(i=1，i=2)，让用户选择是哪一个栈进行操作。

• 定义

typedef struct
{
    ElemType data[StackSize];
    int top1,top2;
}DuSqStack;

 

• 初始化

void InitStack(DuSqStack &S)
{
    S.top1=0,S.top2=StackSize-1;
}

 

• 求长度

int StackLength(DuSqStack S,int i)
{

    int flag=i%2;
    return flag?S.top1:StackSize-S.top2-1;
}

•  入栈

void Push(DuSqStack &S,int i,ElemType e)
{
    if(S.top1-S.top2==1)
    {
        printf("error !!! Stack is full\n");
        return ;
    }
     S.data[(i&1?S.top1++:S.top2--)]=e;
}

• 出栈

void Pop(DuSqStack &S,int i,ElemType &e)
{
    if(i==1)
    {
        if(S.top1==0)
        {
            printf("error !!! Stack1 is empty\n");
            return ;
        }
        e=S.data[--S.top1];
    }
    else
    {
        if(S.top2==StackSize-1)
        {
            printf("error !!! Stack2 is empty\n");
        }
        e=S.data[++S.top2];
    }
}

•  取栈顶元素操作

void GetTop(DuSqStack S,int i,ElemType &e)
{
    if(i==1)
    {
        if(S.top1==0)
        {
            printf("error !!! Stack1 is empty\n");
            return ;
        }
        e=S.data[S.top1-1];
    }
    else
    {
        if(S.top2==StackSize-1)
        {
            printf("error !!! Stack2 is empty\n");
        }
        e=S.data[S.top2+1];
    }
}