自动控制原理学习笔记(五)
第五章 线性系统频域分析法
5.1 频率特性 G ( j ω ) G(j\omega) G(jω)基本概念
-
频率响应:线性系统稳态正弦响应的幅值、相角随输入频率变化的规律。
ω \omega ω 从0到 + ∞ +\infty +∞ 变化时, G ( j ω ) G(j\omega) G(jω) 幅值和相位随 ω \omega ω 的变化。
-
仅适用于线性定常系统。
-
给系统一个脉冲信号 δ ( t ) \delta(t) δ(t), 得到脉冲响应 k ( t ) k(t) k(t) ,对脉冲响应做傅里叶变换即得到频率特性 G ( j ω ) G(j\omega) G(jω)。
-
是系统的固有属性,由系统的结构和参数决定。
-
不稳定的系统观察不到频率特性。
-
计算器可以求复数的幅值和相角(考前复习)
-
一般讨论仅针对 ω ∈ [ 0 , + ∞ ) \omega \in [0,+\infty) ω∈[0,+∞),若涉及到 ω < 0 \omega < 0 ω<0
则有
{ ∣ G ( j ω ) ∣ = ∣ G ( − j ω ) ∣ ∠ G ( j ω ) = − ∠ G ( j ω ) 或 { R e [ G ( j ω ) ] = R e [ G ( − j ω ) ] I m [ G ( j ω ) ] = − I m [ − G ( j ω ) ] \begin{cases} |G(j\omega)|=|G(-j\omega)|\\ \angle G(j\omega)=-\angle G(j\omega)\\ \end{cases}\\ 或\\ \begin{cases} Re[G(j\omega)]=Re[G(-j\omega)]\\ Im[G(j\omega)]=-Im[-G(j\omega)]\\ \end{cases} {∣G(jω)∣=∣G(−jω)∣∠G(jω)=−∠G(jω)或{Re[G(jω)]=Re[G(−jω)]Im[G(jω)]=−Im[−G(jω)]
频率特性 G ( j ω ) G(j\omega) G(jω)定义(三种)
- 定义一:幅值比,相位差(求频率特性的实验方法)
G ( j ω ) = ∣ G ( j ω ) ∣ ∠ G ( j ω ) G(j\omega)=|G(j\omega)|\angle G(j\omega) G(jω)=∣G(jω)∣∠G(jω)
其中
∣ G ( j ω ) ∣ = ∣ C s ( t ) ∣ ∣ r ( t ) ∣ 输 出 和 输 入 的 幅 值 比 ∠ G ( j ω ) = ∠ C s ( t ) − ∠ r ( t ) 输 出 和 输 入 的 相 位 差 |G(j\omega)|=\dfrac{|C_s(t)|}{|r(t)|} 输出和输入的幅值比\\ \angle G(j\omega)=\angle C_s(t)-\angle r(t) 输出和输入的相位差 ∣G(jω)∣=∣r(t)∣∣Cs(t)∣输出和输入的幅值比∠G(jω)=∠Cs(t)−∠r(t)输出和输入的相位差
- 定义二:直接用 j ω j\omega jω 替代闭环传递函数中的s
G ( j ω ) = G ( s ) ∣ s = j ω G(j\omega)=G(s)|_{s=j\omega} G(jω)=G(s)∣s=jω
-
定义三:输出信号与输入信号的傅里叶变换之比
对比傅里叶变换和拉氏变换的定义
G ( j ω ) = F [ G ( t ) ] = ∫ − ∞ + ∞ g ( t ) e − j ω t d t G ( s ) = L [ G ( t ) ] = ∫ − ∞ + ∞ g ( t ) e − s t d t G(j\omega)=F[G(t)]=\int_{-\infty}^{+\infty}g(t)e^{-j\omega t}dt\\ G(s)=L[G(t)]=\int_{-\infty}^{+\infty}g(t)e^{-st}dt G(jω)=F[G(t)]=∫−∞+∞g(t)e−jωtdtG(s)=L[G(t)]=∫−∞+∞g(t)e−stdt
最小相位与非最小相位环节
- 定义:在幅频特性相同的系统中,相频变化最小的系统称为最小相位系统。
- 结论:最小相位系统没有右半复平面的零极点(所有零极点都小于或等于零),也无延迟环节。是稳定的。非最小相位系统有一个或多个右半复平面的零极点。
- 事实:两个不同的传递函数可以有相同的幅频特性,其中相频特性变化范围小的那个是最小相位系统。
- 最小相位 ⟺ \iff ⟺ Lyapunov意义的稳定(包括等幅振荡)。
做题注意
要判断 G ( j ω ) G(j\omega) G(jω) 实部和虚部的正负号,来判断所在的象限,从而判断相角的范围。
5.2 频率特性几何表示法(三种)
1. Nyquist图(八大典型环节)
定义:将频率特性 G ( j ω ) G(j\omega) G(jω)写成模和幅角的形式,角频率 ω \omega ω 从0 到 + ∞ +\infty +∞ ,将 G ( j ω ) G(j\omega) G(jω) 的轨迹画在复平面中。
特点:某一频率特性 G ( j ω ) G(j\omega) G(jω) 乘某一常数K, 原曲线各点的幅值扩大为K倍,相角不变。
若要画 0 → − ∞ 0\rightarrow -\infty 0→−∞ 的Nyquist图,则与 0 → + ∞ 0 \rightarrow +\infty 0→+∞ 的曲线关于实轴对称即可。
- 惯性环节 K 1 + T s \dfrac{K}{1+Ts} 1+TsK 的Nyquist图是半圆,证明:
-
(5)一阶微分: G ( s ) = 1 + T s G(s)=1+Ts G(s)=1+Ts
∣ G ( j ω ) ∣ = 1 + ( T ω ) 2 ∠ G ( j ω ) = a r c t a n ( T ω ) |G(j\omega)|=\sqrt{1+(T\omega)^2}\\ \angle G(j\omega)=arctan(T\omega) ∣G(jω)∣=1+(Tω)2∠G(jω)=arctan(Tω)
-
(6)二阶震荡环节
产生谐振峰值的条件: 0 < ξ < 0.707 0<\xi<0.707 0<ξ<0.707
谐 振 频 率 ω r = ω n 1 − 2 ξ 2 谐 振 峰 值 M r = ∣ G ( j ω r ) ∣ = 1 2 ξ 1 − ξ 2 谐振频率 \omega_r=\omega_n\sqrt{1-2\xi^2}\\ 谐振峰值 M_r=|G(j\omega_r)|=\dfrac{1}{2\xi\sqrt{1-\xi^2}} 谐振频率ωr=ωn1−2ξ2谐振峰值Mr=∣G(jωr)∣=2ξ1−ξ21
二阶震荡环节的转折点、谐振频率、谐振峰值
转折点 ω = ω n \omega=\omega_n ω=ωn 对应的相角为-90°
-
(7)二阶微分
-
(8)延迟环节
典型环节的组合(连乘积)
- 多个环节相乘,幅值相乘,相角相加。
- 多个环节相除,幅值相除,相角相减。
- 开环传函才能写成多个典型环节的连乘积。
系统的开环幅相频率特性画法
着重求起点和终点,必要时求出与实轴、虚轴的交点。
-
起点: ω = 0 \omega=0 ω=0 时,除放大环节幅值为K, 积分环节相角为-90°,其余环节均幅值为1,相角为0。系统有 v v v 个积分环节串联时,开环Nyquist图从 $ \omega=0^+ $ 开始,起点处相角为 − v ⋅ 90 ° -v\cdot90° −v⋅90°,
故起点
{ K ∠ 0 ° , v = 0 ∞ ∠ − 90 ° ⋅ v , v ≥ 1 \begin{cases} K\angle 0°,v=0\\ \infty \angle -90°\cdot v,v \ge 1 \end{cases} {K∠0°,v=0∞∠−90°⋅v,v≥1
-
终点:当 ω → ∞ \omega \rightarrow \infty ω→∞ ,每个惯性环节、积分环节、振荡环节曲线的切线方向为其阶数乘(-90°);每个微分环节曲线切线方向为其阶数乘(+90°),所以 ω → ∞ \omega \rightarrow \infty ω→∞ 时开环Nyquist图中曲线切线方向是**(n-m)(-90°)**,n为分母的阶数,m为分子的阶数。
0 ∠ − 90 ° ( n − m ) 0\angle-90°(n-m) 0∠−90°(n−m)
2. Bode图(对数幅频特性)
- 横坐标为 l g ω lg\omega lgω,横轴上两点的距离也为 l g ω 2 − l g ω 1 lg\omega_2-lg\omega_1 lgω2−lgω1。
- 原特性乘以K,幅频特性曲线图上平移 20 l g K 20lgK 20lgK 个单位
幅 频 特 性 , 单 位 d B L ( ω ) = 20 l g ∣ G ( j ω ) ∣ 相 频 特 性 , 单 位 为 ° φ ( ω ) = ∠ G ( j ω ) 幅频特性,单位dB\\ L(\omega)=20lg|G(j\omega)|\\ 相频特性,单位为°\\ \varphi(\omega)=\angle G(j\omega) 幅频特性,单位dBL(ω)=20lg∣G(jω)∣相频特性,单位为°φ(ω)=∠G(jω)
惯性环节Bode图(转折频率的概念)

振荡环节Bode图
振荡环节转折频率为 ω n \omega_n ωn
阻尼比越小,相频特性在 ω = ω n \omega=\omega_n ω=ωn 附近越陡。

- 振荡环节渐近幅频特性修正表
| ξ \xi ξ | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 1.2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 修正值 dB | +20 | +14 | +10.5 | +8 | +6 | +4.4 | +1.94 | 0 | -1.6 | -2.92 | -4 | -6 |
典型环节的Bode图
剪切频率
L ( ω ) L(\omega) L(ω) 与横轴的交点,对应的 ω \omega ω 值记为 ω c \omega_c ωc , 有 ∣ G ( j ω c ) ∣ = 1 , L ( ω c ) = 0 |G(j\omega_c)|=1, L(\omega_c)=0 ∣G(jωc)∣=1,L(ωc)=0 。
绘制系统的开环Bode图的步骤
- 将频率特性化为标准形式(尾1)
- 顺序列出转折频率
- 确定基准线
- 叠加作图
- 修正
- 检查
对数幅频特性的每一个转折点,都对应相频特性的一个连续、光滑、渐变的过渡,自左向右相角变化的增量为
| 环节 | 相角增量 | 幅值增量 |
|---|---|---|
| 惯性环节 | -90° | -20dB/dec |
| 一阶微分 | +90° | +20dB/dec |
| 震荡环节 | -180° | -40dB/dec |
| 二阶微分 | +180° | +40dB/dec |
关于基准点/线(用于确定最左边的图形)
在幅频特性的最左边,级最低频段,只有放大环节和积分环节的对数幅频特性不为零,**故该段的幅频特性取决于 K s v \dfrac{K}{s^v} svK,**当 v > 0 v>0 v>0,可确定该最低频段的斜率是 − 20 ⋅ v ( d B / d e c ) -20\cdot v (dB/dec) −20⋅v(dB/dec), 且延长线必过 ω = 1 , L ( ω ) = 20 l g K \omega=1,L(\omega)=20lgK ω=1,L(ω)=20lgK 这点,可确定与纵轴的交点。
若 v = 0 v=0 v=0, 则斜率为0。则与纵轴交点为 20 l g K 20lgK 20lgK。
振荡环节修正值:在转折频率处为 20 l g 1 2 ξ 20lg\dfrac{1}{2\xi} 20lg2ξ1,在峰值频率处为 20 l g 1 2 ξ 1 − ξ 2 20lg\dfrac{1}{2\xi\sqrt{1-\xi^2}} 20lg2ξ1−ξ21 (课后题5-8,5-10)
振荡环节渐近幅频特性修正表
| ξ \xi ξ | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 1.2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 修正值 dB | +20 | +14 | +10.5 | +8 | +6 | +4.4 | +1.94 | 0 | -1.6 | -2.92 | -4 | -6 |
5.3 闭环系统稳定性分析
闭环系统稳定的充要条件:
- 闭环特征方程 D ( s ) = 0 D(s)=0 D(s)=0的n个根全部具有负实部。
- 当 ω \omega ω 从 0 → + ∞ , D ( j ω ) 0 \rightarrow +\infty, D(j\omega) 0→+∞,D(jω) 的相角增量为 n π 2 n\dfrac{\pi}{2} n2π 。(推导书P232)
辅助函数F(s)
系统的开环传函设为 G ( s ) H ( s ) = K M ( s ) N ( s ) G(s)H(s)=\dfrac{KM(s)}{N(s)} G(s)H(s)=N(s)KM(s) ,分母阶数为n,分母阶数为m。常有n>m
闭环系统特征方程 D ( s ) = K M ( s ) + N ( s ) = 0 D(s)=KM(s)+N(s)=0 D(s)=KM(s)+N(s)=0
引入辅助函数 F ( s ) = 1 + G ( s ) H ( s ) = D ( s ) N ( s ) F(s)=1+G(s)H(s)=\dfrac{D(s)}{N(s)} F(s)=1+G(s)H(s)=N(s)D(s), 分子分母阶数均为n
结论一(开环稳定时闭环稳定的条件)
若系统开环极点全部在左半平面,则闭环系统稳定的充要条件是:
ω = 0 → + ∞ \omega=0\rightarrow+\infty ω=0→+∞, F ( s ) F(s) F(s) 的相角变化量为0。
结论二(开环不稳定时闭环稳定的条件)
若系统的n个开环极点中有P个在右半平面,剩下n-P个在左半平面,则闭环稳定的充要条件是:
ω = 0 → + ∞ \omega=0\rightarrow+\infty ω=0→+∞, F ( s ) F(s) F(s) 的相角变化量为P π \pi π。
结论三(开环传函有串联积分环节)
G ( s ) H ( s ) = K M ( s ) s v N ′ ( s ) G(s)H(s)=\dfrac{KM(s)}{s^vN'(s)} G(s)H(s)=svN′(s)KM(s)
把 j ω j\omega jω 修改沿虚轴变化的路线在原点处做一修改
若系统的n个开环极点中有 v v v 个位于原点,P个在右半平面,剩下n-P个在左半平面,则闭环稳定的充要条件是:
ω = ( 0 + , j 0 ) → ( 0 , j 0 + ) → ( 0 , j ∞ ) \omega=(0^+,j0)\rightarrow(0,j0^+)\rightarrow(0,j\infty) ω=(0+,j0)→(0,j0+)→(0,j∞), F ( s ) F(s) F(s) 的相角变化量为P π \pi π。
Nyquist判据(由开环频率特性判断闭环稳定性)
-
若开环无串联积分环节,则闭环稳定 ⟺ \iff ⟺ G ( s ) H ( s ) G(s)H(s) G(s)H(s)的Nyquist曲线绕点 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点逆时针转过 P π P\pi Pπ
-
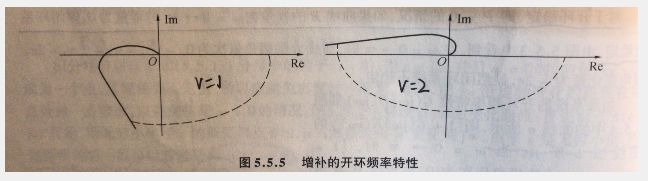
若开环有串联积分环节,则闭环稳定 ⟺ \iff ⟺ G ( s ) H ( s ) G(s)H(s) G(s)H(s)的增补Nyquist曲线绕点 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点逆时针转过 P π P\pi Pπ
增补方法:在实轴正或负(具体取决于 ω = 0 \omega=0 ω=0时G(j0)是正数还是负数)半轴无穷远处,以原点为圆心, ∞ \infty ∞为半径逆时针画过 v π 2 v\dfrac{\pi}{2} v2π,与 ω \omega ω从 0 + 0^+ 0+开始的Nyquist图连接起来 。
- 由于常常为单位负反馈,可直接画 G ( j ω ) G(j\omega) G(jω) 的Nyquist图来判断。
易错题
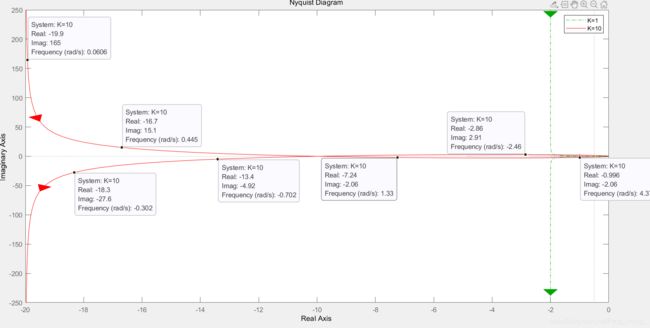
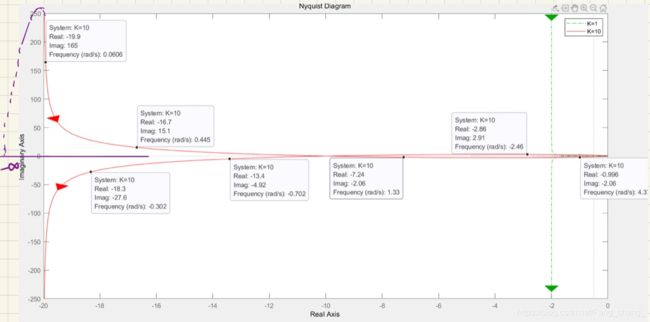
开环传函 G ( s ) = 10 ( s + 1 ) s ( s − 1 ) G(s)=\dfrac{10(s+1)}{s(s-1)} G(s)=s(s−1)10(s+1),Matlab求出的Nyquist图如下,试判断单位负反馈闭环系统稳定性。
Solution:Matlab画出的是全频段 ω = − ∞ → 0 → + ∞ \omega=-\infty \rightarrow 0\rightarrow +\infty ω=−∞→0→+∞,我们只研究正半部分。由于有串联一个积分环节,故需要画出增补的Nyquist图。如下
围绕 ( − 1 , j 0 ) (-1,j0) (−1,j0)绕过的角度恰为 P π , P = 1 P\pi,P=1 Pπ,P=1,系统稳定。