卡尔曼滤波及例程

1、五大公式

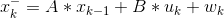   预测状态

          预测协方差

   kalman增益

  状态估计值

           当前状态方差

其中：

          为测量值，为测量噪声，

:预测值         A:状态转移矩阵          :状态的控制量       :过程造噪声，假定其符合均值为0,协方差矩阵为Q的多元正太分布，

H:测量矩阵，从真实值到测量值的状态转移矩阵

2、python demo

# -*- coding=utf-8 -*-
# Kalman filter example demo in Python
 
# A Python implementation of the example given in pages 11-15 of "An
# Introduction to the Kalman Filter" by Greg Welch and Gary Bishop,
# University of North Carolina at Chapel Hill, Department of Computer
# Science, TR 95-041,
# http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html
 
# by Andrew D. Straw
#coding:utf-8
import numpy
import pylab
 
#这里是假设A=1，H=1的情况
 
# intial parameters
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # truth value (typo in example at top of p. 13 calls this z)
z = numpy.random.normal(x,0.1,size=sz) # observations (normal about x, sigma=0.1)
 
Q = 1e-5 # process variance
 
# allocate space for arrays
xhat=numpy.zeros(sz)      # a posteri estimate of x
P=numpy.zeros(sz)         # a posteri error estimate
xhatminus=numpy.zeros(sz) # a priori estimate of x
Pminus=numpy.zeros(sz)    # a priori error estimate
K=numpy.zeros(sz)         # gain or blending factor
 
R = 0.1**2 # estimate of measurement variance, change to see effect
 
# intial guesses
xhat[0] = 0.0
P[0] = 1.0
 
for k in range(1,n_iter):
    # time update
    xhatminus[k] = xhat[k-1]  #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
    Pminus[k] = P[k-1]+Q      #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
 
    # measurement update
    K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
    xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
    P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
 
pylab.figure()
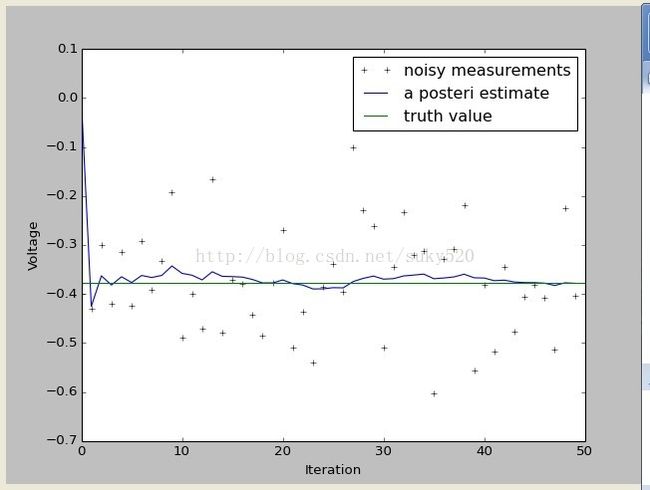
pylab.plot(z,'k+',label='noisy measurements')     #测量值
pylab.plot(xhat,'b-',label='a posteri estimate')  #过滤后的值
pylab.axhline(x,color='g',label='truth value')    #系统值
pylab.legend()
pylab.xlabel('Iteration')
pylab.ylabel('Voltage')
 
pylab.figure()
valid_iter = range(1,n_iter) # Pminus not valid at step 0
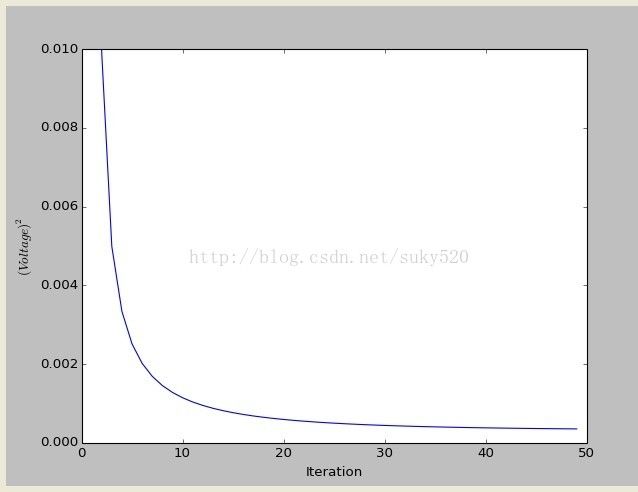
pylab.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
pylab.xlabel('Iteration')
pylab.ylabel('$(Voltage)^2$')
pylab.setp(pylab.gca(),'ylim',[0,.01])
pylab.show()

3、鼠标跟踪

#include 
#include 

#include 
using namespace Ros_node;
using namespace cv;
using namespace std;

const int winWidth = 800;
const int winHeight = 600;

Point mousePosition = Point(winWidth>>1, winHeight>>1);

//mouse call back
void mouseEvent(int event, int x, int y, int flags, void *param)
{
  if(event==CV_EVENT_MOUSEMOVE)
  {
    mousePosition=Point(x,y);
  }
}

int main(int argc, char **argv)
{
  ros::init(argc, argv, "ros_node_node");
  //1.kalman filter setup
  const int stateNum=4;
  const int measureNum=2;

  KalmanFilter KF(stateNum, measureNum, 0);
  Mat state (stateNum, 1, CV_32FC1); //state(x,y,detaX,detaY)
  Mat processNoise(stateNum, 1, CV_32F);
  Mat measurement = Mat::zeros(measureNum, 1, CV_32F);	//measurement(x,y)


    randn( state, Scalar::all(0), Scalar::all(0.1) ); //随机生成一个矩阵，期望是0，标准差为0.1;
    KF.transitionMatrix = *(Mat_(4, 4) <<
      1,0,1,0,
      0,1,0,1,
      0,0,1,0,
      0,0,0,1 );//元素导入矩阵，按行;

    //setIdentity: 缩放的单位对角矩阵;
    //!< measurement matrix (H) 观测模型
    setIdentity(KF.measurementMatrix);

    //!< process noise covariance matrix (Q)
    // wk 是过程噪声，并假定其符合均值为零，协方差矩阵为Qk(Q)的多元正态分布;
    setIdentity(KF.processNoiseCov, Scalar::all(1e-5));

    //!< measurement noise covariance matrix (R)
    //vk 是观测噪声，其均值为零，协方差矩阵为Rk,且服从正态分布;
    setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1));

    //!< priori error estimate covariance matrix (P'(k)): P'(k)=A*P(k-1)*At + Q)*/  A代表F: transitionMatrix
    //预测估计协方差矩阵;
    setIdentity(KF.errorCovPost, Scalar::all(1));


    //!< corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
    //initialize post state of kalman filter at random
    randn(KF.statePost, Scalar::all(0), Scalar::all(0.1));
    Mat showImg(winWidth, winHeight,CV_8UC3);

    for(;;)
    {
      setMouseCallback("Kalman", mouseEvent);
      showImg.setTo(0);

      Point statePt = Point( (int)KF.statePost.at(0), (int)KF.statePost.at(1));

      //2.kalman prediction
      Mat prediction = KF.predict();
      Point predictPt = Point( (int)prediction.at(0), (int)prediction.at(1));

      //3.update measurement
      measurement.at(0)= (float)mousePosition.x;
      measurement.at(1) = (float)mousePosition.y;

      //4.update
      KF.correct(measurement);

//      randn( processNoise, Scalar(0), Scalar::all(sqrt(KF.processNoiseCov.at(0, 0))));
//      state = KF.transitionMatrix*state + processNoise;
      //draw
      circle(showImg, statePt, 5, CV_RGB(255,0,0),1);//former point
      circle(showImg, predictPt, 5, CV_RGB(0,255,0),1);//predict point
      circle(showImg, mousePosition, 5, CV_RGB(0,0,255),1);//ture point


// 			CvFont font;//字体
// 			cvInitFont(&font, CV_FONT_HERSHEY_SCRIPT_COMPLEX, 0.5f, 0.5f, 0, 1, 8);
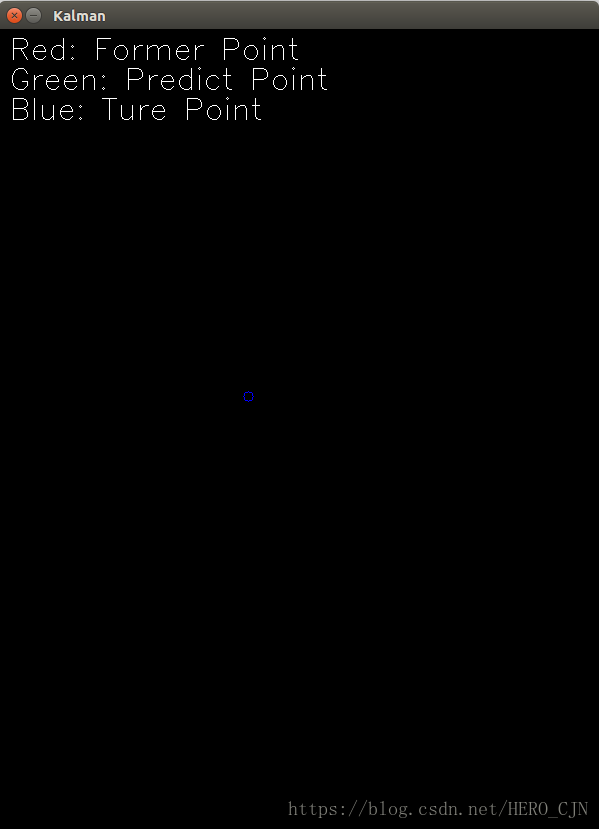
      putText(showImg, "Red: Former Point", cvPoint(10,30), FONT_HERSHEY_SIMPLEX, 1 ,Scalar :: all(255));
      putText(showImg, "Green: Predict Point", cvPoint(10,60), FONT_HERSHEY_SIMPLEX, 1 ,Scalar :: all(255));
      putText(showImg, "Blue: Ture Point", cvPoint(10,90), FONT_HERSHEY_SIMPLEX, 1 ,Scalar :: all(255));

      imshow( "Kalman", showImg );
      int key = waitKey(3);
      if (key == 27)
      {
        break;
      }
    }
}

代码结果显示：

资料：

维基百科 卡尔曼滤波

论文

卡尔曼滤波应用及其matlab实现