BFS 华容道

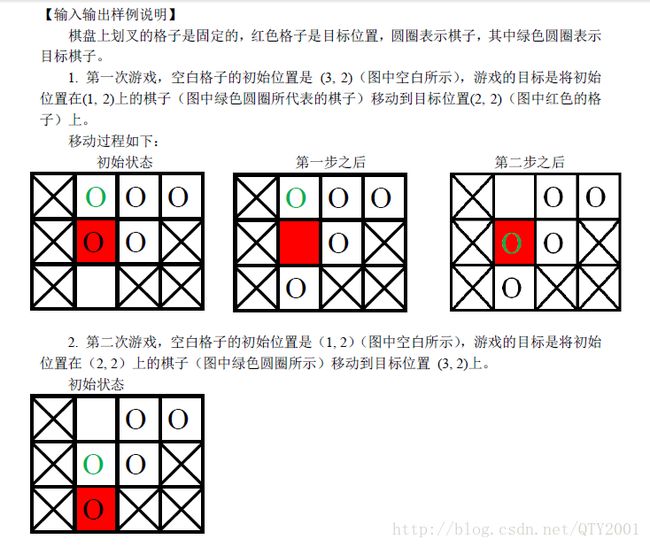
整体思路是BFS没问题，但对于500个询问还是很吃力。但又因为只有一张图，所以我们可以预处理一些东西。
那么来看，对于要移动的点，无非是把空格移动到他的四周，之后交换位置，而交换位置之前有大量无用的转移，而这个转移的耗费对于某个点是确定不变的，而致有转移起点才是有效的，起点与空格交换位置后，空格依然在起点的周围，那么就可以预处理出对于每一个点，他不移动的情况下，若空格在他周围（上下左右）某个位置时，移动到他周围另一个位置的耗费。
而对于主函数，首先处理出空格到起点四周的耗费（因为空格不在起点附近）之后进行spfa，有两个转移。
1，空格从这个点的周围某一位置转移到周围另一个位置，
2，此点与他周围某个位置上的空格交换位置。
细节蛮多的，但推荐自己打。

#include
#include
#include
#include
#include
#include
#define ll long long
#define mod 1000000007
using namespace std;
int n,m,Q,a[35][35],l[35][35][5][5],d[35][35][5],vis[35][35][5];
int v[35][35],dis[35][35],wz[5][2]={0,0,-1,0,0,1,1,0,0,-1},hhh[5],hh[5]={0,3,4,1,2};
struct zb
{
    int x,y;
    zb(){}
    zb(int x_,int y_){x=x_;y=y_;}
}S,T,kg;
struct dp
{
    int x,y,z;
    dp(){}
    dp(int x_,int y_,int z_){x=x_;y=y_;z=z_;}
};
queue q;
queue qq;
void bfs(int x,int y)
{
     memset(dis,30,sizeof(dis));
     dis[x][y]=0;v[x][y]=1;
     q.push(zb(x,y));
     while(!q.empty())
     {
         zb k=q.front();
         for(int i=1;i<=4;i++)
         {
             zb to;to.x=k.x+wz[i][0],to.y=k.y+wz[i][1];
             if(!a[to.x][to.y]||to.x>n||to.x<1||to.y>m||to.y<1)continue;
             if(dis[to.x][to.y]>dis[k.x][k.y]+1)
             {
                  dis[to.x][to.y]=dis[k.x][k.y]+1;
                  if(!v[to.x][to.y])
                  {
                      v[to.x][to.y]=1;
                      q.push(to);
                  }
             }
         }
         q.pop();v[k.x][k.y]=0;
     }
}
void init()
{
     for(int i=1;i<=n;i++)
       for(int j=1;j<=m;j++)
       {
           if(!a[i][j])continue;
           for(int k=1;k<=4;k++)
           {
               a[i][j]=0;
               int x=i+wz[k][0],y=j+wz[k][1];
               //if(x>n||x<1||y>m||y<1)continue;
               bfs(x,y);
               for(int h=1;h<=4;h++)
                  if(h!=k)
                     l[i][j][k][h]=dis[i+wz[h][0]][j+wz[h][1]];
               a[i][j]=1;
           }
       }
}
void spfa()
{
     memset(d,30,sizeof(d));
     for(int i=1;i<=4;i++)
     {
         int x=S.x+wz[i][0],y=S.y+wz[i][1];
         if(!a[x][y]||x<1||x>n||y<1||y>m)continue;
         d[S.x][S.y][i]=hhh[i];vis[S.x][S.y][i]=1;
         qq.push(dp(S.x,S.y,i));
     }
     while(!qq.empty())
     {
          dp k=qq.front();qq.pop();vis[k.x][k.y][k.z]=0;
          int x=k.x+wz[k.z][0],y=k.y+wz[k.z][1];
          if(a[x][y]&&x<=n&&x>=1&&y<=m&&y>=1)
          {
              if(d[x][y][hh[k.z]]>d[k.x][k.y][k.z]+1)
              {
                   d[x][y][hh[k.z]]=d[k.x][k.y][k.z]+1;
                   if(!vis[x][y][hh[k.z]])
                   {
                       vis[x][y][hh[k.z]]=1;
                       qq.push(dp(x,y,hh[k.z]));
                   }
              }
          }
          for(int j=1;j<=4;j++)
          {
              if(j==k.z||!a[k.x+wz[j][0]][k.y+wz[j][1]])continue;
              dp to;to.x=k.x+wz[j][0];to.y=k.y+wz[j][1],to.z=j;
              if(d[k.x][k.y][j]>d[k.x][k.y][k.z]+l[k.x][k.y][k.z][j])
              {
                   d[k.x][k.y][j]=d[k.x][k.y][k.z]+l[k.x][k.y][k.z][j];
                   if(!vis[k.x][k.y][j])
                   {
                       vis[k.x][k.y][j]=1;
                       qq.push(dp(k.x,k.y,j));
                   }
              }
          }
     }
}
int main()
{
    //freopen("PuzzleNOIP2013.in","r",stdin);
    //freopen("PuzzleNOIP2013.out","w",stdout);
    cin>>n>>m>>Q;
    for(int i=1;i<=n;i++)
       for(int j=1;j<=m;j++)
          scanf("%d",&a[i][j]);
    init();
    while(Q--)
    {
        scanf("%d%d%d%d%d%d",&kg.x,&kg.y,&S.x,&S.y,&T.x,&T.y);
        if(S.x==T.x&&S.y==T.y){printf("0\n");continue;}  
        a[S.x][S.y]=0;
        bfs(kg.x,kg.y);
        a[S.x][S.y]=1;
        for(int i=1;i<=4;i++)hhh[i]=dis[S.x+wz[i][0]][S.y+wz[i][1]];
        spfa();
        int ans=100000000;
            for(int i=1;i<=4;i++)ans=min(ans,d[T.x+wz[i][0]][T.y+wz[i][1]][hh[i]]+1);
        if(ans==100000000)printf("-1\n");
        else printf("%d\n",ans);    
    }
}