栈经典问题之前缀、中缀、后缀表达式
定义
中缀表达式是一个通用的算术逻辑表示法,是最常见的一种表达式,如5*(2+3)-4;
前缀表达式是一种没有括号的算术表达式,与中缀表达式不同的是,其将运算符写在前面,操作数写在后面,如上述表达式的前缀表示为- * 5 + 2 3 4
后缀表达式不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行,上述表达式的后缀表示为5 2 3 + * 4 -
中缀、前缀、后缀表达式分别对应着二叉树的中序、前序、后序遍历,如何通过中缀表达式建立二叉树呢?可以参考这里:http://blog.csdn.net/wzy_1988/article/details/11179281,这里就不做过多叙述,至于如何用代码来实现,后续二叉树的文章中会有介绍,先挖个坑。
如何计算值前缀、后缀、中缀表达式
首先需要明确的一点是,对于人来说,中缀表达式是很好计算的,而对于计算机来说,前缀表达式和后缀表达式更好计算值。
计算前缀表达式
如前所述的前缀表达式- * 5 + 2 3 4,从右到左扫描,如果遇到操作数则进栈,如果遇到运算符,则弹出两个栈顶元素进行运算,并将结果入栈,直到扫描结束:
(1)将4 3 2 分别入栈
(2)将2 3出栈,2+3=5,将结果5入栈
(3)将5入栈
(4)将5 5出栈,5*5=25,将结果25入栈
(5)将25 4出栈,25-4=21,即21,为最终结果
注意:运算时第一个出栈元素放在运算符的左边,第二个放在右边
计算后缀表达式
后缀表达式的计算与前缀表达式相似,从左到右扫描,如果遇到操作数则进栈,如果遇到运算符,则弹出两个栈顶元素进行运算,并将结果入栈,直到扫描结束,后缀表达式5 2 3 + * 4 -的计算过程如下:
(1)将5 2 3进栈
(2)将3 2出栈,2+3=5,将结果5入栈
(3)将5 5出栈,5*5=25,将25入栈
(4)将4进栈
(5)将4 25出栈,25-4=21,即得到结果
注意:运算时第一个出栈元素放在运算符的右边,第二个放在左边
计算中缀表达式
定义两个栈,operatorStack放运算符,operandStack放操作数,从左到右扫描中缀表达式:
(1)如果是操作数,则进栈
(2)如果是运算符
(2.1)如果是左括号或operatorStack栈为空或栈顶运算符为左括号,进栈
(2.2)如果是右括号,两个栈顶操作数出栈,栈顶运算符出栈,将计算结果进栈,直到出栈的运算符是左括号为止
(2.3)如果是其他情况,判断与栈顶运算的优先级,如果大于栈顶运算符,则进栈;如果小于,两个栈顶操作数出栈,栈顶运算符出栈,将计算结果进栈,最后将该运算符进栈
(3)扫描完成,判断运算符栈是否为空,不为空则不断弹出两个操作数和一个运算符,将结果入栈,直到运算符栈为空
(4)操作数栈中剩下的一个数即为结果
下面以计算5*(2+3)-4为例:
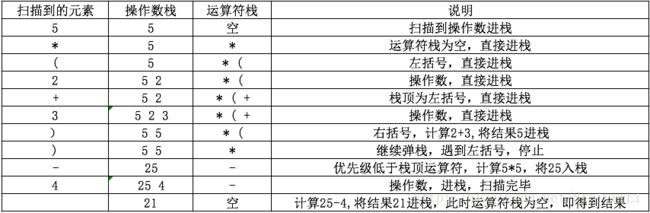
中缀转后缀
步骤:
(1)创建一个栈存放运算符,用String类对象postfix将结果拼接起来。
(2)从左到右扫描中缀表达式
(3)如果是操作数,拼接到postfix
(3.1)如果是左括号或栈为空,直接进栈
(3.2)如果是右括号,栈顶元素出栈,拼接到postfix,直到左括号出栈,但左括号不输出
(3.3)如果是其他运算符,比较与栈顶运算符的优先级,如果大于,进栈,如果小于或等于,栈顶元素出栈并拼接到postfix,将该运算符进栈
(4)扫描完成后,将栈中是运算符全部拼接的str
下面以5*(2+3)-4为例:
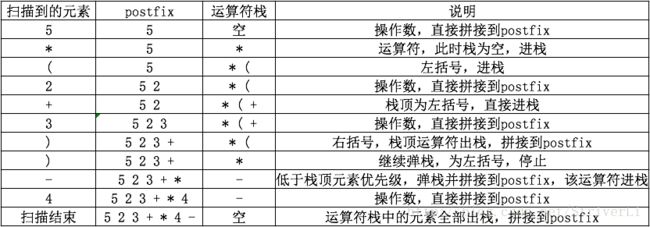
中缀转前缀
与中缀转后缀相似,不同点在于因为要从右到左扫描,先遇到的是右括号。而且最后拼接的结果与预期结果正好相反,因此需要另一个栈result存放中间结果,还有一个不同点在于比较运算符的优先级时,相同优先级也要进栈,步骤如下:
(1)创建一个栈存放运算符,创建一个result栈存放中间结果
(2)从右到左扫描中缀表达式
(3)如果是操作数,压入result栈
(3.1)如果是右括号或栈为空,直接进运算符栈
(3.2)如果是左括号,栈顶元素出栈,压入result栈,直到右括号出栈,但右括号不输出
(3.3)如果是其他运算符,比较与栈顶运算符的优先级,如果大于或等于,进栈,如果小于,栈顶元素出栈并压入result栈,然后该运算符压入运算符栈
(4)扫描完成后,将运算符栈中的剩余元素压入result栈
下面以5*(2+3)-4为例:

下面是所有代码:
public class Calculator {
/**
* 1、包含计算前缀、后缀、中缀表达式的方法
* 2、包含中缀转前缀、中缀转后缀的方法
* 3、包含一些辅助操作,如计算运算符的优先级、获取操作数等
* 4、注意,如果直接输入前缀表达式或后缀表达式,每一项之间用空格分开,
* 否则无法计算含有两位及以上的操作数的表达式,因为不知道哪几个数字组成一个数
* 5、本例中使用的栈为自定义栈,也可以用java提供的位于java.util包下的Stack
* 6、为减少代码并方便测试,将三个成员变量设置为public类型。
*/
public String prefix = ""; // 前缀表达式
public String nifix = ""; // 中缀表达式
public String postfix = ""; //后缀表达式
public void nifix2Prefix(){ // 中缀表达式转前缀表达式
StringBuilder str = new StringBuilder();
DynArrayStack stack = new DynArrayStack<>();
DynArrayStack result = new DynArrayStack<>();
for(int j = nifix.length()-1; j >= 0; j--){
char c = nifix.charAt(j);
if(!isOperator(c+"")){ // 如果是操作数
int i = readDoubleReverse(j);
String temp = nifix.substring(i+1, j+1);
result.push(temp);
j = i+1;
} else {
if(stack.isEmpty() || c == ')' || stack.getTop() == ')'){
stack.push(c);
} else if(c == '('){
char op = stack.pop();
while(op != ')'){
result.push(op + "");
op = stack.pop();
}
} else {
if(getPriority(c) >= getPriority(stack.getTop())){
stack.push(c);
} else {
result.push(stack.pop() + "");
stack.push(c);
}
}
}
}
while(!stack.isEmpty()){
result.push(stack.pop() + "");
}
while(!result.isEmpty())
prefix += result.pop() + " ";
}
public int readDoubleReverse(int i){ // 反向读取操作数,中缀转前缀时使用
for(; i >= 0; i--){
char c = nifix.charAt(i);
int count = 0;
if(count == 2){
throw new NumberFormatException("输入的数据有误");
}
if(c == '.'){ // 小数点
count++;
} else if(isOperator(c+"")){ // 如果是运算符
break;
}
}
return i;
}
public void nifix2Postfix(){ // 中缀表达式转后缀表达式
DynArrayStack stack = new DynArrayStack<>();
for(int j = 0; j < nifix.length(); ++j){
char c = nifix.charAt(j);
if(!isOperator(c+"")){ //如果是操作数
int i = readDouble(j);
String temp = nifix.substring(j, i);
postfix += temp + " ";
j = i-1;
} else { // 如果是运算符
if(c == '(' || stack.isEmpty()){
stack.push(c);
} else if(c == ')') {
char op = stack.pop();
while(op != '('){
postfix += op + " ";
op = stack.pop();
}
} else {
if(getPriority(c) > getPriority(stack.getTop())){
stack.push(c);
} else {
postfix += stack.pop() + " ";
stack.push(c);
}
}
}
}
while(!stack.isEmpty()){
postfix += stack.pop() + " ";
}
}
public double calculateNifix(){ // 计算中缀表达式
DynArrayStack operatorStack = new DynArrayStack<>(); // 存放运算符
DynArrayStack operandStack = new DynArrayStack<>(); // 存放操作数
for(int j = 0; j < nifix.length(); ++j){
char c = nifix.charAt(j);
if(!isOperator(c+"")){ // 如果是操作数
int i = readDouble(j);
String temp = nifix.substring(j, i);
operandStack.push(Double.parseDouble(temp));
j = i-1;
} else { // 如果是运算符
if(c == '(' || operatorStack.isEmpty() || operatorStack.getTop() == '('){
operatorStack.push(c);
} else if(c == ')') {
char operator = operatorStack.pop();
while(operator != '('){
double a = operandStack.pop(); // 放在运算符的右边
double b = operandStack.pop(); // 放在左边
String s = operator+"";
operandStack.push(calculate(b, a, s)); // 计算结果进栈
operator = operatorStack.pop();
}
} else {
if(getPriority(c) > getPriority(operatorStack.getTop())){
operatorStack.push(c);
} else {
double a = operandStack.pop(); // 放在运算符的右边
double b = operandStack.pop(); // 放在左边
String s = operatorStack.pop()+"";
operandStack.push(calculate(b, a, s)); // 计算结果进栈
operatorStack.push(c);
}
}
}
}
while(!operatorStack.isEmpty()){ // 当存放运算符的栈不为空时
char c = operatorStack.pop();
double a = operandStack.pop(); // 放在运算符的右边
double b = operandStack.pop(); // 放在左边
String s = c+"";
operandStack.push(calculate(b, a, s)); // 计算结果进栈
}
return operandStack.pop();
}
public int readDouble(int i){ // 正向读取操作数
for(; i < nifix.length(); ++i){
char c = nifix.charAt(i);
int count = 0;
if(count == 2){
throw new NumberFormatException("输入的数据有误");
}
if(c == '.'){ // 小数点
count++;
} else if(isOperator(c+"")){ // 如果是运算符
break;
}
}
return i;
}
public int getPriority(char c){ // 获取运算符的优先级
switch (c) {
case '*':
case '/':
return 2;
case '+':
case '-':
return 1;
default:
return -1;
}
}
public double calculatePostfix(){ // 计算后缀表达式
DynArrayStack stack = new DynArrayStack<>();
String[] arr = postfix.split(" ");
for(int i = 0; i < arr.length; i++){
if(isOperator(arr[i])){ // 如果是运算符
double a = stack.pop();
double b = stack.pop();
double temp = calculate(b, a, arr[i]);
stack.push(temp);
} else {
stack.push(Double.parseDouble(arr[i]));
}
}
return stack.pop();
}
public double calculatePrefix(){ // 计算前缀表达式
DynArrayStack stack = new DynArrayStack<>();
String[] arr = prefix.split(" ");
for(int i = arr.length-1; i >= 0; i--){
if(isOperator(arr[i])){ // 如果是运算符
double a = stack.pop();
double b = stack.pop();
double temp = calculate(a, b, arr[i]);
stack.push(temp);
} else {
stack.push(Double.parseDouble(arr[i]));
}
}
return stack.pop();
}
public boolean isOperator(String s){ // 判断是否是运算符
return s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/") || s.equals("(") || s.equals(")");
}
public double calculate(double a, double b, String s){ // 计算
switch (s) {
case "*":
return a*b;
case "/":
return a/b;
case "+":
return a+b;
case "-":
return a-b;
default:
return -1;
}
}
} 完整代码可访问我的GitHub:https://github.com/StriverLi/Data-Structures-and-Algorithms-in-Java/tree/master/src/stack

