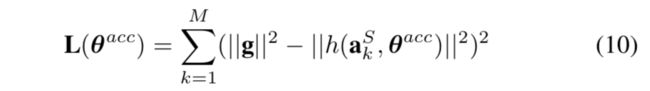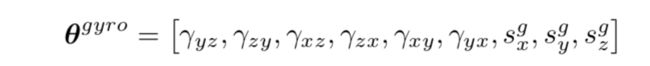IMU（惯性测量单位）是机器人中非常流行的传感器：其中，它们被用于惯性导航[1]，姿态估计[2]和视觉惯性导航[3]，[4]，也使用 智能手机设备[5]。 机器人技术中使用的IMU通常基于MEMS（微机电系统）技术。 它们由一组三轴簇组成：加速度计，陀螺仪和磁力计簇。
我们的程序利用了多位置方法的基本思想，首先在[7]中提出了加速度计校准：在静态位置，测量加速度的范数等于引力的大小加上多个 源误差因子（即，它包括偏差，未对准，噪声......）。 所有这些数量都可以通过一组静态态度的最小化来估算。 在加速度计三元组的校准之后，我们可以使用由加速度计测量的重力矢量位置作为校准陀螺仪三元组的参考。 通过积分两个连续静态位置之间的角速度，我们可以估计新方向的重力位置。 最终获得陀螺仪校准，最小化这些估计与校准加速度计给出的重力参考之间的误差。
在此过程中，陀螺仪的校准精度很大程度上取决于加速度计校准的准确性，并将其用作参考。 此外，信号噪声和偏差应对校准精度和用于检测校准中使用的实际静态间隔的算法的可靠性产生负面影响。 最后，一致的数值积分过程对于减轻信号离散化的影响至关重要，通常以100 Hz采样。 在我们的方法中，我们面临这些问题，引入了对标准多位置方法的以下修改：
建议的校准协议利用周期缩短的大量静态状态，以增加数据集的基数，同时保留传感器偏差的局部稳定性假设
如[8]中所提出的，我们使用Allan方差估计了陀螺仪偏差漂移
我们介绍了一种简单但有效的静态探测器，它利用传感器噪声幅度，固定时间采样窗口和切割阈值，在优化框架内自动估算
我们采用Runge-Kutta数值积分方法来提高陀螺仪校准的准确性。
我们使用受可变偏差，未对准，比例因子误差和噪声影响的合成数据对我们的系统进行了广泛测试。 在所有情况下，我们都获得了稳定而准确的结果。 此外，我们使用其原始未校准数据作为输入，对商业化，工厂校准的Xsens MTi IMU进行了校准。 我们的校准结果与设备校准证书报告的工厂参数相当。
传统上，IMU的校准是通过使用特殊机械平台（例如机器人操纵器），以一组精确控制的方向移动具有已知旋转速度的IMU来完成的[9]，[10]，[11]。 在每个方向上，将加速度计的输出与预先计算的重力矢量进行比较，而在旋转期间，将陀螺仪的输出与预先计算的旋转速度进行比较。 然而，用于校准的机械平台通常非常昂贵，导致校准成本经常超过IMU硬件的成本。
在[12]中，已经提出了利用基于标记的光学跟踪系统的校准程序，而在[13]中，GPS读数用于校准初始偏差和未对准。显然，这些方法的准确性很大程度上取决于所采用的运动参考（即，运动捕捉系统或GPS）的准确性。 Lotters等人首次提出了多位置方法。 [7]：他们提出使用静态加速度的大小必须等于重力的大小来校准加速度计的偏差和比例因子。该技术已在[14]和[15]中扩展，以包括加速度计轴未对准。他们为陀螺仪提出的误差模型类似于用于加速度计的误差模型，但在这种情况下的校准过程需要单轴转盘来提供强旋转速率信号，从而提供高校准精度。不幸的是，这些方法不仅需要机械设备，而且两个三元组是独立校准的，并且不能检测它们之间的不对准。在[8]和[16]中，作者提出了两种不需要任何外部机械设备的校准方案。与我们的方法类似，在第一项工作中，作者利用重力矢量幅度的高局部稳定性校准加速度计，然后比较校准加速度计检测到的重力矢量与通过积分角速度获得的重力矢量获得陀螺仪校准。在第二部作品中，作者还利用了磁场的局部稳定性。
Hwangbo等[17]最近提出了一种基于迭代矩阵分解的自校准技术。 他们使用重力作为加速度计参考，并使用相机作为陀螺仪参考。
对于理想的IMU，加速器三元组的3个轴和陀螺仪三元组的3个轴定义了一个共享的正交三维框架。每个加速度计都可以检测沿着一个不同轴的加速度，而每个表面 相同的轴。由于装配不兼容，在实际IMU中不幸的是，两个三元组形成两个不同的（即，未对准的）非正交的帧。单个传感器也不完美：通常使用的缩放因子 对于相同传感器的不同实例，传感器的实际物理量是不同的，而制造商仅提供默认的标称比例因子。此外，输出信号也几乎总是受非零影响。
我们可以通过以下方式定义两个相关的正交，理想帧（AF）和陀螺仪帧（AF）以及陀螺仪帧（AF）和陀螺仪帧（AF）以及陀螺仪帧（AF）和陀螺仪帧（AF）：
•AOF的x轴和AF的x轴重合
•AOF的y轴位于AF的x轴和y轴所跨越的平面中。
对于陀螺仪，分别用GF和GOF替换AF和AOF缩写词就足够了。最后，我们定义一个体帧（BF），它是一个正交帧，用于表示例如I帧的坐标系。 对于小角度，非正交帧（AF或GF）中的测量sS可以是过渡底盘。车身框架通常与AF和GF框架的角度不同，但通常，它们之间没有直接关系。 在正交体框架中（有关推导的细节，见[18]）：
其中sB和sS表示特定的力（加速度），
这里，βi是围绕第j个BF轴的第i个加速度计或陀螺仪轴的旋转，参见图2.等效地，在车身框架坐标和加速器（或陀螺仪）中的旋转速度坐标。
另一方面，两个正交帧BF和AOF（以及等效地，BF和GOF）通过纯旋转相关。
在加速度计情况下方程1：进来：提出校准方法，我们假设车身框架。
我们改变了字母β，参考一般情况，用字母α表示加速器情况，而aO和aS表示AO和AF3中的特定加速度。
如前所述，陀螺仪和加速度计测量应该参考相同的参考系，在我们的例子中是AOF。然后，使用公式1，对于陀螺仪，我们有：
其中ωO和ωS在透视中注意AOF和GF中的特定角速度。引入了两个缩放矩阵。加速器和陀螺仪都受到偏差和比例误差的影响。
III. BASIC CALIBRATION FRAMEWORK
为了校准加速度计三元组，我们需要估计以下未知参数向量：
我们定义以下函数：
在这里，我们可以忽略测量噪声，因为在我们的校准过程中，我们在每个静态间隔中应用信号平均。
其中|| g || 是可以从特定公共表格中容易地恢复的局部重力矢量的实际大小（例如，知道我们正在执行校准的位置的纬度，经度和高度）。 为了最小化Eq。 10，我们采用Levenberg-Marquardt（LM）算法。
为了校准陀螺仪三元组，我们可以假设系统无偏置，在适当的无运动初始阶段简单地平均静态陀螺仪信号。 以下关于艾伦方差的讨论证明了这一点（参见第IV-C节）。 此外，由于我们需要使用加速度计作为已知参考，我们使用上面计算的校准参数θacc，用公式9校正加速度计读数。
我们定义运算符Ψ，它将n个陀螺仪读数ωSi的序列和由校准的加速度计给出的初始重力值ua，k-1（即表示重力方向的单位矢量）作为输入，并返回最终的重力值 ug，k，使用第k-1和第k个静态区间之间的陀螺仪测量值计算：
Ψ可以是任何积分算法，通过积分输入角速度来计算最终方向。 我们需要估算的未知参数矢量来校准陀螺仪：
在这种情况下，我们可以将成本函数定义为：
IV. CALIBRATION PROCEDURE
如第一部分所述，建议的校准框架工作需要收集一个数据集，其中包含原始加速器和陀螺仪读数的流，当操作员将IMU移动到不同的静态位置时，以便生成一组离散、温度稳定、旋转。我们的校准协议的简单图表如图1所示。如第III节所述，为了减轻Eq 10和Eq 13最小化时的噪声影响，我们需要在适当的时间间隔内对信号进行平均。 这施加了静态间隔长度的下限（图1中的twait）。没有运动的初始化周期（T init 1）也是必不可少的：这将被用来表征陀螺仪的偏差（第四节 - C）和静态探测器操作员（Sec IV-A）。
A. Static Detector
校准的准确性高度依赖于静态和运动间隔之间分类的可靠性：校准加速器我们使用静态间隔，而对于陀螺仪校准，我们还包括两个连续静态间隔之间的运动间隔。更重要的是，[8]中需要使用准静态探测器，在真实数据集中表现不佳：检测到的静态间隔通常包括一小部分运动。此外，它们需要微调，因为 取决于三个参数。
我们建议使用基于方差的静态检测器算子，它利用上面介绍的静态区间长度的下限。我们在加速度计信号上有探测器：给定一个长度为twait秒的时间间隔（见图1），对于每个加速器样本（atx，aty，atz），在时间t，我们计算方差，
其中vartw（at）是一个运算符，它以t为中心的长度为tw秒的时间间隔计算一般信号的方差。我们在静态和运动间隔之间进行分类，只需检查ζ（t）的平方是否低于或大于阈值。作为阈值，我们考虑方差幅度ζinit的整数倍，在所有初始化时段Tinit上计算。在所有实验中，我们使用tw = 2秒，而使用Allan方差估计Tinit（参见第IV-C节）。值得注意的是，我们的静态检测器不需要任何参数调整：分类中使用的整数乘数由我们的校准算法自动估算（参见第IV-D节）。图3报告了我们的静态滤波器如何处理实际数据的示例：在这种情况下，估计的整数乘数为6。
D. Complete Procedure
为了避免校准参数估计中的不可观察性，必须收集至少九种不同的高度[15]（例如，图1）。根据我们的经验，为了获得更好的校准结果，需要更多N个不同的态度，同时保持减少每个静态间隔的持续时间，以保持陀螺仪偏差的时间稳定性。在36≤N≤501N≤twait≤4sec的情况下，我们在校准精度，偏差稳定性和降噪之间取得了良好的平衡。初始化周期Tinit的持续时间由Allan方差分析给出（见Sec）IV-C）。校准协议总结在图1中，而在算法1中，报告校准算法的伪代码。
V. EXPERIMENTS
我们用合成数据和实际数据测试了我们的方法。 在模拟中，我们可以将结果与完美的地面实况进行比较，即无噪声，无失真信号，而校准矩阵是已知的。 使用真实数据集，我们将估计的校准参数与IMU数据表中报告的校准参数进行比较。