毕业复习计划 - 数据结构 (2) B-Tree
从概念性的思维来审视, 无疑会认为R-树是一种十分平衡的设计, 既保持了查询的优点, 又不牺牲太多的修改效率, 除了因为颜色属性略占空间外(即使这一点也仅是在大数据量时才予考虑的, 当然大数据量正是B树适用的场景), 作为构造一个Key查询功能的结构的方法, R-B树简直无可挑剔. 可惜, 事实是, 没有万能的数据结构, 当我们的数据量过大而必须使用辅助存储时, 最好是另想办法 —— 总不能指望靠操作系统的内存管理机制来"透明"实现吧. "透明"的一个隐含的贬义即"低效".
B-tree就是用来解决数据量大于贮存而不得不放在辅助存储器的问题, 算法将读写主动控制起来, 而数据结构的设计将数据分割、组织成为易于存取的结构. B-tree为了减少磁盘读写, 在单个节点中存放多个键值, 而一个节点的数据大小设计为辅存中存储单元的整数倍, 进一步优化磁盘读写. 节点内键值按单增排序, 每两个键值间保存指针指向子节点(子树), 子树中所有键值的大小都在该二键值之间. 这种设计的好处是, 如果节点内保存1000个键值, 那么在10亿个键值的集合查询, 仅需读取两个node(两次磁盘访问).
关于节点大小与树高的关系是这样的. B-tree最重要的全局属性是branching factor(分支因数?), 它定义了内结点中键值的数量范围以及子节点的数量范围. 设此系数为t, 则任何内节点的键值数k>t-1且k<2t-1, 子节点数为k+1, 而树高渐进为logt((n+1)/2), n为树中全部节点数.
Branching factor的重要性表现在, 对树的操作(插入/删除), 必须保证操作的完成不得使节点内键值分布超出允许的范围, 这一点与其他的平衡树类似, 都是为了保持树结构的稳定, 防止操作效率恶化.
B-tree的节点键值数有两个边界, 操作过程中就必须处理两种可能的越界. 分别定义了两种操作来维持节点大小, 分别在插入和删除操作中使用. 1. 插入使得节点键值过多(>2t-1), 需要进行分裂操作, 将插入后会造成上越界的节点一分为二, 再按照一般的插入步骤插入到二者之一. 2. 删除操作可能造成节点键值过少(
插入的图示
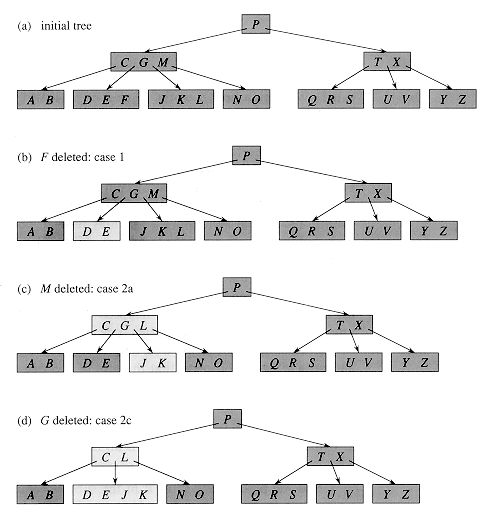
删除的图示(摘自introduction to algorithm)