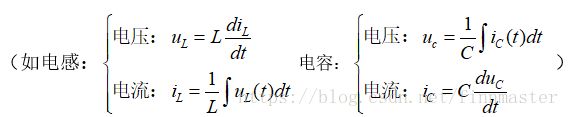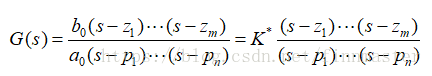6-5_自控学习
自动控制原理
一.控制系统的数学模型
(1)时域下的数学模型——微分方程
1.列写元件的微分方程(时域分析中常用的数学模型)
步骤:1)根据元件的工作原理及其在控制系统中的作用,确定其输入量和输出量;
2)分析元件工作中所遵循的物理规律,列写相应的微分方程;
(如基尔霍夫电压电流定律)
3)消去中间变量,得到输出量和输入量之间关系的微分方程,便是元件时域的数学模型。
一般情况下,应将微分方程写为标准形式,即与输入量有关的项写在方程的右端,与输出量有关的项写在左端,两端变量的导数项均按降幂排列。
2.线性系统的基本特性
用线性微分方程描述的元件或系统,称为线性元件或线性系统,其重要性质:可以应用叠加原理(可加性和齐次性)
3.线性定常微分方程的求解
为了了解系统输出量随时间变化的特性。求解方法由:经典法和拉普拉斯变换法。
(2)复数域下的数学模型——传递函数
传递函数不仅可以表征系统的动态性能,而且可以用来研究系统的结构或参数变化对系统的影响。
1.线性定常系统(线性——可加性与齐次性;定常——导数前系数为常数)传递函数定义:在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比。
特点:用系统参数表示输出量与输入量之间的关系,只取决于系统或元件的结构和参数,而与输入量的形式无关,也不反映系统内部的任何信息。
2.传递函数的零点与极点
传递函数的分子多项式和分母多项式经因式后可以写成如下形式:
传递函数分子多项式的零点,称为传递函数的零点;
分母多项式的零点,称为传递函数的极点
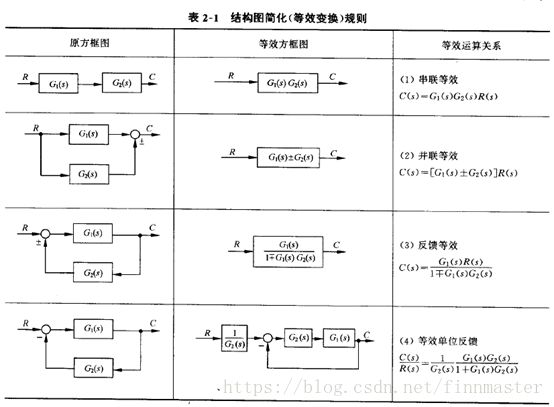
(3)控制系统的结构图与信号流图
方框间的基本连接方式只有串联,并联和反馈连接三种。
以上三种简化:
在信号流图中,有常用的名词术语:源节点(输入节点),阱节点(输出节点),混合节点(既有输入又有输出),前向通路(从输入节点到输出节点传递时,每个节点只通过一次的通路,叫前向通路),回路(起点与终点在同一个节点)
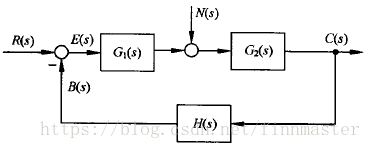
(4)闭环系统的传递函数
二.线性系统的时域分析法
(1)典型输入信号
典型的输入信号,是指根据系统常遇到的输入信号形式,在数学描述上加以理想化的一些基本输入函数。
注意:一般认为,阶跃输入对系统来说是最严峻的工作状态,如果在其作用下动态性能满足要求,那么系统在其他形式的函数作用下,其动态性能也是令人满意的。
(2)动态性能与稳态性能
为了评价线性系统时间响应的性能指标,需要研究控制系统的典型输入信号作用下的时间响应过程。
动态性能:
动态过程又称为过渡过程或瞬态过程,指系统在典型输入信号下,系统输出量从初始状态到最终状态的响应过程。
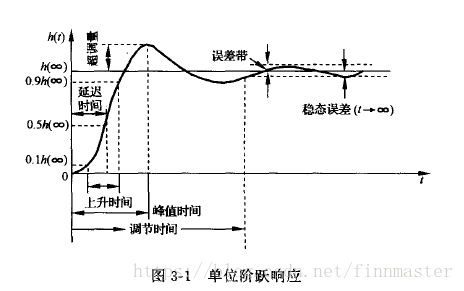
在实际应用中,常用的动态性能指标多为上升时间或峰值时间(评价系统的响应速度),调节时间(综合评价响应速度和阻尼程度)和超调量(系统的阻尼程度)。
稳态性能:
稳态过程又称稳态响应,指系统在典型输入信号作用下,当t趋于∞时,系统输出量的表现方式。
稳态误差是稳态性能的一种性能指标。若时间趋于无穷,系统输出量不等于输入量或输入量的确定函数,则系统存在稳态误差。
(3)一阶系统的时域分析
一阶惯性系统一般由一个储能元件(电感,电容)与一个耗能元件(电阻)的组合,就构成了一个惯性系统。
当输入量突然发生突变时,输出量不能突变,只能按着指数规律逐渐变化,这表明该环节具有惯性。
单位脉冲函数与单位阶跃函数的一阶导数及单位斜坡函数的二阶导数的等价关系,对应有单位脉冲响应与单位阶跃响应的一阶导数及单位斜坡响应的二阶导数的等价关系。
系统对输入信号导数的响应,就等于系统对该输入信号响应的导数;或者,系统对输入信号积分的响应,就等于系统对该输入信号响应的积分而积分常数由零输出初始条件确定。
故而研究线性定常系统的时间响应,不必对每种输入信号形式进行测定和计算,往往只取其中一种典型形式进行研究。