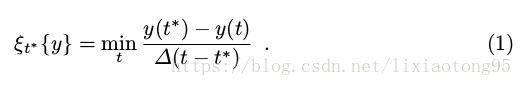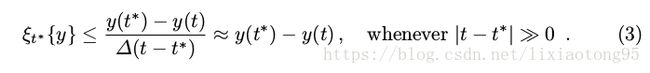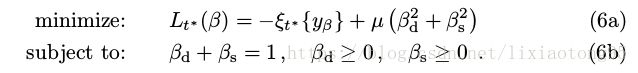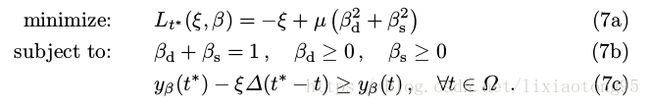揭开深度跟踪的力量--Unveiling the Power of Deep Tracking (ECCV2018)

论文地址：Goutam_Bhat_Unveiling_the_Power_ECCV_2018_paper

 

文章亮点：

1、分析深度特征和浅层特征对跟踪器性能的影响；

2、探究跟踪器鲁棒性和准确性之间的平衡；

3、提出新的深浅特征的融合策略；

另：研究数据增强策略对跟踪器性能的提升。

深度特征的优点：能够编码高级抽象信息，不受复杂外观变化和杂波的影响，鲁棒性好。

深度特征的局限：需要大量数据；定位准确度低；跟踪任务中更深更复杂的网络架构无益。

因此，许多跟踪器通过浅层激活或手工制作的特征来补充深度特征表示，以提高定位精度。

 

一、分析深度特征和浅层特征对追踪器的影响：

以ECO算法为基准，数据集：OTB-2015；浅层特征：HOG、CN；深度特征：ResNet-50第四卷积层的激活；研究不同数据增

强技术对浅层和深层特征的影响：

翻转：样品水平翻转

旋转：从固定的12个角度旋转，范围从-60°到60°

平移：在特征提取之前水平和垂直移动n个像素，生成的特征映射向后移动n/s像素，s是步幅。

模糊：使用高斯滤波器模糊，模拟运动模糊和比例变化。

Dropout：将20％的特征通道随机设置为零，剩余的特征通道被放大以保持样本能量。

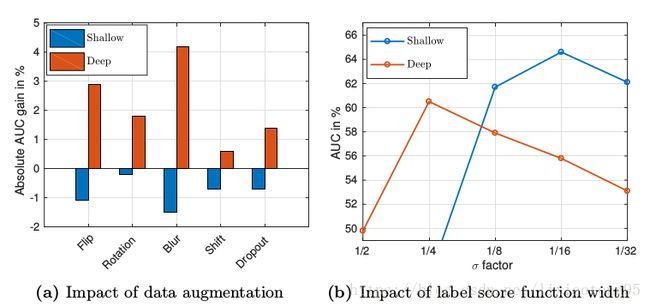
图(a)展示了各增强策略对跟踪性能的影响(AUC分数)，容易看出：深度特征始终受益于数据增强。浅层特征则未受益。深度和

浅度特征表现出明显的差异，是因为深度特征捕获更高级别的语义信息，这些信息对增强的数据（如“翻转”）不变，因此可以从

增加的训练数据中获得提升；而浅层特征提取的低级信息受到像'翻转'或'模糊'这样的增强的阻碍，就会使性能有所下降。

 

二、分析深度或浅层特征对准确性-鲁棒性平衡的影响：

基于DCF的跟踪器如ECO，提取正样本的区域大小由标签得分函数的宽度控制。

ECO中采用的是高斯函数，标准偏差与目标大小成比例，系数为σ。

实验对比了深层和浅层特征在不同σ值下的性能。

实验结果如图(b)所示，当σ值高时，深度特征被很好地利用，其中σ=1/4时结果最佳。

可以理解为深度特征的不变性对小变化鲁棒，这就导致深度特征在准确性上表现不佳。

当σ值较低时，浅层特征表现良好，随着σ增加，浅层特征模型性能下降。

这是因为浅层特征捕获的是低水平高分辨率的特征，因此非常适合提高定位精度，

且它们对小变换敏感，所以处理高σ值正样本时性能较差。

 

结论：

深度模型可以通过数据增强策略+高σ值(宽的标签函数)提高鲁棒性，而不是准确性。而数据增强策略对浅层特征模型没有帮

助，且低σ值(窄的标签函数)时性能良好，即浅层特征鲁棒性差，但准确性好。

实验结果明显地表现出深度和浅层特征的互补特性。因此，应将浅层和深层模型独立训练，之后再做进一步融合。

即：

1、广泛的数据增强可以为基于深度特征的模型带来显着的性能提升，但同时通常损害浅层特征模型的性能。

2、深度模型应该训练稳健性，浅层模型应该强调准确的目标定位。

3、深层和浅层模型应该独立训练并在后期融合。

三、新的深浅特征的融合策略：

主旨：自适应地找到每个模型的最佳权重来融合这些分数，从而产生清晰且明确的分数函数。

如前所述，深度和浅度模型在准确性和鲁棒性方面具有不同的特征。我们提出了一种新的自适应融合方法，基于预测质量衡量

指标，充分利用它们的互补性。

(1) 预测质量衡量：prediction quality measure

预测质量测量指标应当同时奖励目标预测的准确性和鲁棒性。准确度与预测周围的检测得分清晰度有关，更尖锐的峰值表示更

准确的定位能力。鲁棒性来自预测值相对于干扰峰值的余量。如果余量(距离)很小，则预测不明确，余量很大，则表明预测的置

信度显着高于其他候选位置。文章提出最小加权置信区间作为候选目标预测t *的质量衡量，如式(1)所示：

从式(1)中可以看出，当且仅当y(t*)是y的全局最大值时，ξt* {y}≥0 。分子是候选预测t *处的置信度得分y（t *）与位置t处的得分

y（t）之差。位置t*和t之间的距离作为权值，由距离测量函数Δ计算得到，且距离测量函数Δ满足在范围内，有

Δ(0) = 0,　且lim |τ|→∞时，Δ(τ) = 1。还假设Δ是二阶连续可微分，并且在τ= 0时具有正定的Hessian矩阵。因此，构造出式(2)

中的函数作为测量函数Δ：

其中，κ是在|τ|增加时控制Δ(τ)→1转变速度的参数。可以验证，式(2)的数学性质满足我们的需求：

 

当t远离预测t*时，即| t - t* | »0时：

因而，质量衡量值ξt* {y}近似地受到与预测 t* 的直接连续邻域之外的最重要的干扰峰值y(t)的得分差异的限制。因此，质量衡量

值ξt* {y}高时，对应于预测时没有较大的干扰项的情况，即鲁棒性高。相反，如果存在具有相似得分 y(t) ≈ y(t*) 的二次检测峰值

y(t)，则预测衡量指标量很低，即ξt* {y}≈0。

 

当t→t*时, 我们认为预测值t*是y的局部最大值(极值点)。将y的梯度和Hessian分别表示为∇y(t)和Hy(t)。于是有∇y(t*) = 0且

0≥λ*1≥λ* 2，其中λ* 1，λ* 2是Hy(t*)的特征值。把式(2)代入，则有：

特征值|λ* 1|表示在峰值t*处的得分函数y的最小曲率。因此，|λ*1|是衡量峰值t*处的锐度指标。质量衡量值ξt*{y}与锐度|λ*1|成正

比。因此，质量衡量值ξt*{y}高时，对应于峰值是陡峭、精确的，而平坦峰值对应低质量值，即模糊不准确的定位预测。参数κ

用于控制鲁棒性和准确性之间的权衡。

 

(２) 自适应的融合策略：

基于上述提出的质量衡量指标的进行深层和浅层特征的自适应融合，来找到最优状态。融合得分由两个得分的加权组合得到：

其中β=(βd，βs)分别是深度模型和浅层模型分数的权重。我们的目标是联合估计最大化质量测量的分数权重β和目标状态t*。

这个问题可以通过最小化损失来实现，即：

后面的平方和项是一个由参数μ控制的正则化项，用于惩罚较大的权重偏差。为了优化（6），引入了松弛变量ξ=ξt* {yβ}，将问

题等效为：

对于任何一个已知状态t*，式(7)对应一个二次规划（QP）问题，可用标准方法解决。实践中，我们根据深度和浅层得分的局部

最大值对有限的候选状态Ω进行采样。随后，通过求解三参数QP问题，对每个状态t*∈Ω优化问题(7)，然后选择总损失最低的

候选状态t *作为最终预测值。

 

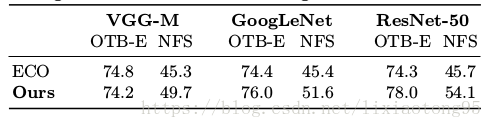
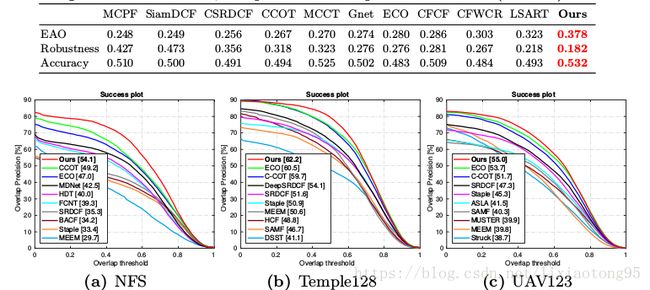
四、实验结果详见论文

五、总结：

系统分析了视觉跟踪深度特征性能的关键影响因素。实践证明了单独训练浅层和深层特征对于获得高鲁棒性和准确性至关重

要。并进一步提出了新的融合策略，结合深度和浅层外观模型来利用它们的互补特征。实验结果证明了方法的有效性。