【算法】彻底搞懂(括号匹配)——图解带你直击本质
括号匹配专题
你可否记得,当年被【括号匹配】支配的恐惧?
>>> 本文先讨论最基本的括号匹配及其经典的【栈】思路
>>> 再分析其变体
>>> 最后是究极变体,从【栈】【动态规划】【括号计数(追赶法)】三种方法切入,彻底理解括号匹配问题
>>>
>>> 记住,所有的方法,归根结底还是从括号字符串的自身特性出发的
>>> 再记住两句话:
>>> 1.【尝试用')'去消去前面的'('】
>>> 2.【当右括号数量超过左括号时,必然串无效】
/*
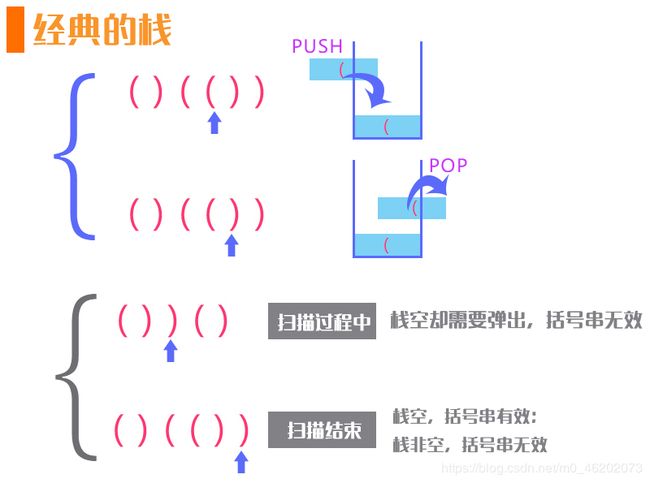
* 经典的【栈】思路
*
* 遇到'(',就入栈; 遇到')',就出栈
* 扫描过程中,当出栈时发现栈空时,串无效
* 扫描结束后。若栈空,则串有效;如果栈不空,则串有效
*/
public boolean isValid(String s) {
Deque<Character> stack = new ArrayDeque<>();
for(char c : s.toCharArray()) {
if(c == '(') {
stack.push(c);
}else {
if(stack.isEmpty()) {
return false;
}else {
stack.pop();
}
}
}
return stack.isEmpty();
}
变体1——不止是小括号
思路变体:【经典的栈】 + 【Map】
▊【Q20】(ez) 有效的括号(括号匹配问题)
给定一个只包括 ‘(’,’)’,’{’,’}’,’[’,’]'的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 注意空字符串可被认为是有效字符串。
示例 1:
输入: “([{}])”
输出: true
示例 2:
输入: “([)]”
输出: false
class Solution {
public boolean isValid(String s) {
/*
* 思路:
* 如果是左括号,就毫不犹豫的入栈;
* 如果是右括号,不仅要先判断是否栈空,还要判断弹出的左括号是否对应此时的右括号
*
* 注:
* 1.使用HashMap进行匹配,使得代码和逻辑都更具美感
* 2.典型的栈结构问题。由于java 8,9有移除Stack的趋势,因此这里使用双端队列Deque,同样有PushPop特性
*/
if(s == null || s.length() == 0) return true; // leetcode传统艺能,null和0值不说就是true
Map<Character, Character> map = new HashMap<>();
map.put(')', '(');
map.put(']', '[');
map.put('}', '{');
Deque<Character> dq = new ArrayDeque<>();
for(char c : s.toCharArray()){
if(c == '(' || c == '[' || c == '{'){
dq.push(c);
}else{
if(dq.size() == 0 || map.get(c) != dq.pop()) return false;
}
}
return dq.size() == 0;
}
// 另外:栈中的字符串必定是'(',因此在这个简单的括号匹配问题中,栈中是什么根本无所谓
}
变体2——自己生成括号
思路变体:【回溯】 + 【左右括号计数】
这里利用了一个括号字符串的性质进行【剪枝】:当右括号数量超过左括号时,必然串无效——这个性质之后还会再派上大用场
▊【Q22】(md) 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:
n = 3
输出:[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]
class Solution {
/*
* 【回溯算法】
* 思路 :其实这是很典型的需要减枝的回溯算法,应该不难想到
*
* String tempString是暂存串
* int L, int R 记录左右括号的个数,是用于减枝的(右括号不可能多于左括号)
*
* 其实,剪枝的条件(右括号不可能多于左括号)也是再给出现一个有效串做铺垫:
* 如果出现left==right,则这串不一定有效
* 当限制了右括号不可能多于左括号时,如果出现left==right则一定是right追上了left,则这串一定有效
*
* 这就是【左右括号计数】解决括号匹配问题的思路————抛开栈的一个新思路
*/
public List<String> generateParenthesis(int n) {
traceBack(n, "", 0, 0);
return resList;
}
public List<String> resList = new ArrayList<>();
public void traceBack(int n, String tempString, int L, int R) {
if(R + L == 2*n) {
if( R == n && L == n) {
resList.add(tempString.toString());
return;
}else {
return;// 减枝
}
}
if(L < R) {
return;// 减枝
}
traceBack(n, tempString + "(", L+1, R);
traceBack(n, tempString + ")", L, R+1);
}
}
究极变体,由定性到定量——寻找最长有效括号的长度
我们将从【栈】【动态规划】【左右括号计数】三个角度去攻克这个问题
【Q32】(hd) 最长有效括号
给定一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长的包含有效括号的子串的长度。
示例 1:输入: “(()”
输出: 2
示例 2:
输入: “)()())”
输出: 4
示例 3:
输入: “()(())”
输出: 4
class Solution {
public int longestValidParentheses(String s) {
/*
* 【栈】
*
* 我们维护一个栈,值为下标
* 每次遇到'('时,毫不犹豫的将其下标入栈,等待被配对弹出;
* 每次遇到')'时,就执行一次弹出操作:
* 如果这时栈空了,说明没有'('能与其配对,它的下标入栈(除非遇到下一个无法配对的')',它将永远垫底)
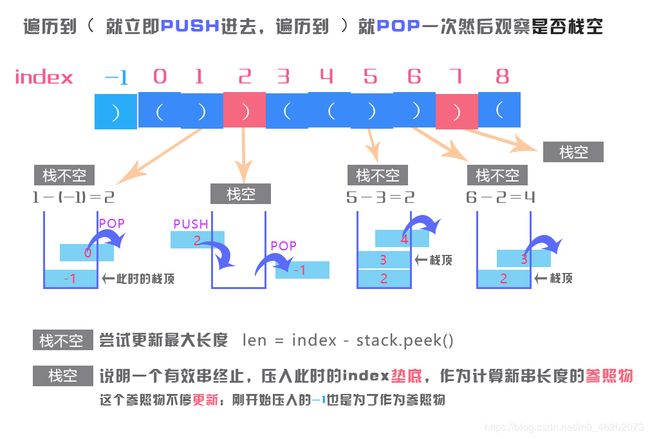
* 如果栈不空,则尝试更新maxLen,此时的有效括号长度为此时的小标,与弹出后此时的栈顶的下标之差
*
* 理解:
* 1.每次'('下标入栈,都是【等待被配对弹出】的;
* 每次')'下标入栈,都说明此时有效串断了,它的下标现在垫底用的,作为【新串开始的前一个字符位置】
* 2.一个重要的技巧:先入栈一个-1。这相当于在原串的最前面加了个')'———这不影响结果,而且解决了第一个字符为')'的情况下,pop出错的问题
* 3.解决【括号字符串】问题有一个看似奇怪但绝对安全的思路: ')'去配对它左边的第一个'(',然后消掉 ,准没错!!!!!
* 4.还是那个重要思路: ')'是有可能作为结束一个有效串的标志的
* 5.再理解一下-1吧!它是一个有效串结束的标志,作为参照下标,等价于多出的')'。当下一个')'将其顶替后,它的使命也就结束了
*/
Stack<Integer> stack = new Stack<>();
stack.add(-1);
int maxLen = 0;
for(int i = 0; i < s.length(); i++) {
if(s.charAt(i) == '(') {
stack.add(i);
}else {
stack.pop();
if(stack.isEmpty()) {
stack.add(i);
}else {
maxLen = Math.max(maxLen, i - stack.peek());
}
}
}
return maxLen;
}
}
class Solution {
/*
* 【动态规划】
*
* 举个例子帮助理解:
* 下标:0 1 2 3 4 5
* ( ) ( ( ) )
* dp: 0 2 0 0 2 6
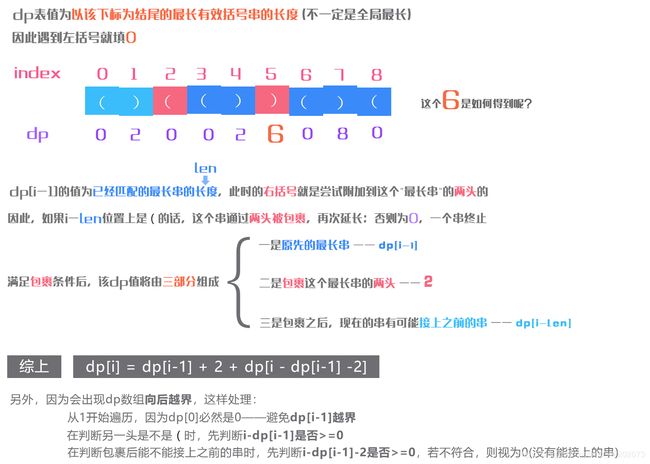
* dp表的值表示以当前括号做为结尾的最长有效括号长度————以'('结尾,必然填0,不用管; 以')'结尾,长度由三部分组成(★☆★):
*
* 以index=5处的')'为例:
* 先找到左边未被匹配的第一个'('。index=3处的'('已经是已经匹配的有效字符串的一部分,所以应该看这个有效字符串之前的第一个是否为'(',
* 即s.charAt(i - dp[i-1] - 1)是否为'('
* 如果是'('的话,则匹配上,原先的串被【加长】。因此第一部分是原先的串长dp[i-1];第二部分是刚刚匹配上从而加长的2
* 即如果此时的')'能和 i - dp[i-1] - 1 处的'('匹配上,则 dp[i] = dp[i - 1] + 2
* 千万别忘了,当这括号匹配上时(index=5,2),就有可能接上之前的有效串(在index=5,2匹配之前,index=3,4显然和index=0,1是独立的,但现在接上了)
* 即再尝试加上刚匹配上的'('之前1个位置的dp值,即再加上dp[i - dp[i-1] - 2]
*
* 三部分呼之欲出:dp[i] = dp[i - dp[i-1] - 2] + dp[i-1] + 2
* 但是:一来 i - dp[i-1] - 1 ,即有效串左边的第一个位置有可能不存在需要提前判断:i - dp[i-1] - 1 >= 0 && ...
* 二来 一次匹配后,在尝试接上再之前的有效串的时候,也可能不存在:i - dp[i-1] - 2 >= 0 ...
*
*/
public int longestValidParentheses(String s) {
int len = s.length();
int[] dp = new int[len];
int maxLen = 0;
for(int i = 1; i < len; i++) {
if(s.charAt(i) == ')') {
if(i - dp[i-1] - 1 >= 0 && s.charAt(i - dp[i-1] - 1) == '(') {
dp[i] = (i - dp[i-1] - 2 >= 0 ? dp[i - dp[i-1] - 2] : 0) + dp[i-1] + 2;
}
maxLen = Math.max(maxLen, dp[i]);
}
}
return maxLen;
}
}
class Solution {
/*
* 【括号计数】
*
* 之前在[回溯法生成有效括号]时,使用的就是这种思路:从左向右遍历,如果右括号')'的个数多于左括号'('的个数,那就没有继续的必要了
* 这与【')'和'('相消】的括号的性质是相契合的
*
* 我们从左向右遍历,是'('就left计数器加一,是')'就给right计数器加一
* 每次加一后都检查一遍:
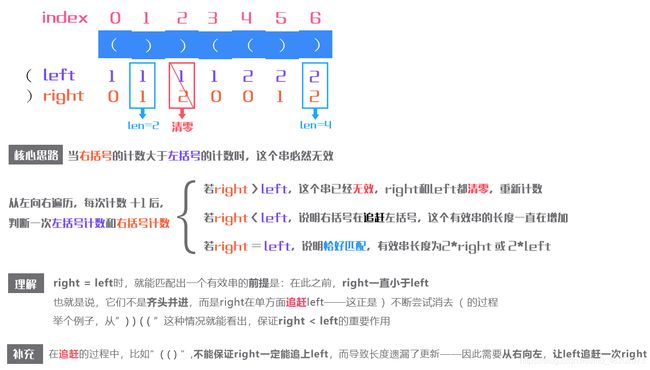
* 如果right > left,则这个串已经无效的,将计数器都置0重新开始
* 如果right < left,说明右括号在【追赶】左括号,这个有效串的长度一直在加长
* 如果right = left,说明恰好匹配,有效串长度为2*right 或 2*left
*
* 理解(!!!):
* 你可能会有疑问,当左右括号数量相等,就一定有效?很容易举出这样的反例啊:"))(("
* 其实,"数量相等"在计数时,当右括号多于左括号时,就清零一次,重新开始:
* "))(("的前两个括号,并没有计数,也不可能出现left==right的情况
*
* 这个"相等",并不是left和right齐头并进,而是right对left的单方面追赶————这就是')'尝试消去'('的过程
* 当right超过left,这段"赛跑"就结束了(这个有效串的长度终止了);需要让left先跑几步,right再去追它(需要先有若干'(',再让')'取匹配它)
*
* 还有一个致命的问题:当right一直没追上left时,就不会出现2*right 或 2*left的有效串长度更新,比如"(()"这种情况
* 如何解决呢?
* 从另一个方向开始跑,让left去追right————让'('去匹配')'
*
*
* 通过这样的"两个方向的追赶",也就保证得出了最终的正确答案
*/
public int longestValidParentheses(String s) {
int len = s.length();
int left = 0;
int right = 0;
int maxLen = 0;
for(int i = 0; i < len; i++) {
if(s.charAt(i) == '(') {
left++;
}else {
right++;
}
if(right == left) {
maxLen = Math.max(maxLen, 2 * right);
}else if(right > left) {
left = 0;
right = 0;
}
}
right = 0;
left = 0;
for(int i = len - 1; i >= 0; i--) {
if(s.charAt(i) == ')') {
right++;
}else {
left++;
}
if(left == right) {
maxLen = Math.max(maxLen, 2 * left);
}else if(left > right) {
right = 0;
left = 0;
}
}
return maxLen;
}
}
部分题目来源
【Leetcode Q20】有效的括号
【Leetcode Q22】括号生成
【Leetcode Q32】最长有效括号
End ♬ By a Lolicon