Python的实用机器学习--重要概念
文章目录
- 介绍
- 标量
- 向量
- 矩阵
- 张量
- 范数
- 本征分解
- 奇异值分解
- 随机变量
- 概率分布
- 概率质量函数
- 概率密度函数
- 边际概率
- 条件概率
- 贝叶斯定理
- 统计
- 数据挖掘
- 人工智能
- 自然语言处理
- 深度学习
- 人工神经网络
- 反向传播
- 多层感知器
- 卷积神经网络
- 递归神经网络
- 长短期内存网络
- 自动编码器
- 机器学习方法
介绍
我们将讨论应用数学中的一些关键术语和概念,即线性代数和概率论。
这些概念在机器学习中得到了广泛的应用,并形成了机器学习算法,模型和过程中的一些基本结构和原理。
标量
标量通常表示单个数字而不是数字的集合。一个简单的示例可能是x = 5或x∈R,其中x是指向单个数字或实值单个数字的标量元素。
向量
向量定义为一种结构,其中包含按顺序排列的数字数组。
这基本上意味着集合中数字的顺序或顺序很重要。向量在数学上可以表示为x = [x1,x2,...,xn],这基本上告诉我们x是一维向量,在数组中具有n个元素。可以使用确定其在向量中位置的数组索引来引用每个元素。以下代码段向我们展示了如何在Python中表示简单的向量。
In [1]: x = [1, 2, 3, 4, 5]
...: x
Out[1]: [1, 2, 3, 4, 5]
In [2]: import numpy as np
...: x = np.array([1, 2, 3, 4, 5])
...:
...: print(x)
...: print(type(x))
[1 2 3 4 5]
<class 'numpy.ndarray'>
因此,您可以看到Python列表以及基于numpy的数组都可以用来表示向量。数据集中的每一行都可以充当n个属性的一维向量,可以用作学习算法的输入。
矩阵
矩阵是一种二维结构,基本上可以容纳数字。通常也称为2D阵列。与向量相比,与单个向量索引相比,可以使用行和列索引来引用每个元素。
在数学上,您可以将矩阵描述为
M = [ m 11 m 12 m 13 m 21 m 22 m 23 m 31 m 32 m 33 ] M=\left[\begin{array}{lll}m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33}\end{array}\right] M=⎣⎡m11m21m31m12m22m32m13m23m33⎦⎤
,这样M是具有三行三列的3 x 3矩阵,每个元素都由mrc表示,r表示行索引,c表示列索引。
矩阵可以很容易地用Python表示为列表列表,我们可以利用numpy数组结构,如以下代码段所示。
In [3]: m = np.array([[1, 5, 2],
...: [4, 7, 4],
...: [2, 0, 9]])
In [4]: # view matrix
...: print(m)
[[1 5 2]
[4 7 4]
[2 0 9]]
In [5]: # view dimensions
...: print(m.shape)
(3, 3)
但是,您可以看到我们如何轻松地利用numpy数组来表示矩阵。
你可以将具有行和列的数据集视为矩阵,以便数据特征或属性由列表示,每行表示一个数据样本。
稍后我们将在分析中使用相同的类比。
当然,您可以执行矩阵运算,例如加,减,乘积,逆,转置,行列式等等。以下代码片段显示了一些流行的矩阵运算。
In [9]: # matrix transpose
...: print('Matrix Transpose:\n', m.transpose(), '\n')
...:
...: # matrix determinant
...: print ('Matrix Determinant:', np.linalg.det(m), '\n')
...:
...: # matrix inverse
...: m_inv = np.linalg.inv(m)
...: print ('Matrix inverse:\n', m_inv, '\n')
...:
...: # identity matrix (result of matrix x matrix_inverse)
...: iden_m =np.dot(m, m_inv)
...: iden_m = np.round(np.abs(iden_m), 0)
...: print ('Product of matrix and its inverse:\n', iden_m)
...: Matrix Transpose:
[[1 4 2]
[5 7 0]
[2 4 9]]
Matrix Determinant: -105.0
Matrix inverse:
[[-0.6 0.42857143 -0.05714286]
[ 0.26666667 -0.04761905 -0.03809524]
[ 0.13333333 -0.0952381 0.12380952]]
Product of matrix and its inverse:
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
张量
你可以将张量视为通用数组。
张量基本上是具有可变数量的轴的数组。
三维张量T中的元素可以用 T x , y , z T_{x, y, z} Tx,y,z表示,其中x,y,z表示用于指定元素T的三个轴。
范数
范数是用于计算向量大小的度量,通常也定义为从原点到向量表示的点的距离的度量。在数学上,向量的pth范数表示如下。
L p = ∥ x p ∥ = ( ∑ i ∣ x i ∣ p ) 1 p L^{p}=\left\|x_{p}\right\|=\left(\sum_{i}\left|x_{i}\right|^{p}\right)^{\frac{1}{p}} Lp=∥xp∥=(∑i∣xi∣p)p1
使得p≥1和p∈R。机器学习中流行的规范包括在Lasso回归模型中广泛使用的 L 1 L^{1} L1规范和在岭回归模型中使用的 L 2 L^{2} L2规范(也称为欧几里得规范)。
本征分解
这基本上是一个矩阵分解过程,因此我们可以将矩阵分解或分解为一组特征向量和特征值。
矩阵的本征分解可以用数学公式 M = V diag ( λ ) V − 1 M=V \operatorname{diag}(\lambda) V^{-1} M=Vdiag(λ)V−1表示,这样矩阵M总共有n个线性独立的本征向量,分别表示为
{ v ( 1 ) , v ( 2 ) , … , v ( n ) } \left\{v^{(1)}, v^{(2)}, \ldots, v^{(n)}\right\} {v(1),v(2),…,v(n)}
及其对应的特征值可以表示为
{ λ 1 , λ 2 , … , λ n } \left\{\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}\right\} {λ1,λ2,…,λn}。
矩阵V由矩阵的每一列组成一个特征向量,即 V = [ v ( 1 ) , v ( 2 ) , … , v ( n ) ] V=\left[v^{(1)}, v^{(2)}, \ldots, v^{(n)}\right] V=[v(1),v(2),…,v(n)],
向量λ包含所有特征值,即
λ = [ λ 1 , λ 2 , … , λ n ] \lambda=\left[\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}\right] λ=[λ1,λ2,…,λn]。
矩阵的特征向量被定义为非零向量,以使得在将矩阵乘以特征向量后,结果仅改变特征向量本身的比例,即:结果是标量乘以特征向量。
该标量被称为对应于特征向量的特征值。
从数学上讲,可以用Mv =λv表示,其中M是我们的矩阵,v是特征向量,而λ是相应的特征值。
以下Python代码段描述了如何从矩阵中提取特征值和特征向量。
In [4]: # eigendecomposition
...: m = np.array([[1, 5, 2],
...: [4, 7, 4],
...: [2, 0, 9]])
...:
...: eigen_vals, eigen_vecs = np.linalg.eig(m)
...:
...: print('Eigen Values:', eigen_vals, '\n')
...: print('Eigen Vectors:\n', eigen_vecs)
...:
Eigen Values: [ -1.32455532 11.32455532 7. ]
Eigen Vectors:
[[-0.91761521 0.46120352 -0.46829291]
[ 0.35550789 0.79362022 -0.74926865]
[ 0.17775394 0.39681011 0.46829291]]
奇异值分解
奇异值分解过程(也称为SVD)是另一个矩阵分解或分解过程,因此我们能够分解矩阵以获得奇异向量和奇异值。即使本征分解在某些情况下可能不适用,任何实矩阵都将始终被SVD分解。在数学上,SVD可以定义如下。考虑具有尺寸m x n的矩阵M,使得m表示总行,n表示总列,则矩阵的SVD可用下式表示
M m × n = U m × m S m × n V n × n T M_{m \times n}=U_{m \times m} S_{m \times n} V_{n \times n}^{T} Mm×n=Um×mSm×nVn×nT
这为我们提供了分解方程式的以下主要组成部分。
U m × m U_{m \times m} Um×m是一个m x m ary矩阵,其中每列代表一个左奇异矢量
S m × n S_{m \times n} Sm×n是对角线上带有正数的m x n矩阵,也可以表示为奇异值的向量
V n × n T V_{n \times n}^{T} Vn×nT是n x n 单一矩阵,其中每一行代表一个右奇异向量
在某些表示中,行和列可以互换,但最终结果应该相同,即,U和V始终正交。以下代码段显示了Python中的简单SVD分解。
In [7]: # SVD
...: m = np.array([[1, 5, 2],
...: [4, 7, 4],
...: [2, 0, 9]])
...:
...: U, S, VT = np.linalg.svd(m)
...:
...: print('Getting SVD outputs:-\n')
...: print('U:\n', U, '\n')
...: print('S:\n', S, '\n')
...: print('VT:\n', VT, '\n')
...:
Getting SVD outputs:-
U:
[[ 0.3831556 -0.39279153 0.83600634]
[ 0.68811254 -0.48239977 -0.54202545]
[ 0.61619228 0.78294653 0.0854506 ]]
S:
[ 12.10668383 6.91783499 1.25370079]
VT:
[[ 0.36079164 0.55610321 0.74871798]
[-0.10935467 -0.7720271 0.62611158]
[-0.92621323 0.30777163 0.21772844]]
SVD作为一种技术,尤其是奇异值,在基于摘要的算法和诸如降维的各种其他方法中非常有用。
随机变量
随机变量是概率和不确定性度量中经常使用的变量,基本上是可以随机采用各种值的变量。这些变量通常可以是离散或连续的类型。
概率分布
概率分布是一种分布或排列,用于描述一个或多个随机变量采用其每个可能状态的可能性。基于变量的离散或连续变量通常有两种主要分布。
概率质量函数
概率质量函数,也称为PMF,是离散随机变量的概率分布。流行的例子包括泊松分布和二项式分布。
概率密度函数
概率密度函数,也称为PDF,是连续随机变量的概率分布。流行的例子包括正态分布,均匀分布和学生的T分布。
边际概率
当我们已经具有一组随机变量的概率分布并且我们要计算这些随机变量的子集的概率分布时,将使用边际概率规则。对于离散随机变量,我们可以如下定义边际概率。
P ( x ) = ∑ y P ( x , y ) P(x)=\sum_{y} P(x, y) P(x)=∑yP(x,y)
对于连续随机变量,我们可以使用以下积分操作对其进行定义。
p ( x ) = ∫ p ( x , y ) d y p(x)=\int p(x, y) d y p(x)=∫p(x,y)dy
条件概率
当我们要确定某个事件将要发生的概率,例如另一个事件已经发生时,将使用条件概率规则。数学上表示如下。
P ( x ∣ y ) = P ( x , y ) P ( y ) P(x \mid y)=\frac{P(x, y)}{P(y)} P(x∣y)=P(y)P(x,y)
假设y已经发生,这告诉我们x的条件概率。
贝叶斯定理
这是另一个规则或定理,当我们知道关注事件P(A)的概率,基于我们关注事件P(BA)的另一事件的条件概率并且我们想要确定考虑到其他事件,我们关注的事件发生在P(AB)。
可以使用以下表达式在数学上进行定义。
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
这里A和B是事件, P ( B ) = ∑ x P ( B ∣ A ) P ( A ) P(B)=\sum_{x} P(B \mid A) P(A) P(B)=∑xP(B∣A)P(A)
统计
统计学领域可以定义为一个专门的数学分支,它由收集,组织,分析,解释和呈现数据的框架和方法组成。
通常,这更多地属于应用数学范畴,并且借鉴了线性代数,分布,概率论和推论方法的概念。
统计学中有两个主要领域,如下所述:
•描述性统计学
•推断性统计学
任何统计过程的核心组成部分都是数据。
因此,通常通常首先进行数据收集,这可能是全局性的,由于各种约束通常被称为样本,因此通常称为总体或受更严格限制的子集。
通常从调查,实验,数据存储和观察研究中手动收集样本。
根据这些数据,使用统计方法进行各种分析。
使用描述性统计信息来了解使用各种数据的数据的基本特征 汇总和汇总措施可以更好地描述和理解数据。
这些可以是标准度量,例如均值,中位数,众数,偏度,峰度,标准差,方差等。 如果你有兴趣,可以参考任何一本有关统计的标准书来深入研究这些度量。
下面的代码段描述了如何计算一些基本的描述性统计量。
In [74]: # descriptive statistics
...: import scipy as sp
...: import numpy as np
...:
...: # get data
...: nums = np.random.randint(1,20, size=(1,15))[0]
...: print('Data: ', nums)
...:
...: # get descriptive stats
...: print ('Mean:', sp.mean(nums))
...: print ('Median:', sp.median(nums))
...: print ('Mode:', sp.stats.mode(nums))
...: print ('Standard Deviation:', sp.std(nums))
...: print ('Variance:', sp.var(nums))
...: print ('Skew:', sp.stats.skew(nums))
...: print ('Kurtosis:', sp.stats.kurtosis(nums))
...:
Data:[ 2 198 10 17 13 189 19 164 14 16 155]
Mean: 12.3333333333
Median: 14.0
Mode: ModeResult(mode=array([16]), count=array([2]))
Standard Deviation: 5.44875113112
Variance: 29.6888888889
Skew: -0.49820055879944575
Kurtosis: -1.0714842769550714
像pandas,scipy和numpy这样的库和框架通常可以帮助我们在Python中轻松地计算描述性统计数据并汇总数据。当我们要检验假设,得出推断以及关于数据样本或总体特征的结论时,将使用推断统计。假设检验,相关性和回归分析,预测和预测之类的框架和技术通常用于任何形式的推断统计。
数据挖掘
数据挖掘领域涉及从非平凡的数据集中发现和提取模式,知识,见解和有价值的信息的过程,方法,工具和技术。当数据集通常可以从数据库和数据仓库中获得时,它们被认为是非常重要的。
数据挖掘本身是一个多学科领域,融合了数学,统计学,计算机科学,数据库,机器学习和数据科学等概念和技术。
一般而言,该术语用词不当,因为“挖掘”是指从数据而非数据本身中挖掘实际见解或信息!在KDD或数据库中的知识发现的整个过程中,数据挖掘是进行所有分析的步骤。
通常,KDD和数据挖掘都与机器学习密切相关,因为它们都与分析数据有关以提取数据。有用的模式和见解。
因此,方法论,概念,技术, 并且过程在它们之间共享。 行业中遵循的数据挖掘的标准过程称为CRISP-DM模型。
人工智能
人工智能领域包含多个子领域,包括机器学习,自然语言处理,数据挖掘等。可以将其定义为制作智能代理,机器和程序的艺术,科学和工程。
该领域旨在为一个简单而又极其艰巨的目标提供解决方案:“机器可以像人类一样思考,推理和行动吗?”
实际上,人工智能早在1300年代就存在了,当时人们开始提出这样的问题,并开始研究可用于概念而不是像计算器这样的数字的建筑工具。
随着Alan Turing,McCullouch和Pitts人工神经元的发现和发明,人工智能的发展稳步发展。直到1980年代,由于专家系统的成功,人工智能的复兴,霍普菲尔德(Hopfield),鲁梅尔哈特(Rumelhart),麦克莱兰德(McClelland),欣顿(Hinton)等神经网络的兴起,人工智能得以再次复兴。
得益于更快,更好的计算 摩尔定律导致诸如数据挖掘,机器学习乃至深度学习之类的领域应运而生,以解决复杂的问题,而使用传统方法无法解决这些问题。
AI的一些主要目标包括认知功能的仿真,也称为认知学习,语义和知识表示,学习,推理,问题解决,计划和自然语言处理。 AI借鉴了统计学习,应用数学,优化方法,逻辑,概率论,机器学习,数据挖掘,模式识别和语言学的工具,概念和技术。人工智能仍在随着时间的推移而发展,并且在这一领域正在进行许多创新,包括一些最新的发现和发明,例如自动驾驶汽车,聊天机器人,无人机和智能机器人。
自然语言处理
自然语言处理(NLP)领域是一个多学科领域,结合了计算语言学,计算机科学和人工智能的概念。 NLP涉及使机器处理,理解自然语言并与之交互的能力。使用NLP构建的应用程序或系统的主要目标是使机器和随时间演变的自然语言之间实现交互。这方面的主要挑战包括知识和语义表示,自然语言理解,生成和处理。 NLP的一些主要应用如下。
•机器翻译
•语音识别
•问答系统
•上下文识别和解析
•文本摘要
•文本分类
•信息提取
•情感和情感分析
•主题细分
使用NLP和文本分析中的技术,您可以处理文本数据以处理,注释,分类,聚类,汇总,提取语义,确定情感等等!
下面的示例代码片段描述了对文本数据的一些基本NLP操作,其中,我们根据文档的构成文法为文档(文本句子)添加了各种组件,例如语音部分,短语级别标签等。
from nltk.parse.stanford import StanfordParser
sentence = 'The quick brown fox jumps over the lazy dog'
# create parser object
scp = StanfordParser(path_to_jar='E:/stanford/stanford-parser-full-2015-04-20/stanford-parser.jar',path_to_models_jar='E:/stanford/stanford-parser-full-2015-04-20/stanford-parser-3.5.2-models.jar')
# get parse
treeresult = list(scp.raw_parse(sentence))
tree = result[0]
In [98]: # print the constituency parse tree
...: print(tree)
(ROOT
(NP
(NP (DT The) (JJ quick) (JJ brown) (NN fox))
(NP
(NP (NNS jumps))
(PP (IN over) (NP (DT the) (JJ lazy) (NN dog))))))
In [99]: # visualize constituency parse tree
...: tree.draw()
深度学习
如前所述,深度学习领域是机器学习的一个子领域,最近受到了广泛的关注。
其主要目标是使机器学习研究更接近其“使机器变得智能”的真正目标。
深度学习通常被称为神经网络的品牌重塑。
在某种程度上是正确的,但深度学习肯定不仅限于基本的神经网络。
基于深度学习的算法涉及使用来自表示学习的概念,其中在不同层中学习了数据的各种表示,这也有助于从数据中自动提取特征。
简单来说,基于深度学习的方法试图通过将数据表示为概念的分层层次结构来构建机器智能,其中概念的每一层都是从其他较简单的层构建的。
这种分层架构本身是任何深度学习算法的核心组件之一。
通过学习技术,我们基本上尝试学习数据样本和输出之间的映射,然后尝试预测较新数据样本的输出。
代表性学习除了学习从输入到输出的映射之外,还试图理解数据本身中的表示。
与常规技术相比,这使得深度学习算法极其强大,而常规技术则需要特征提取和工程等领域的大量专业知识。 与旧的机器学习算法相比,深度学习在性能和可扩展性方面都非常有效,数据越来越多。
的确,正如吴恩达(Andrew Ng)正确指出的那样,在过去十年中,我们注意到了与深度学习相关的一些明显趋势和特征。
它们的概述如下:
•深度学习算法基于分布式表示学习,并且随着时间的推移,它们会随着更多数据的出现而开始表现更好。
•深度学习可以说是神经网络的重塑,但与之相比,它有很多东西传统的神经网络。
•更好的软件框架(如tensorflow,theano,caffe,mxnet和keras),再加上卓越的硬件,使得构建极其复杂的,多层的,具有巨大规模的深度学习模型成为可能。到自动特征提取以及执行有监督的学习操作,这些已帮助数据科学家和工程师解决了随着时间推移而日益复杂的问题。
以下几点描述了大多数深度学习的显着特征 算法,本书中将使用其中的一些算法。
•概念的分层表示。 这些概念在机器学习术语(数据属性)中也称为功能。
•数据的分布式表示性学习是通过多层体系结构(无监督学习)进行的。
•更复杂,更高级的功能和概念源自更简单,更简单的概念。 级功能。
•通常认为“深度”神经网络除输入和输出层外还至少具有一个以上的隐藏层。通常,它至少由三到四个隐藏层组成。
•深层体系结构具有多层体系结构,其中每一层都包含多个非线性处理单元。每层的输入是体系结构中的上一层。通常,第一层是输入,最后一层是输出。
•可以执行自动特征提取,分类,异常检测和许多其他机器学习任务。这将使您对与深度学习有关的概念有一个良好的基础掌握。
人工神经网络
人工神经网络(ANN)是一种计算模型和体系结构,可模拟生物神经元及其在大脑中的功能。
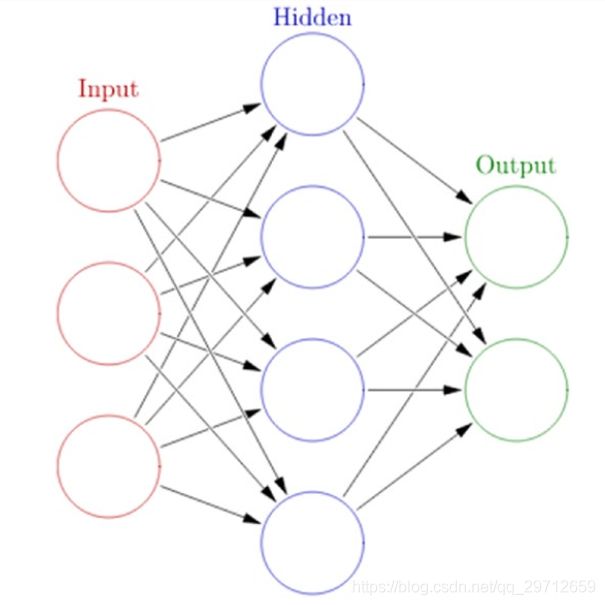
通常,ANN具有互连的节点层。节点及其相互连接类似于我们大脑中的神经元网络。典型的ANN具有输入层,输出层以及在输入和输出之间具有互连的至少一个隐藏层,
如图1,
任何基本ANN始终将具有多层节点,特定的连接模式和链接节点/神经元的层,连接权重和激活函数之间的关系,将加权的输入转换为输出。网络的学习过程通常涉及成本函数,目标是优化成本函数(通常将成本最小化)。权重在学习过程中不断更新
反向传播
反向传播算法是一种用于训练ANN的流行技术,它导致了1980年代神经网络的流行重新出现。该算法通常有两个主要阶段-传播和权重更新。
简要描述如下:
1、传播
a、输入数据样本向量通过神经网络向前传播,以从输出层生成输出值。
b、将生成的输出向量与该输入数据向量的实际/期望输出向量进行比较。
c、计算输出单位的误差差
d、反向传播误差值以在每个节点/神经元处生成增量
2、体重更新
a、通过将输出增量(误差)与输入激活量相乘来计算重量梯度。
b、使用学习率来确定要从原始权重中减去的梯度百分比并更新节点的权重。
将这两个阶段重复多次,并进行多次迭代/时期,直到获得满意的结果。 通常将反向传播与优化算法或函数(例如随机梯度下降)一起使用
多层感知器
多层感知器(也称为MLP)是具有至少三层(输入,输出和至少一层)的完全连接的前馈人工神经网络。 隐藏层),其中每个层都完全连接到相邻层。
每个神经元通常是一个非线性功能处理单元。 反向传播通常用于训练MLP,当深度神经网络具有多个隐藏层时,它们甚至是MLP。
卷积神经网络
卷积神经网络,也称为卷积神经网络或CNN,是人工神经网络的一种变体,专门用于模拟视觉皮层的功能和行为。 CNN通常由以下三个组件组成。
•多个卷积层,由多个卷积的滤波器组成 通过基本计算点积以给出二维激活图,从而在输入数据的高度和宽度(例如,图像原始像素)上绘制图像。 将所有地图叠加在所有过滤器上后,我们最终从卷积层获得了最终输出。
•池化层,基本上是执行非线性下采样的层,以减少卷积层输出的输入大小和参数数量,从而进一步推广模型,防止过度拟合并减少计算时间。筛选器会遍历输入的高度和宽度,并通过求和,求平均值或最大值之类的总和来减少输入。典型的合并组件是平均或最大合并。
•完全连接的MLP执行图像分类和对象识别之类的任务。
递归神经网络
递归神经网络,也称为RNN,是一种特殊类型的人工神经网络,通过使用一种特殊类型的循环体系结构,可以基于过去的知识来保留信息。
它们在与数据相关的领域中经常使用,这些领域的序列类似于预测句子的下一个单词。这些循环网络被称为循环网络,因为它们对输入数据序列中的每个元素执行相同的操作和计算。 RNN具有有助于从过去序列中捕获信息的内存。
Colah的博客http://colah.github.io/posts/2015-08-Understanding-LSTMs/显示了RNN的典型结构以及如何根据输入序列展开网络来工作。
长短期内存网络
RNN擅长处理基于序列的数据,但是随着序列开始增加,它们会随着时间的流逝而逐渐失去历史上下文,因此输出并不总是需要的。这就是长短期存储网络(俗称LSTM)出现的地方! LSTM由Hochreiter&Schmidhuber于1997年引入,可以记住基于长序列的数据中的信息,并可以防止梯度消失等问题,这种问题通常发生在经过反向传播训练的ANN中。 LSTM通常包括三个或四个门,包括输入,输出和一个特殊的忘记门。
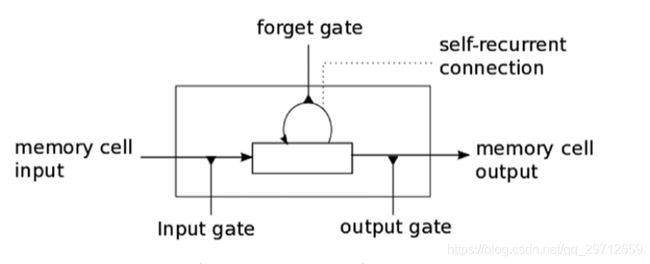
输入门通常可以允许或拒绝进入的信号或输入以更改存储单元状态。输出门通常会根据需要将该值传播到其他神经元。遗忘门控制存储单元的自循环连接,以根据需要记住或忘记以前的状态。
通常,任何深度学习网络中都会堆叠多个LSTM单元,以解决诸如序列预测之类的现实问题。
自动编码器
自动编码器是一种专用的人工神经网络,主要用于执行无监督的机器学习任务。它的主要目的是学习数据表示,近似和编码。自动编码器可用于构建生成模型,执行降维和检测异常。
机器学习方法
机器学习具有多种算法,技术和方法论,可用于构建模型以使用数据解决实际问题。通常,可以在多个保护伞下以多种方式对相同的机器学习方法进行分类。以下是机器学习方法的一些主要广泛领域
1.基于学习过程中人为监督量的方法
a、监督学习
b、无监督学习
c、半监督学习。强化学习
2、基于从增量数据样本中学习的能力的方法
a、批量学习
b、在线学习
3、基于其从数据样本进行归纳的方法
a、基于实例的学习
b、基于模型的学习
应在哪种情况下使用哪种方法是一个十分困难的问题。