Reed Solomon编码

参考文章：https://blog.csdn.net/shelldon/article/details/54144730

参考文章：https://blog.csdn.net/shelldon/article/details/54729687

Reed Solomon利用范特蒙矩阵或者柯西矩阵的特性来实现纠错码的功能。下面着重介绍Reed Solomon编解码原理：

一、Reed Solomon编码

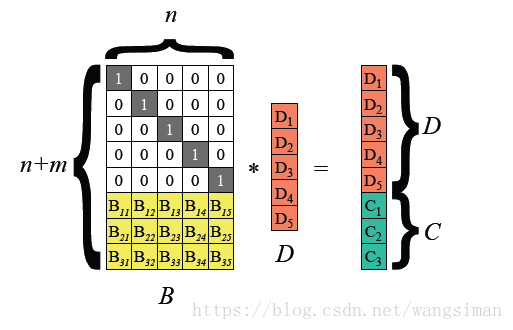
把输入数据视为向量D=(D1，D2，..., Dn）, 编码后数据视为向量（D1, D2,..., Dn, C1, C2,.., Cm)，RS编码可视为如下图所示矩阵运算。

编码矩阵B必须具有任意子矩阵可逆的特性。

二、Reed Solomon解码

RS最多能容忍m个数据块被删除，m包括实际数据和冗余数据。 数据恢复的过程如下：

（1）假设D1、D4、C2丢失，从编码矩阵中删掉丢失的数据块/编码块对应的行。 

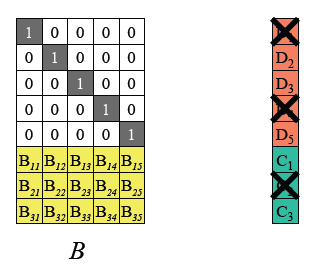
根据图1所示RS编码运算等式，可以得到如下B' 以及等式。

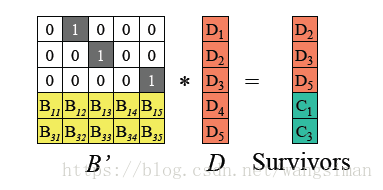
（2）由于B' 是可逆的，记B'的逆矩阵为 (B'^-1)，则B' * (B'^-1) = I 单位矩阵。两边左乘B' 逆矩阵。

（3）得到如下原始数据D的计算公式

三、有限域

假设每一个向量元素由8比特组成，那么矩阵相乘后的结果必然要超过8比特的范围，为了解决这个问题，我们引入有限域的概念。

1、域

一组元素的集合，以及在集合上的四则运算，构成一个域。其中加法和乘法必须满足交换、结合和分配的规律。加法和乘法具有封闭性，即加法和乘法结果仍然是域中的元素。   

域中必须有加法单位元和乘法单位元，且每一个元素都有对应的加法逆元和乘法逆元。但不要求域中的  0 有乘法逆元。   

2、有限域

有限域又称为伽罗华域，其仅含有限多个元素的域。 GF（2^w）表示含有2^w个元素的有限域。那么在计算机中常用的有限域是GF（2^8）

3、单位元
    Identity Element，也叫幺元（么元），通常使用e来表示单位元。单位元和其他元素结合时，并不会改变那些元素。
对于二元运算*，若a*e=a，e称为右单位元；若e*a=a，e称为左单位元，若a*e=e*a=a，则e称为单位元。

4、逆元
    对于二元运算*，若a*b=e，则a称为b的左逆元素，b称为a的右逆元素。若a*b=b*a=e，则称a为b的逆元，b为a的逆元。

5、本原多项式

    域中不可约多项式是不能够进行因子分解的多项式， 本原多项式 （primitive polynomial）是一种特殊的不可约多项式。当一个域上的本原多项式确定了，这个域上的运算也就确定了。本原多项式一般通过查表可得，同一个域往往有多个本原多项式。  通过将域中的元素化为多项式形式，可以将域上的乘法运算转化为普通的多项式乘法再模本原多项式。

    在计算机中有限域GF（2^8）常用的本原多项式是x^8+x^4+x^3+x^2+1。

6、多项式运算

对于GF（2^w）上的多项式计算，多项式系数只能取 0或1。所以加法等同于异或运算，减法等同于加法。

四、本原多项式

我们可以通过本原多项式生成一个有限域的所有元素，生成步骤如下：

设P(x)是GF（2^w）上的某一个本原多项式，GF（2^w）的元素产生步骤是： 
(1)给定一个初始集合，包含0,1和元素x，即  { 0,1,x}； 
(2)将这个集合中的最后一个元素，即x，乘以x，如果结果的度大于等于w，则将结果mod P(x)后加入集合；
(3)直到集合有2^w个元素，此时最后一个元素乘以x再mod P(x)的值等于1。

例如，GF(2^4)含有16个元素，本原多项式为P(x)=x^4+x+1，除了  0 、1外，另外14个符号均由本原多项式生成。

注意到x^14=x^3+1，此时计算x^15=x^14*x=(x^3+1)*x=x^4+x=1，生成结束。

生成元素	多项式表示	二进制表示	数值表示	推导过程
0	0	0000	0
x^0	x^0	0001	1
x^1	x^1	0010	2
x^2	x^2	0100	4
x^3	x^3	1000	8
x^4	x+1	0011	3	x^3*x = x^4 mod P(x) = x+1
x^5	x^2+x	0110	6	x^4*x = (x+1)*x = x^2+x
x^6	x^3+x^2	1100	12
x^7	x^3+x+1	1011	11	x^6*x = (x^3+x^2)*x = x^4 +x^3 mod P(x) = x^3+x+1
x^8	x^2+1	0101	5
x^9	x^3+x	1010	10
x^10	x^2+x+1	0111	7	x^9*x=(x^3+x)*x = x^4+x^2 mod P(x) = x^2+x+1
x^11	x^3+x^2+x	1110	14
x^12	x^3+x^2+x+1	1111	15	x^11*x=(x^3+x^2+x)*x = x^4+x^3+x^2 mod P(x) = x^3+x^2+x+1
x^13	x^3+x^2+1	1101	13	x^12*x=(x^3+x^2+1  )*x = x^4+x^3+x mod P(x)= x^3+1
x^14	x^3+1	1001	9	x^13*x=(x^3+x^2+1)*x = x^4+x^3+x mod P(x) = x^3+1
x^15	1	0001	1	x^14*x = (x^3+1)*x = x^4+x mod P(x) = 1

五、查表法

根据上述生成有限域的原理，我们也可以看出有限域中的乘法规则

x^7*x^9 = （x^3+x+1）*（x^3+x）mod P(x) 

这种多项式相乘和取模运算量是很大的。

由于指数运算是满足定理 ：假设a=g^n，b=g^m。那么a*b = g^n* g^m = g^(n+m)。所以我们可以根据a和b，分别查表得到n和m，然后查表g^(n+m)即可。这就叫做查表法。它可以快速的提升矩阵相乘的运算速度。

根据上文的GF(2^4)的元素表示，生成gflog表和gfilog表如下：

 

在GF(2^4)域上的乘法和除法，可以通过查表法得到

乘法：

    7 * 9 = gfilog[gflog[7] + gflog[9]] = gfilog[10 + 14]

       = gfilog[24 mod 15] = gfilog[9] = 10

除法：

    13 / 11 = gfilog[gflog[13] - gflog[11]] =  gfilog[13 - 7] = gfilog[6] = 12