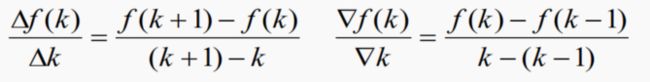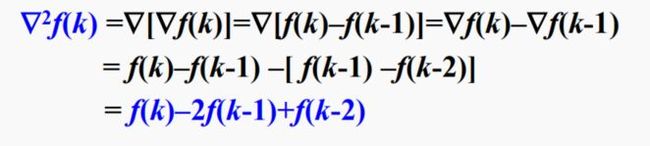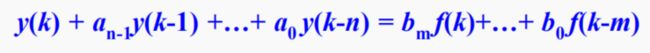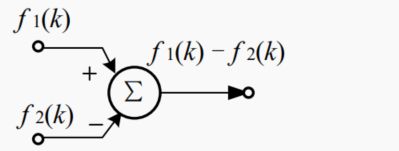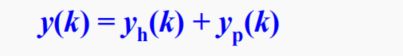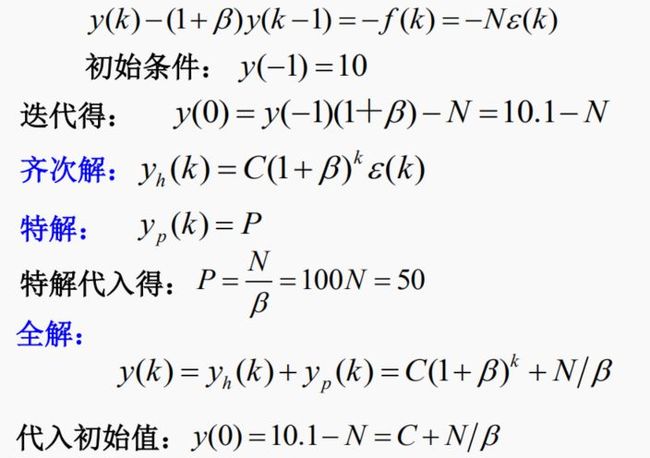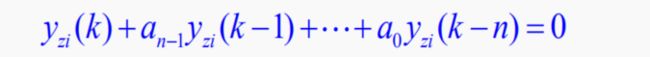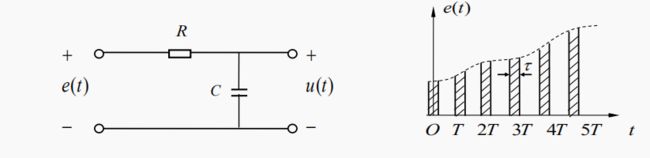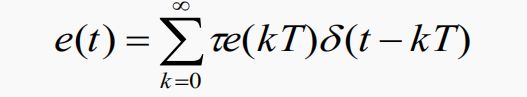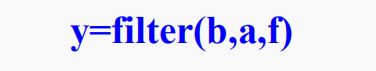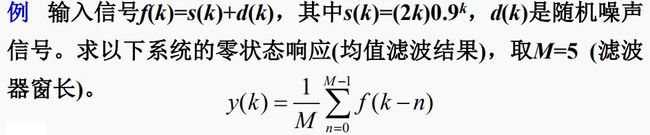信号与系统——差分方程的建立及经典解法
离散系统的解析描述--建立差分方程
1. 差分的定义
移位序列:设有序列f(k), 则… , f(k+2), f(k+1), f(k-1),f(k-2),… 等称为f(k)的移位序列。
差分运算:
一阶前向差分定义:
一阶后向差分定义:
我们主要用后向差分,简称为差分
差分的线性性质:
二阶差分定义:
m阶差分:
2. 差分方程
差分方程:由未知输出序列项与输入序列项构成的方程。
差分方程的一般形式:
方程的阶数:未知变量最高序号与最低序号的差。
由n阶差分方程描述的系统称为n阶系统。
描述LTI离散系统的是线性常系数差分方程
差分方程的模拟框图
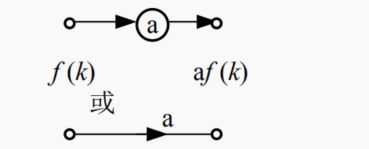
1.基本部件单元
数乘器
加法器
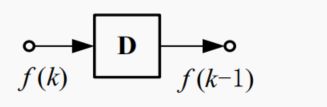
迟延单元(移位器)
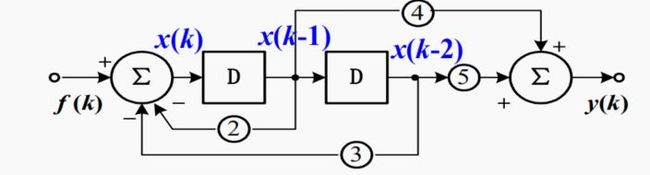
2. 由框图建立差分方程
例 已知框图,写出系统的差分方程
差分方程的经典解法
1.递推迭代
差分方程本质上是递推的代数方程,若已知初始条件和激励,利用迭代法可求得其数值解
注:迭代法一般不易得到解析形式的(闭合)解。
2.经典法
与连续系统的微分方程经典解类似,差分方程的解由齐次解yh(k)和特解yp(k)两部分组成,即
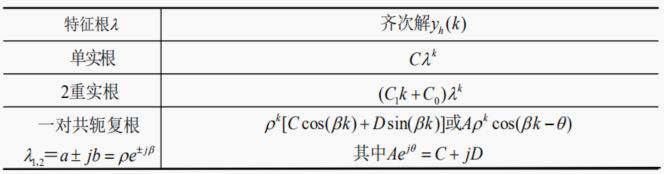
齐次解是对应齐次差分方程的解:
由特征根可以设定齐次解的函数形式。
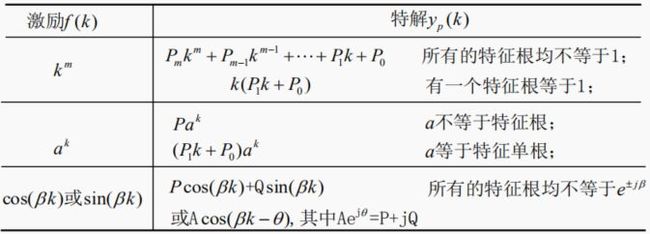
特解的函数形式与激励的函数形式有关。
3.齐次解的常用函数形式
4.特解的常用函数形式
说明:差分方程的齐次解也称为系统的自由响应,特解也称为强迫响应。本例中由于|λ|>1,故自由响应随k的增大而增大。
解:(1) 列出y(k)的差分方程
零输入响应的定义和求解
1.零输入响应的定义
零输入响应:离散系统的激励为零,仅由系统的初始状态引起的响应,用yzi(k)表示。
2.初始值的确定
3.求解步骤
(1)求特征方程的特征根;
(2)设定齐次解;
(3)直接代入初始状态 yzi(-l), l = 0, 1, … n-1, 求待定系数
零状态响应的定义和求解
1.零状态响应的定义
零状态响应:系统的初始状态yzs(-l)=0, l =1, 2, … n,为零,仅由激励 f(k)引起的响应,用yzs (k)表示。
2.初始值的确定
由迭代法求出初始值yzs(j), j= 0, 1, …n-1
3.求解步骤
(1)设定齐次解;
(2)设定特解,代入方程求解;
(3)代入初始值,求待定系数
斐波那契(Fibonacci)数列问题
假设每对大兔子每个月生一对小兔子,而每对小兔子一个月后长成大兔子,而且不会死亡。在最初一个月内有一对大兔子,问第n个月时一共有几对兔子.
解:每一个月中兔子的对数就构成了一个离散的时间信号。列出描述该问题的差分方程。
设y(k)为第k个月兔子对的数量。
第k个月兔子无论大小,在第k+1个月都会成为大兔子,从而在第k+2 个月中生出y(k)个小兔子
第k个月兔子无论大小,在第k+1个月都会成为大兔子,从而在第k+2 个月中生出y(k)个小兔子
而第k+2月中兔子的总个数y(k+2)等于大兔子对数y(k+1)与小兔子对的数量y(k)之和;
y(k+2)=y(k+1)+y(k)
这就是斐波那契数列问题的差分方程,即:
y(k+2)-y(k+1)-y(k)=0
简单空运控制系统
一个空运控制系统,它用一台计算机每隔一秒钟计算一次某飞机应有的高度x(k),另外用一雷达同时对此飞机实测一次高度y(k),把应有高度x(k)与一秒钟前的实测高度y(k-1)相比较得一差值,飞机的高度将根据此差值为正或为负来改变。试建立该问题的差分方程。
解:从第k-1秒到第 k秒这1秒钟内飞机升高为
K[x(k) - y(k -1)] = y(k) - y(k -1)
整理得:
y(k) +(K -1)y(k -1) = Kx(k)
RC取样输入和输出关系
一个RC电路如左图所示,输入端加取样电压信号e(t),如右图所示。试写出此系统每隔时间T输出电压u(k)与输入信号间关系的差分方程。
解:取样信号e(t)表示为如下冲激序列之和
上式即为描述输出离散电压与输入取样电压间关系的差分方程。
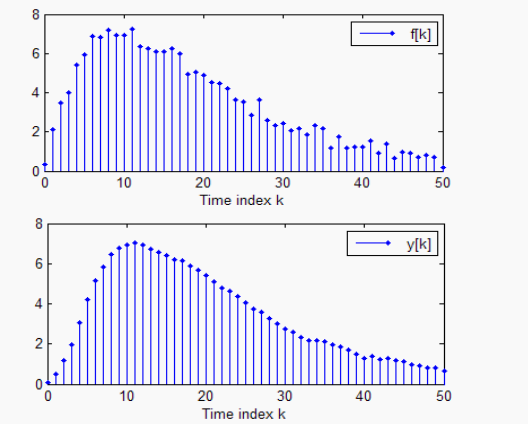
Matlab求解离散系统的零状态响应
在零状态时,MATLAB工具箱提供了一个filter函数,计算由差分方程描述的系统响应,其调用格式为
其中b=[b0,b1,b2,…, bm],a=[a0,a1,a2,…, an]分别是差分方程左右的系数向量,f表示输入序列,y表示系统的零状态响应。注意输出和输入序列的长度相同。
解:
R=51; %输入信号长度
d=rand(1,R)-0.5; %产生离散随机数
k=0:R-1;
s=2*k.*(0.9.^k);
f=s+d;
figure(1);stem(k,f,‘.’); %显示加噪信号
M=5;b=ones(M,1)/M; % f 前系数均为1/M
a=1;
y=filter(b,a,f); %求零状态响应
figure(2);
stem(k,y,‘.’); %显示平滑滤波结果
NUM448
![]()
个人博客式公众号
![]()
用心每一天
![]()