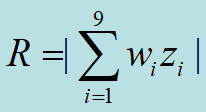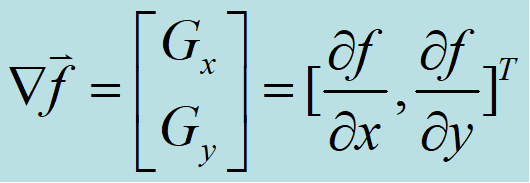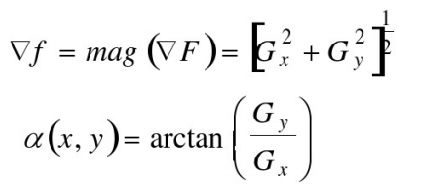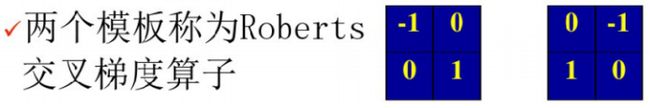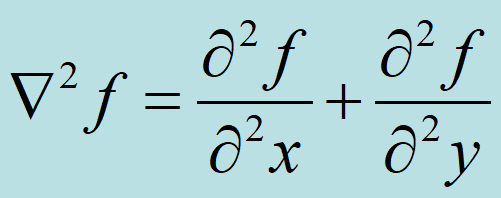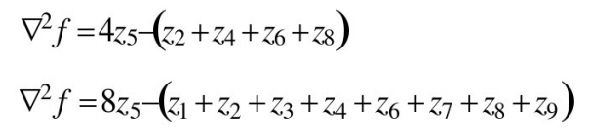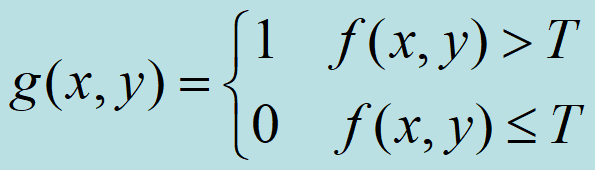《数字图像处理》第11讲——图像分割
虽然写这个博客主要目的是为了给我自己做一个思路记忆录,但是如果你恰好点了进来,那么先对你说一声欢迎。我并不是什么大触,只是一个菜菜的学生,如果您发现了什么错误或者您对于某些地方有更好的意见,非常欢迎您的斧正!
目录
独立点检测
线检测
边缘检测的梯度方法
梯度算子
Roberts交叉梯度算子
Priwitt梯度算子
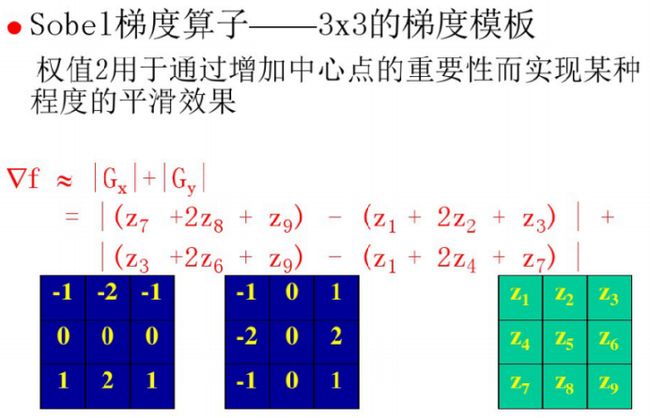
sobel梯度算子
拉普拉斯算子
高斯拉普拉斯算子
梯度模板求边缘总结
Hough变换
阀值
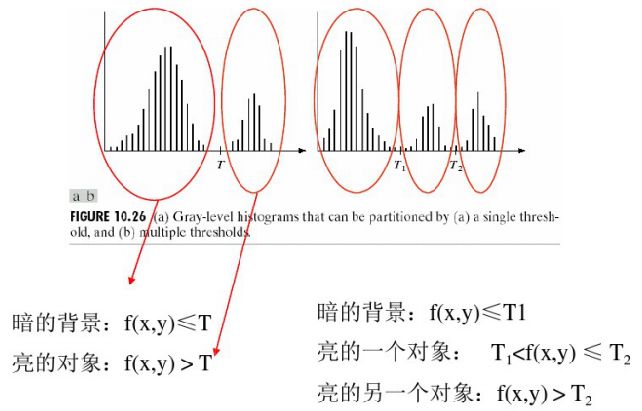
全局阀值
基本自适应域值
全局最佳门限和自适应门限
基于区域的分割
分水岭分割
参考文章及博客:
√图象分割就是指把图象分成各具特性的区域并提取出感兴趣目标的技术和过程。
·这里特性可以是灰度、颜色、纹理等,目标可以对应单个区域,也可以对应多个区域。
独立点检测
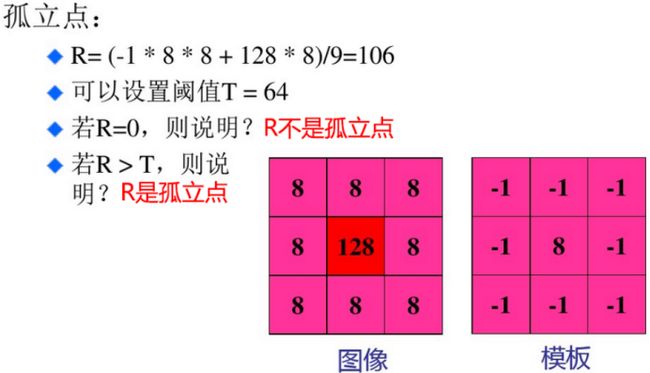
√基本思想:如果一个孤立点(此点的灰度级别和其背景的差别相当大,并且其所在的区域是一个均匀的或近似均匀的区域)与周围的点不同,则可以用指定模板检测。可以指定模板为为:
·根据检测图像的情况,设定R>T的输出响应对应孤立点。(T是阀值,R是模板计算值)
线检测
√线检测比点检测稍微复杂一点,其基本思想基本一致。
√表现在:
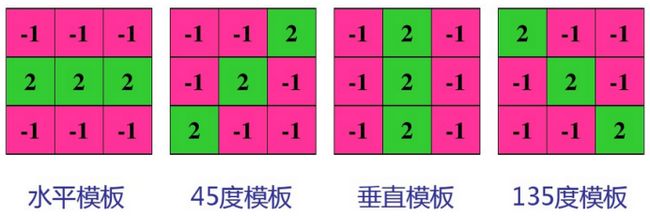
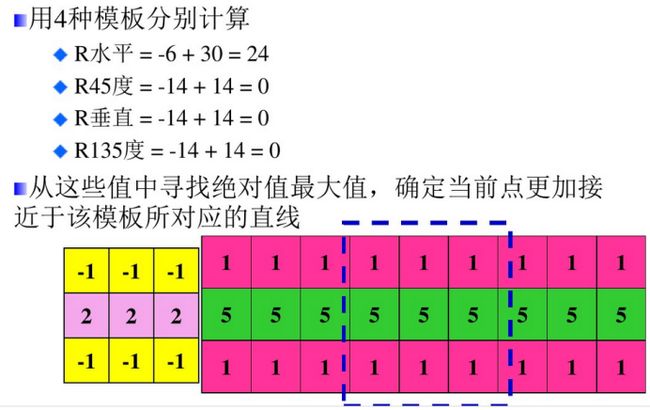
·使用模板(注意确定模板的条件或者基本假设)
·对输出响应决策,需要合适的决策方法。
√第一个模板对水平线有最大响应
√第二个模板对45°方向线有最大响应
√第三个模板对垂直线有最大响应
√第四个模板对-45°方向线有最大响应
边缘检测的梯度方法
√边缘是一个相对局部的概念,而边界是一个更具有整体性的一个概念。
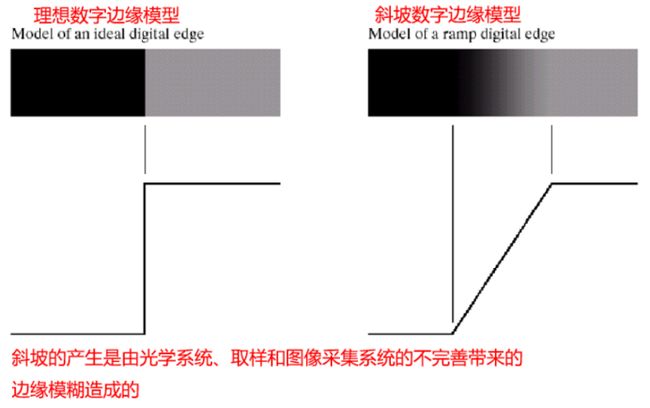
√边缘理想数字模型和模糊边缘
√模糊的边缘使两个区域过渡的范围变宽,因此边界较宽;反之,清晰的图像使其边缘变细。
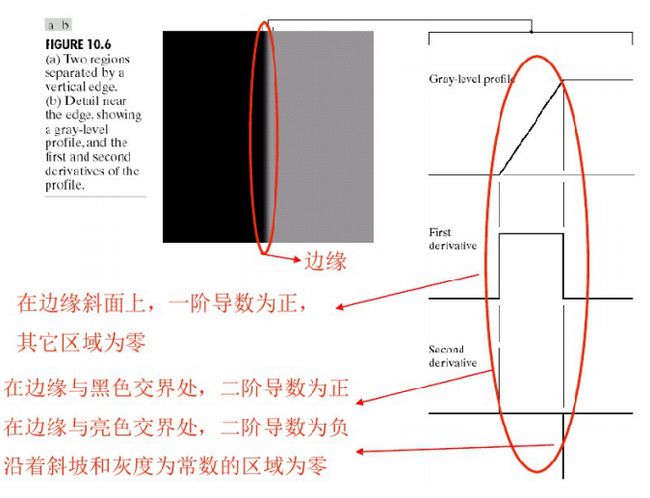
√一阶导数、二阶导数响应的特点
√结论
·一阶导数可用于检测图像中的一个点是否在边缘上
·二阶导数可以判断一个边缘像素是在边缘亮的一边还是暗的一边
·一条连接二阶导数正值和负值的虚构直线将在边缘中点附近穿过零点
·一阶导数使用梯度算子,二阶导数使用拉普拉斯算子
梯度算子
√连续图像f (x,y)在位置(x,y)的梯度定义为下列向量:
Roberts交叉梯度算子
Priwitt梯度算子
sobel梯度算子
Prewitt和Sobel算子是计算数字梯度时最常用的算子。
√Prewitt模板比Sobel模板简单,但Sobel模板能够有效抑制噪声。
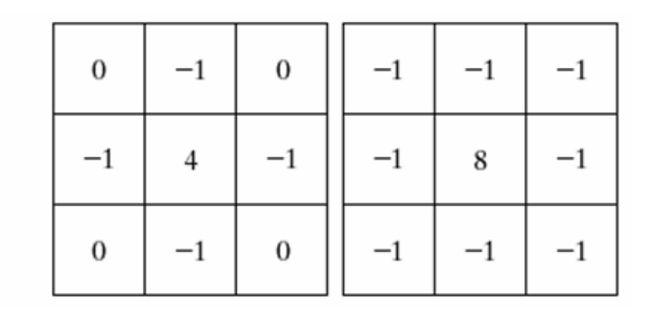
拉普拉斯算子
√二维函数f(x,y)的拉普拉斯算子是如下定义的:
√Laplacian 算子模板
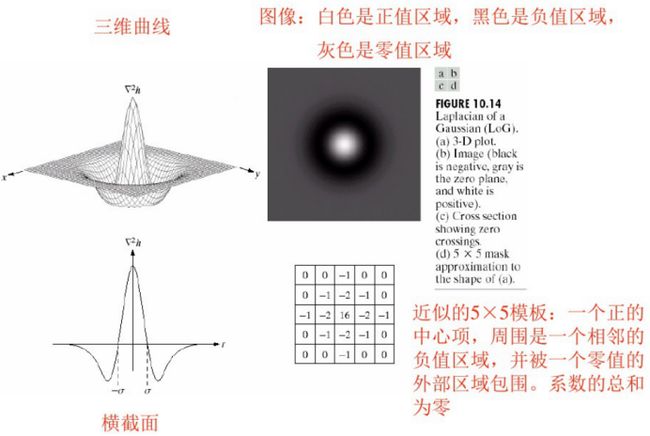
高斯拉普拉斯算子
√定义:
梯度模板求边缘总结
√拉普拉斯算子
缺点:
·对噪声具有敏感性
·幅值产生双边缘
·不能检测边缘的方向
优点
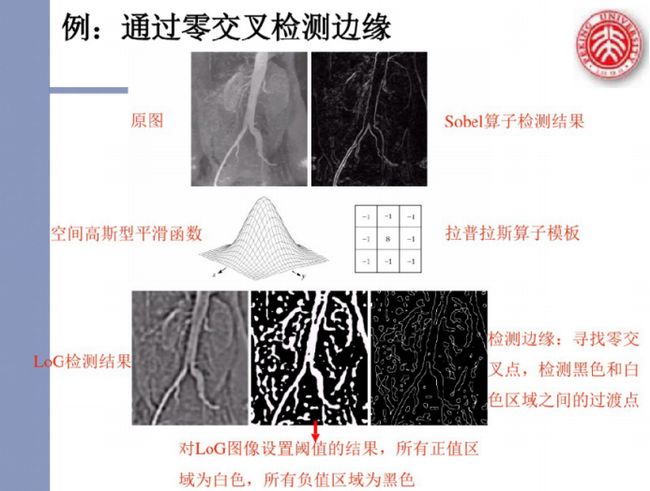
·可以利用零交叉的性质进行边缘定位
·可以确定一个像素是在边缘暗的一边还是亮的一边。
√高斯拉普拉斯算子
·目的是对图像进行平滑处理
·平滑处理减少了噪声的影响
Hough变换
√问题的提出:
√基本思想
阀值
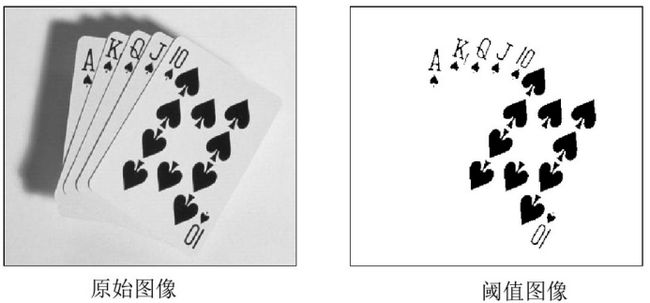
√阀值处理操作:
f(x,y)是点(x,y)的灰度级,p(x,y)表示该点的局部性质,如以(x,y)为中心的邻域的平均灰度级。
√对于门限T数学的形式表示:
全局阀值
基本自适应域值
√单一全局阀值存在的问题:不均匀亮度图像无法有效分割
√方法:将图像进一步细分为子图像,并对不同的子图像使用不同的阀值处理。
全局最佳门限和自适应门限
√假设一幅图像仅保安两个主要的灰度级区域。令z表示灰度级值,则两个灰度区域的直方图可以看做它们概率密度函数(PDF)的估计p(z)
√p(z)是两个密度的和或混合。一个是图像中亮区域的密度,另一个是暗区域的密度。
√如果p(z)已知或假设,则它能确定一个最佳阀值(具有最低的误差)将图像分割为两个可分的区域。
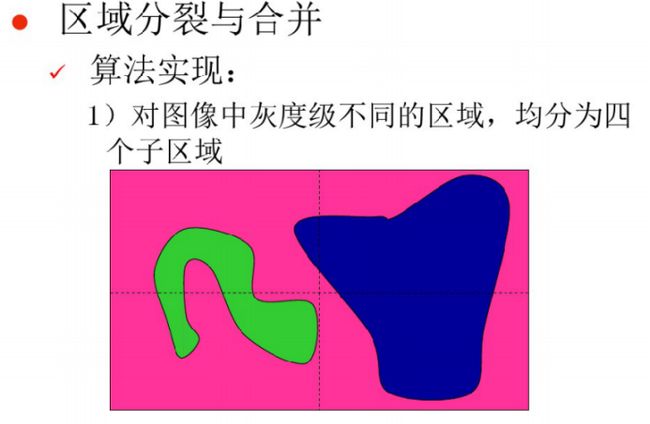
基于区域的分割
√生长算法
分水岭分割
√灰度图像的分水岭算法,就是就灰度值模拟为山的高度。从低到高,分别代表山岭从盆地到分水岭的高度。基于这些概念的分割算法的主要目的是找出分水线。
·基本思想是:假设在每一区域的最小值的位置上打一个小洞并让水均匀上升速率从洞中涌出,从低到高掩模真个地形。当处在不同汇水盆地的水要聚合在一起时,修建大坝将阻值聚合。当水继续上升,当水面淹没说有分水岭时,大坝对应的边界,就是分水岭算法的分割线。
gif图是盗来的,不过解释的挺好。
参考文章及博客:
图像处理——分水岭算法
https://blog.csdn.net/fengye2two/article/details/79116105
一份优秀的PPT:
https://wenku.baidu.com/view/b8a718e12af90242a995e573.html?rec_flag=default&sxts=1545207925345