图论--Matlab实现最短路径算法
使用Matlab的graphshortestpath 函数,快速求得最短路径,详情请参照Matlab帮助文档。
graphshortestpath solves the shortest path problem in graph.
[DIST,PATH,PRED] = graphshortestpath(G,S) determines the single source
shortest paths from node S to all other nodes in the graph G. Weights of
the edges are all nonzero entries in the n-by-n adjacency matrix
represented by the sparse matrix G. DIST are the n distances from source
to every node (using Inf for non-reachable nodes and zero for the source
node). The PATH contains the winning paths to every node, and PRED
contains the predecessor nodes of the winning paths.
[DIST,PATH,PRED] = graphshortestpath(G,S,D) determines the single
source-single destination shortest path from node S to node D.
graphshortestpath(...,'METHOD',METHOD) selects the algorithm to use,
options are:
'BFS' - Breadth First Search, assumes all the weights are
equal, edges are nonzero entries in the sparse matrix
G. Time complexity is O(n+e).
['Dijkstra'] - Assumes that weights of the edges are all positive
values in the sparse matrix G. Time complexity is
O(log(n)*e).
'Bellman-Ford' - Assumes that weights of the edges are all nonzero
entries in the sparse matrix G. Time complexity is
O(n*e).
'Acyclic' - The input graph must be acyclic. Assumes that weights
of the edges are all nonzero entries in the sparse
matrix G. Time complexity is O(n+e).
Note: n and e are number of nodes and edges respectively.
graphshortestpath(...,'DIRECTED',false) indicates that the graph G is
undirected, upper triangle of the sparse matrix is ignored. Default is
true.
graphshortestpath(...,'WEIGHTS',W) provides custom weights for the edges,
useful to indicate zero valued weights. W is a column vector with one
entry for every edge in G, traversed column-wise.
Examples:
% Create a directed graph with 6 nodes and 11 edges
W = [.41 .99 .51 .32 .15 .45 .38 .32 .36 .29 .21];
DG = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],W)
h = view(biograph(DG,[],'ShowWeights','on'))
% Find shortest path from 1 to 6
[dist,path,pred] = graphshortestpath(DG,1,6)
% Mark the nodes and edges of the shortest path
set(h.Nodes(path),'Color',[1 0.4 0.4])
edges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));
set(edges,'LineColor',[1 0 0])
set(edges,'LineWidth',1.5)
% Solving the previous problem for an undirected graph
UG = tril(DG + DG')
h = view(biograph(UG,[],'ShowArrows','off','ShowWeights','on'))
% Find the shortest path between node 1 and 6
[dist,path,pred] = graphshortestpath(UG,1,6,'directed',false)
% Mark the nodes and edges of the shortest path
set(h.Nodes(path),'Color',[1 0.4 0.4])
fowEdges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));
revEdges = getedgesbynodeid(h,get(h.Nodes(fliplr(path)),'ID'));
edges = [fowEdges;revEdges];
set(edges,'LineColor',[1 0 0])
set(edges,'LineWidth',1.5)
See also: graphallshortestpaths, graphconncomp, graphisdag,
graphisomorphism, graphisspantree, graphmaxflow, graphminspantree,
graphpred2path, graphtheorydemo, graphtopoorder, graphtraverse.
References:
[1] E.W. Dijkstra "A note on two problems in connexion with graphs"
Numerische Mathematik, 1:269-271, 1959.
[2] R. Bellman "On a Routing Problem" Quarterly of Applied Mathematics,
16(1):87-90, 1958.
Reference page in Help browser
doc graphshortestpath
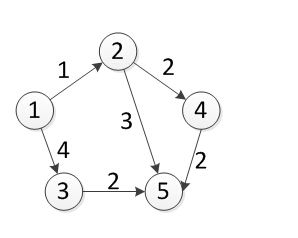
又帮助文档可知, 在Matlab中首先需要获取图的稀疏矩阵DG,为减小存储空间,我们通常以sparse函数得到。对于下图所示的有向带权图,先输入起始节点向量S = [1 1 2 2 3 4];(其中S(i)为第i条弧的始端节点号),然后输入终点节点向量E = [2 3 4 5 5 5];(其中E(i)为第i条弧的终点节点号),最后输入权向量W = [1 4 2 3 2 2];(其中W(i)为第i条弧的权值),利用DG = sparse(S,E,W);可得到稀疏矩阵。
接下来,只需要调用graphshortestpath 函数即可。(为方便最短路径的可视化,Matlab提供函数biograph来显示图的结构)。
代码如下:
s = [1 1 2 2 3 4]; % 起始节点向量 e = [2 3 4 5 5 5]; % 终止节点向量 w = [1 4 2 3 2 2]; % 权向量 g = sparse(s,e,w); % 构建稀疏矩阵 g(5,5)=0; % 使稀疏矩阵其余元素为0 p=biograph(g,[],'ShowWeights','on');%建立有向图对象P h=view(p);%显示各个路径权值 % 求节点1到节点5的最短路径 [Dist,Path]=graphshortestpath(g,1,5,'Method','Dijkstra') % 将最短路径的结点以红色显示 set(h.Nodes(Path),'Color',[1 0.4 0.4]); % 将最短路径的弧以红色显示 edges=getedgesbynodeid(h,get(h.Nodes(Path),'ID')); set(edges,'LineColor',[1 0 0]); set(edges,'LineWidth',2.0);
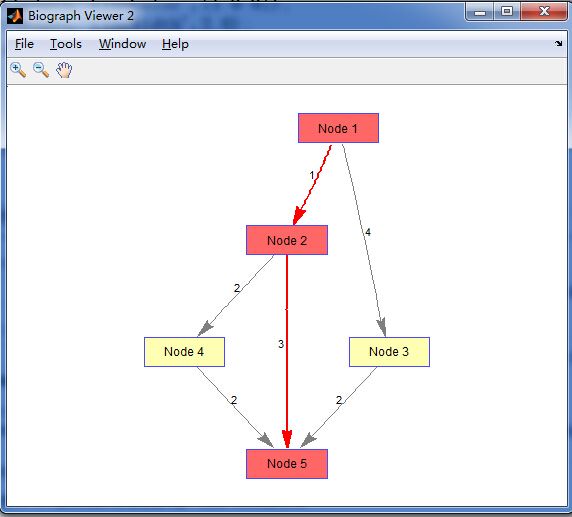
运行效果为:
另外,利用graphallshortestpaths函数,可以求出所有结点之间的最短路径,如下:
>> Dists=graphallshortestpaths(g) %求所有最短路径 Dists = 0 1 4 3 4 Inf 0 Inf 2 3 Inf Inf 0 Inf 2 Inf Inf Inf 0 2 Inf Inf Inf Inf 0