视觉SLAM理论与实践6-2
视觉SLAM理论与实践-直接法
- 一、直接法基础介绍
- 二、单层直接法
- 三、多层直接法
- 四、延申讨论
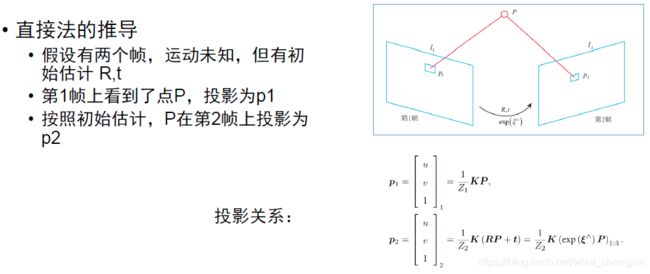
一、直接法基础介绍
二、单层直接法
- 该问题的误差项为:
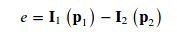
其中p1,p2 为非其次像素坐标,ξ为R,t对应的李代数


- 本题目中位姿的自由度为6,误差函数中的光度的变化是1维的数据,所以雅克比矩阵为1×6,误差项相对于自变量的雅克比维度为1×6.求解过程如下:
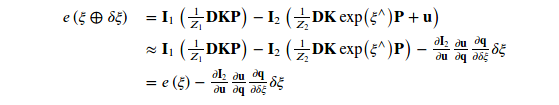
有上式可知,一阶导由于链式法则分成了3项,方便雅克比的计算,下面就是计算这三项。
第一项:
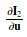
第二项:

第三项:

得到:

所以推到出来误差相对于李代数的雅克比矩阵为:
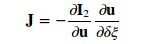
- 窗口大小的选择和误差以及计算量有关系。窗口不能取太大,随着窗口的增大,两帧之间的关键点的计算量将会呈指数增长;窗口可以取单点。但是这样会导致像素梯度计算误差增大。
三、多层直接法
#include <opencv2/opencv.hpp>
#include <sophus/se3.h>
#include <Eigen/Core>
#include <vector>
#include <string>
#include <boost/format.hpp>
#include <pangolin/pangolin.h>
using namespace std;
typedef vector<Eigen::Vector2d, Eigen::aligned_allocator<Eigen::Vector2d>>
VecVector2d;
// Camera intrinsics
// 内参
double fx = 718.856, fy = 718.856, cx = 607.1928, cy = 185.2157;
// 基线
double baseline = 0.573;
// paths
string left_file = "../left.png";
string disparity_file = "../disparity.png";
boost::format fmt_others("../%06d.png"); // other files
// useful typedefs
typedef Eigen::Matrix<double, 6, 6> Matrix6d;
typedef Eigen::Matrix<double, 2, 6> Matrix26d;
typedef Eigen::Matrix<double, 6, 1> Vector6d;
// TODO implement this function
/**
* pose estimation using direct method
* @param img1
* @param img2
* @param px_ref
* @param depth_ref
* @param T21
*/
void DirectPoseEstimationMultiLayer(
const cv::Mat &img1,
const cv::Mat &img2,
const VecVector2d &px_ref,
const vector<double> depth_ref,
Sophus::SE3 &T21
);
// TODO implement this function
/**
* pose estimation using direct method
* @param img1
* @param img2
* @param px_ref
* @param depth_ref
* @param T21
*/
void DirectPoseEstimationSingleLayer(
const cv::Mat &img1,
const cv::Mat &img2,
const VecVector2d &px_ref,
const vector<double> depth_ref,
Sophus::SE3 &T21
);
// bilinear interpolation
inline float GetPixelValue(const cv::Mat &img, float x, float y) {
uchar *data = &img.data[int(y) * img.step + int(x)];
float xx = x - floor(x);
float yy = y - floor(y);
return float(
(1 - xx) * (1 - yy) * data[0] +
xx * (1 - yy) * data[1] +
(1 - xx) * yy * data[img.step] +
xx * yy * data[img.step + 1]
);
}
int main(int argc, char **argv) {
cv::Mat left_img = cv::imread(left_file, 0);
cv::Mat disparity_img = cv::imread(disparity_file, 0);
// let's randomly pick pixels in the first image and generate some 3d
points in the first image's frame
cv::RNG rng;
int nPoints = 1000;
int boarder = 40;
VecVector2d pixels_ref;
vector<double> depth_ref;
// generate pixels in ref and load depth data
for (int i = 0; i < nPoints; i++) {
int x = rng.uniform(boarder, left_img.cols - boarder); // don't pick
pixels close to boarder
int y = rng.uniform(boarder, left_img.rows - boarder); // don't pick
pixels close to boarder
int disparity = disparity_img.at<uchar>(y, x);
double depth = fx * baseline / disparity; // you know this is disparity
to depth
depth_ref.push_back(depth);
pixels_ref.push_back(Eigen::Vector2d(x, y));
}
// estimates 01~05.png's pose using this information
Sophus::SE3 T_cur_ref;
for (int i = 1; i < 6; i++) { // 1~10
cv::Mat img = cv::imread((fmt_others % i).str(), 0);
// DirectPoseEstimationSingleLayer(left_img, img, pixels_ref,
depth_ref, T_cur_ref); // first you need to test single layer
DirectPoseEstimationMultiLayer(left_img, img, pixels_ref, depth_ref,
T_cur_ref);
}
}
void DirectPoseEstimationSingleLayer(
const cv::Mat &img1,
const cv::Mat &img2,
const VecVector2d &px_ref,
const vector<double> depth_ref,
Sophus::SE3 &T21
) {
// parameters
int half_patch_size = 4;
int iterations = 100;
double cost = 0, lastCost = 0;
int nGood = 0; // good projections
VecVector2d goodProjection;
for (int iter = 0; iter < iterations; iter++) {
nGood = 0;
goodProjection.clear();
// Define Hessian and bias
Matrix6d H = Matrix6d::Zero(); // 6x6 Hessian
Vector6d b = Vector6d::Zero(); // 6x1 bias
for (size_t i = 0; i < px_ref.size(); i++) {
// compute the projection in the second image
// TODO START YOUR CODE HERE
float u =px_ref[i][0], v = px_ref[i][1];
double depth = depth_ref[i];
double xc2_opt = 0,yc2_opt = 0,zc2_opt = 0;
float u2_opt = 0, v2_opt = 0;
double xc1 = double((u - cx)*depth/fx);
double yc1 = double((v-cy)*depth/fy);
Eigen::Vector3d pc1(xc1,yc1,depth);
Eigen::Vector3d pc2 = T21*pc1;
xc2_opt = pc2[0]; yc2_opt = pc2[1];zc2_opt = pc2[2];
u2_opt = float(fx*xc2_opt/zc2_opt+cx);
v2_opt = float(fy*yc2_opt/zc2_opt+cy);
if(u-4<0 || u+4>=img1.cols || v-4 <0 || v+4>=img1.rows ||
u2_opt-4<0 || u2_opt+4>=img2.cols || v2_opt -4<0 ||
v2_opt>=img2.rows)
{
continue;
}
nGood++;
goodProjection.push_back(Eigen::Vector2d(u2_opt, v2_opt));
// and compute error and jacobian
for (int x = -half_patch_size; x < half_patch_size; x++)
for (int y = -half_patch_size; y < half_patch_size; y++) {
float u1 = float(u+x), v1 = float(v+y);
float u2 = float(u2_opt+x), v2 = float(v2_opt+y);
double error =GetPixelValue(img1,u1,v1) - GetPixelValue(img2,
u2,v2);
//double error =0;
Matrix26d J_pixel_xi= Matrix26d::Zero(); // pixel to \xi in
Lie algebra
Eigen::Vector2d J_img_pixel= Eigen::Vector2d::Zero(); //
image gradients
if(u2-1<0 || u2+1>=img2.cols || v2-1<0 || v2+1>img2.rows)
{
continue;
}
J_img_pixel[0] = (GetPixelValue(img2,u2+1,v2) -
GetPixelValue(img2,u2-1,v2))/2;
J_img_pixel[1] = (GetPixelValue(img2,u2,v2+1) -
GetPixelValue(img2,u2,v2-1))/2;
// total jacobian
J_pixel_xi(0,0) = fx/zc2_opt;
J_pixel_xi(0,2) = -fx * xc2_opt/(zc2_opt*zc2_opt);
J_pixel_xi(0,3) = - fx * xc2_opt * yc2_opt / (zc2_opt*zc2_opt);
J_pixel_xi(0,4) = fx + fx * xc2_opt*zc2_opt /(zc2_opt*zc2_opt);
J_pixel_xi(0,5) = - fx * yc2_opt / zc2_opt;
J_pixel_xi(1,1) = fy / zc2_opt;
J_pixel_xi(1,2) = -fy * yc2_opt / (zc2_opt*zc2_opt);
J_pixel_xi(1,3) = -fy - fy * yc2_opt*yc2_opt /
(zc2_opt*zc2_opt);
J_pixel_xi(1,4) = fy * xc2_opt * yc2_opt / (zc2_opt*zc2_opt);
J_pixel_xi(1,5) = fy * xc2_opt / zc2_opt;
Vector6d J = -J_pixel_xi.transpose()*J_img_pixel;
H += J * J.transpose();
b += -error * J;
cost += error * error;
}
// END YOUR CODE HERE
}
// solve update and put it into estimation
// TODO START YOUR CODE HERE
Vector6d update;
update = H.ldlt().solve(b);
T21 = Sophus::SE3::exp(update) * T21;
// END YOUR CODE HERE
cost /= nGood;
if (isnan(update[0])) {
// sometimes occurred when we have a black or white patch and H is
irreversible
cout << "update is nan" << endl;
break;
}
if (iter > 0 && cost > lastCost) {
cout << "cost increased: " << cost << ", " << lastCost << endl;
break;
}
lastCost = cost;
cout << "cost = " << cost << ", good = " << nGood << endl;
}
cout << "good projection: " << nGood << endl;
cout << "T21 = \n" << T21.matrix() << endl;
// in order to help you debug, we plot the projected pixels here
cv::Mat img1_show, img2_show;
cv::cvtColor(img1, img1_show, CV_GRAY2BGR);
cv::cvtColor(img2, img2_show, CV_GRAY2BGR);
for (auto &px: px_ref) {
cv::rectangle(img1_show, cv::Point2f(px[0] - 2, px[1] - 2),
cv::Point2f(px[0] + 2, px[1] + 2),
cv::Scalar(0, 250, 0));
}
for (auto &px: goodProjection) {
cv::rectangle(img2_show, cv::Point2f(px[0] - 2, px[1] - 2),
cv::Point2f(px[0] + 2, px[1] + 2),
cv::Scalar(0, 250, 0));
}
cv::imshow("reference", img1_show);
cv::imshow("current", img2_show);
cv::waitKey();
}
void DirectPoseEstimationMultiLayer(
const cv::Mat &img1,
const cv::Mat &img2,
const VecVector2d &px_ref,
const vector<double> depth_ref,
Sophus::SE3 &T21
) {
// parameters
int pyramids = 4;
double pyramid_scale = 0.5;
double scales[] = {1.0, 0.5, 0.25, 0.125};
// create pyramids
vector<cv::Mat> pyr1, pyr2; // image pyramids
// TODO START YOUR CODE HERE
for(int i = 0;i<pyramids;i++)
{
cv::Mat img1_temp, img2_temp;
cv::resize(img1, img1_temp,
cv::Size(img1.cols*scales[i],img2.rows*scales[i]) );
cv::resize(img2,img2_temp, cv::Size(img2.cols*scales[i],
img2.rows*scales[i]));
pyr1.push_back(img1_temp);
pyr2.push_back(img2_temp);
}
// END YOUR CODE HERE
double fxG = fx, fyG = fy, cxG = cx, cyG = cy; // backup the old values
for (int level = pyramids - 1; level >= 0; level--) {
VecVector2d px_ref_pyr; // set the keypoints in this pyramid level
for (auto &px: px_ref) {
px_ref_pyr.push_back(scales[level] * px);
}
// TODO START YOUR CODE HERE
// scale fx, fy, cx, cy in different pyramid levels
fx = fxG*scales[level];
fy = fyG*scales[level];
cx = cxG*scales[level];
cy = cyG*scales[level];
// END YOUR CODE HERE
DirectPoseEstimationSingleLayer(pyr1[level], pyr2[level], px_ref_pyr,
depth_ref, T21);
}
}
四、延申讨论
-
从本次作业的理解来看,直接法实现原理与光流类似,应该可以类似与光流提出inverse,compositional的概念
-
加速思路是否可以更改窗口大小,怎么改???
-
灰度值不变和深度值不变
-
只要是该点存在梯度值,就可以被提取到。
一条线上的点可能某个方向上存在相同的梯度值,有时无法准确估计该路标点的位置。所以一般不用线上的点。碰到白墙跟踪结果可能有偏差。 -
直接法优点:
实时性更好一些,因为省略了计算描述子的时间
缺点:
灰度不变的假设性太强了,物体有高光或者阴影,相机运动过快时均容易失败。
特征点法优点:
对光照有一定的容忍度,系统鲁棒性较高。
特征点法缺点:
前端占用计算资源过大,实时性相比较而言较低。碰到纹理较少的地方,跟踪容易失败。
友情提示:代码下载需要C币,请事先判断是否对您有帮助,谨慎下载哦!!!