Chernoff bound(chernoff-hoeffding bound)
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables. It is a sharper bound than the known first or second moment based tail bounds such as Markov's inequality or Chebyshev inequality, which only yield power-law bounds on tail decay. However, the Chernoff bound requires that the variates be independent - a condition that neither the Markov nor the Chebyshev inequalities require.
It is related to the (historically earliest) Bernstein inequalities, and to Hoeffding's inequality.
Definition
Let X1, ..., Xn be independent Bernoulli random variables, each having probability p > 1/2. Then the probability of simultaneous occurrence of more than n/2 of the events ![]() has an exact value S, where
has an exact value S, where
The Chernoff bound shows that S has the following lower bound:
-
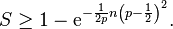
- 之上的S表示概率.
- 之下的S表示事件发生的总次数.
- 上面的式子就是
Indeed, noticing that ![]() , we get by the multiplicative form of Chernoff bound (see below or Corollary 13.3 in Sinclair's class notes),
, we get by the multiplicative form of Chernoff bound (see below or Corollary 13.3 in Sinclair's class notes),
This result admits various generalizations as outlined below. One can encounter many flavours of Chernoff bounds: the original additive form (which gives a bound on the absolute error) or the more practical multiplicative form (which bounds the error relative to the mean).
[edit]A motivating example
The simplest case of Chernoff bounds is used to bound the success probability of majority agreement for n independent, equally likely events.
A simple motivating example is to consider a biased coin. One side (say, Heads), is more likely to come up than the other, but you don't know which and would like to find out. The obvious solution is to flip it many times and then choose the side that comes up the most. But how many times do you have to flip it to be confident that you've chosen correctly?
In our example, let ![]() denote the event that the ith coin flip comes up Heads; suppose that we want to ensure we choose the wrong side with at most a small probability ε. Then, rearranging the above, we must have:
denote the event that the ith coin flip comes up Heads; suppose that we want to ensure we choose the wrong side with at most a small probability ε. Then, rearranging the above, we must have:
If the coin is noticeably biased, say coming up on one side 60% of the time (p = .6), then we can guess that side with 95% (![]() ) accuracy after 150 flips
) accuracy after 150 flips![]() . If it is 90% biased, then a mere 10 flips suffices. If the coin is only biased a tiny amount, like most real coins are, the number of necessary flips becomes much larger.
. If it is 90% biased, then a mere 10 flips suffices. If the coin is only biased a tiny amount, like most real coins are, the number of necessary flips becomes much larger.
More practically, the Chernoff bound is used in randomized algorithms (or in computational devices such as quantum computers) to determine a bound on the number of runs necessary to determine a value by majority agreement, up to a specified probability. For example, suppose an algorithm (or machine) A computes the correct value of a function f with probability p > 1/2. If we choose nsatisfying the inequality above, the probability that a majority exists and is equal to the correct value is at least 1 − ε, which for small enough ε is quite reliable. If p is a constant, ε diminishes exponentially with growing n, which is what makes algorithms in the complexity class BPP efficient.
Notice that if p is very close to 1/2, the necessary n can become very large. For example, if p = 1/2 + 1/2m, as it might be in some PPalgorithms, the result is that n is bounded below by an exponential function in m:
The first step in the proof of Chernoff bounds
The Chernoff bound for a random variable X, which is the sum of n independent random variables ![]() , is obtained by applying etX for some well-chosen value of t. This method was first applied by Sergei Bernstein to prove the related Bernstein inequalities.
, is obtained by applying etX for some well-chosen value of t. This method was first applied by Sergei Bernstein to prove the related Bernstein inequalities.
From Markov's inequality and using independence we can derive the following useful inequality:
For any t > 0,
In particular optimizing over t and using independence we obtain,
Similarly,
and so,
[edit]Precise statements and proofs
[edit]Theorem for additive form (absolute error)
The following Theorem is due to Wassily Hoeffding and hence is called Chernoff-Hoeffding theorem.
Assume random variables ![]() are i.i.d. Let
are i.i.d. Let ![]() ,
, ![]() , and
, and ![]() . Then
. Then
and
where
is the Kullback-Leibler divergence between Bernoulli distributed random variables with parameters ![]() and
and ![]() respectively. If
respectively. If ![]() , then
, then ![]()
[edit]Proof
The proof starts from the general inequality (1) above. ![]() . Taking a = mq in (1), we obtain:
. Taking a = mq in (1), we obtain:
Now, knowing that ![]() ,
, ![]() , we have
, we have
Therefore we can easily compute the infimum, using calculus and some logarithms. Thus,
Setting the last equation to zero and solving, we have
As ![]() , we see that
, we see that ![]() , so our bound is satisfied on
, so our bound is satisfied on ![]() . Having solved for
. Having solved for ![]() , we can plug back into the equations above to find that
, we can plug back into the equations above to find that
We now have our desired result, that
To complete the proof for the symmetric case, we simply define the random variable ![]() , apply the same proof, and plug it into our bound.
, apply the same proof, and plug it into our bound.
[edit]Simpler bounds
A simpler bound follows by relaxing the theorem using ![]() , which follows from the convexity of
, which follows from the convexity of ![]() and the fact that
and the fact that ![]() . This results in a special case of Hoeffding's inequality. Sometimes, the bound
. This results in a special case of Hoeffding's inequality. Sometimes, the bound ![]() for
for ![]() , which is stronger for
, which is stronger for ![]() , is also used.
, is also used.
[edit]Theorem for multiplicative form of Chernoff bound (relative error)
Let random variables ![]() be independent random variables taking on values 0 or 1. Further, assume that
be independent random variables taking on values 0 or 1. Further, assume that ![]() . Then, if we let
. Then, if we let ![]() and
and ![]() be the expectation of
be the expectation of ![]() , for any
, for any ![]()
[edit]Proof
According to (1),
The third line above follows because ![]() takes the value
takes the value ![]() with probability
with probability ![]() and the value
and the value ![]() with probability
with probability ![]() . This is identical to the calculation above in the proof of the Theorem for additive form (absolute error).
. This is identical to the calculation above in the proof of the Theorem for additive form (absolute error).
Rewriting ![]() as
as ![]() and recalling that
and recalling that ![]() (with strict inequality if
(with strict inequality if ![]() ), we set
), we set ![]() . The same result can be obtained by directly replacinga in the equation for the Chernoff bound with
. The same result can be obtained by directly replacinga in the equation for the Chernoff bound with ![]() .[1]
.[1]
Thus,
If we simply set ![]() so that
so that ![]() for
for ![]() , we can substitute and find
, we can substitute and find
This proves the result desired. A similar proof strategy can be used to show that
[edit]Better Chernoff bounds for some special cases
We can obtain stronger bounds using simpler proof techniques for some special cases of symmetric random variables.
Let ![]() be independent random variables,
be independent random variables,
Then,
-
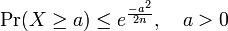 ,
,
and therefore also
-
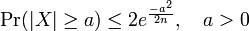 .
.
Then,
-
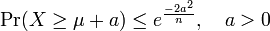 ,
,
-
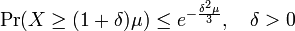 ,
,
-
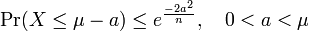 ,
,
-
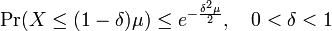 .
.
[edit]Applications of Chernoff bound
Chernoff bounds have very useful applications in set balancing and packet routing in sparse networks.
The set balancing problem arises while designing statistical experiments. Typically while designing a statistical experiment, given the features of each participant in the experiment, we need to know how to divide the participants into 2 disjoint groups such that each feature is roughly as balanced as possible between the two groups. Refer to this book section for more info on the problem.
Chernoff bounds are also used to obtain tight bounds for permutation routing problems which reduce network congestion while routing packets in sparse networks. Refer to this book section for a thorough treatment of the problem.
[edit]Matrix Chernoff bound
Rudolf Ahlswede and Andreas Winter introduced (Ahlswede & Winter 2003) a Chernoff bound for matrix-valued random variables.
If ![]() is distributed according to some distribution over
is distributed according to some distribution over ![]() matrices with zero mean, and if
matrices with zero mean, and if ![]() are independent copies of
are independent copies of ![]() then for any
then for any ![]() ,
,
where ![]() holds almost surely and
holds almost surely and ![]() is an absolute constant.
is an absolute constant.
Notice that the number of samples in the inequality depends logarithmically on ![]() . In general, unfortunately, such a dependency is inevitable: take for example a diagonal random sign matrix of dimension
. In general, unfortunately, such a dependency is inevitable: take for example a diagonal random sign matrix of dimension ![]() . The operator norm of the sum of
. The operator norm of the sum of ![]() independent samples is precisely the maximum deviation among
independent samples is precisely the maximum deviation among ![]() independent random walks of length
independent random walks of length ![]() . In order to achieve a fixed bound on the maximum deviation with constant probability, it is easy to see that
. In order to achieve a fixed bound on the maximum deviation with constant probability, it is easy to see that ![]() should grow logarithmically with
should grow logarithmically with ![]() in this scenario.[2]
in this scenario.[2]
The following theorem can be obtained by assuming ![]() has low rank, in order to avoid the dependency on the dimensions.
has low rank, in order to avoid the dependency on the dimensions.
[edit]Theorem without the dependency on the dimensions
Let ![]() and
and ![]() be a random symmetric real matrix with
be a random symmetric real matrix with ![]() and
and ![]() almost surely. Assume that each element on the support of
almost surely. Assume that each element on the support of ![]() has at most rank
has at most rank ![]() . Set
. Set
If ![]() holds almost surely, then
holds almost surely, then
where ![]() are i.i.d. copies of
are i.i.d. copies of ![]() .
.
From: http://en.wikipedia.org/wiki/Chernoff_bound




![Chernoff <wbr>bound P\left[S\le\frac{n}{2}\right]=P\left[S\le\left(1-\left(1-\frac{1}{2p}\right)\right)\mu\right]\leq e^{-\frac{\mu}{2}\left(1-\frac{1}{2p}\right)^2}=e^{-\frac{1}{2p}n\left(p-\frac{1}{2}\right)^2}](http://img.e-com-net.com/image/info8/3767725f13ad45f8b449275019b102fd.png)
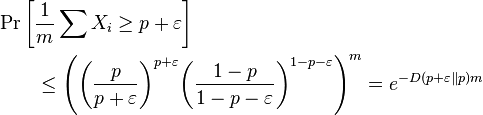
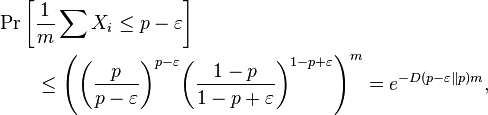
![Chernoff <wbr>bound \Pr\left[ \frac{1}{m} \sum X_i \ge q\right] \le \inf_{t>0} \frac{E \left[\prod e^{t X_i}\right]}{e^{tmq}} = \inf_{t>0} \left[\frac{ E\left[e^{tX_i} \right] }{e^{tq}}\right]^m .](http://img.e-com-net.com/image/info8/79bddd0cfae84ab488503f20045dfa58.png)
![Chernoff <wbr>bound \left[\frac{ E\left[e^{tX_i} \right] }{e^{tq}}\right]^m = \left[\frac{p e^t + (1-p)}{e^{tq} }\right]^m = [pe^{(1-q)t} + (1-p)e^{-qt}]^m.](http://img.e-com-net.com/image/info8/44d037e13a20499e824d9ec9a218594b.png)
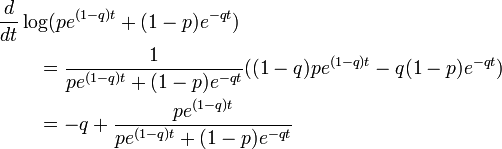




![Chernoff <wbr>bound \Pr \left[ X > (1+\delta)\mu\right] < \left(\frac{e^\delta}{(1+\delta)^{(1+\delta)}}\right)^\mu.](http://img.e-com-net.com/image/info8/702d04e82d574cf6ada25d4a7b66854f.png)

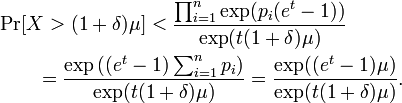
![Chernoff <wbr>bound \frac{\exp((e^t-1)\mu)}{\exp(t(1+\delta)\mu)} = \frac{\exp((1+\delta - 1)\mu)}{(1+\delta)^{(1+\delta)\mu}} = \left[\frac{\exp(\delta)}{(1+\delta)^{(1+\delta)}}\right]^\mu](http://img.e-com-net.com/image/info8/26fb86507ce14dd493bbc24a7fc55796.png)
![Chernoff <wbr>bound \Pr \left( \bigg\Vert \frac{1}{t} \sum_{i=1}^t M_i - \mathbf{E}[M] \bigg\Vert_2 > \varepsilon \right) \leq d \exp \left( -C \frac{\varepsilon^2 t}{\gamma^2} \right).](http://img.e-com-net.com/image/info8/b649fcbf4f7d41588c4303cbcca5a465.png)

![Chernoff <wbr>bound \Pr \left( \bigg\Vert \frac{1}{t} \sum_{i=1}^t M_i - \mathbf{E}[M] \bigg\Vert_2 > \varepsilon \right) \leq \frac{1}{\mathbf{poly}(t)}](http://img.e-com-net.com/image/info8/55b58231fadb49e89ad32ad4e41c1430.png)