去雾算法学习-----Automatic recovery of the atmospheric light hazy image(fattal 大气光值自适应去雾算法)阅读笔记
IEEE 2014
以色列 希伯来大学
Matan Sulami Itamar Glatzer Raanan Fattal Mike Werman
作者主页:http://www.cs.huji.ac.il/~raananf/
(1-t(x))A表现为环境光,A~表示矢量方向=A/||A||。
不精准的A会让t也不准确,由于t是用A求得的。不正确的A的模会导致术后出图像在亮度上的错误表现。并且这个多通道的偏差取决于t。当A偏大时,t小的地方(近景)会过曝,t大的地方(远景)会偏暗。而当A偏小时则相反。亮度的偏差依赖于t和图像的内容。
TAN认为最亮的像素充满了雾,是一个有雾区域的像素。
TAREL是基于灰度世界的假设,先对图像做白平衡,然后用A(1,1,1)进行去雾。
在这个算法中,将去雾分成了两个部分 1)求取A矢量的方向 2)求取A矢量的模长
求取方向A~
在去雾公式中,其中的J又可以表示成这样![]() ,其中l表示图像的明暗系数,反映亮度是一个标量;R表示图像表面反射系数,是一个矢量,反映了光的色度,并且||R||=1。
,其中l表示图像的明暗系数,反映亮度是一个标量;R表示图像表面反射系数,是一个矢量,反映了光的色度,并且||R||=1。
那么去雾公式可以写成![]() ,其中l(x)表示ti*l’(x),ti表示第i块内的透射率,Ri是第i块内的反射率。
,其中l(x)表示ti*l’(x),ti表示第i块内的透射率,Ri是第i块内的反射率。
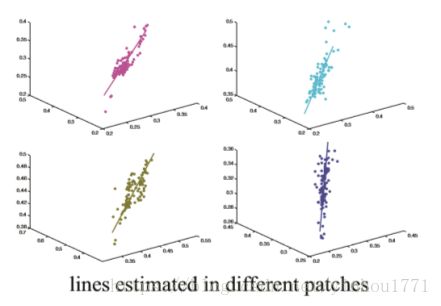
由于块具有局部平滑的特性。假设块内R和t保持不变。公式(3)可以理解为一个线性方程。那么一个块内的像素RGB会分布在一条直线上。且根据公式可知,这条线的方向为R矢量方向,偏移矢量为A~。
因此,每一个块的直线与原点形成一个平面,两个平面的交线就是候选向量。可以使用最少两个块或更多块的交点去恢复A~。
计算第i个块对应的直线和其对应的第j个候选向量计算最小欧式距离dij。对所有的dij进行排序,选取中值对应的那个块i。再从块i中选取其对应的距离dij最小的那个j个候选向量。这就是要求得的A~。用公式表示为![]() 。
。
上图可以看出,块内像素分布并不是完全的分布在直线上。块内下像素直线由所有像素的重心和PCA(主成分分析)过后的最大特征值对应的特征向量。
为了防止异常值,首先对块内所有像素进行一次PCA,计算出直线。然后剔除与直线距离最远的前20%个像素,再进行第二次PCA。
关于如何寻找符合公式(3)的块的步骤如下,假设![]() 是三个特征值:
是三个特征值:
- 第一特征向量是R矢量的方向,所以个坐标非负。
- 第一特征值大于阈值,
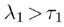 。
。 - 为了使像素能明显的处于一条直线附近,所以要有一个明确的第一特征值。
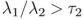 。
。 - 直线不能穿过原点,且与原点的欧式距离
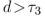 。
。 - 由于假设块内平滑,所以所选的块不能有边缘信息,在这里使用canny提取边缘信息,包含边缘像素的块将被丢弃。
在这一过程中,使用10*10的块。
关于![]()
![]() 的设定:首先分别单独初始化,使步骤2、3、4单独的每一个步骤能够找到大于50个块。然后计算同时满足2、3、4步骤的块,若小于10个,则对这三个参数轮流减少3%。直到满足。
的设定:首先分别单独初始化,使步骤2、3、4单独的每一个步骤能够找到大于50个块。然后计算同时满足2、3、4步骤的块,若小于10个,则对这三个参数轮流减少3%。直到满足。
另外,去除角度小于15°的直线对应的块。
求取模||A||
引入修正因子a。使得式子![]() 成立。
成立。
上式并不是只有唯一解,但是有一个特解可以成功去雾,(1-ta(x))aA应该与(1-t(x))A相匹配,因为其反映了环境光。
为了满足(4),R和A必须跨越正确的二维子空间,因此任何偏离的大气光值必须通过t和l来校正,并且t和l是相关的。
那么(5)中的式子被分解,意味着![]()
![]()
因为只有R定义了线性空间关系(矢量方向),且||R||=||Ra||=1。Ra=R。
所以使用aA作为大气光值去雾的结果为![]()
![]() ,与
,与![]()
![]() 的不同之处在于亮度上。
的不同之处在于亮度上。
当一个被低估了的aA(即a<1)会导致低t的地方更亮。相反高估了的aA(即a>1)会导致低t的地方更暗。
这些局部的偏差是难以被发现的,因为它与t是相关的,而t与图片内容相关。不同物体像素通常对应于相同的表面颜色和深度范围,因此在t和对象间的边界对应于J中的边缘,另外t的不连续是因为深度的变化。
为了解决这个问题,基于观察自然有雾图像的统计发现一个不变性,其证明如下。
将t的值划分成不同等级。
![]() 该公式表示当t(x)=s的所有像素中,输出亮度为第1%个像素的l值。
该公式表示当t(x)=s的所有像素中,输出亮度为第1%个像素的l值。
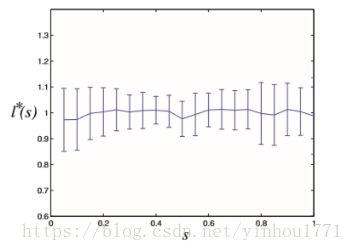
对于多幅图像统计计算l*的均值和方差,其结果如下。
发现对应于不同的t和图像,具有不变性。不同图片的各个等级的t的第1%个像素的l值基本保持一致。其原因是大体积的物体在图像中占据了一个小范围的t(或者景深)。
在实际操作中使用aA作为大气光值去雾后的图像Ja(x)进行统计![]()
根据式子(5)(6)可以推出![]() 。把这个从l*(s)到la*的转换归因于错误的估计了大气光值的大小。
。把这个从l*(s)到la*的转换归因于错误的估计了大气光值的大小。
由于上面提到的不变性,可以将l*看作一个常数k。最后通过如下式子求得最终的修正因子a。
![]() ,并且用matlab中的fminsearch解,初始化a~=1,k=1;
,并且用matlab中的fminsearch解,初始化a~=1,k=1;
算法步骤:
- 筛选符合要求的块
- 两两块平面相交求取候选向量
- 从所有候选向量中选取中值对应的块i。选择块i的所有dij距离中的最小值对应候选向量为A~
- 根据A~将其归一化,使得||A||=1,使用这个作为大气光值去雾
- 使用方程
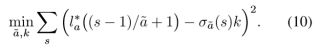 计算a~
计算a~ - A~/a~作为正确的大气光值进行最后的去雾。
局限
- 部分图像不符合l*的不变性,会估计出错误的模
- 部分图像找不到满足要求的足够多的块参与候选向量选择
以下效果仅用了算法中的方向的算法,并未使用模长估计,而是使用了自己的算法。
原论文完整matlab代码在作者的主页有,可以供下载。
个人不好实验结果:
A=0.72 0.74 0.42
A=0.96 0.86 0.79
个人实验正确的结果:
A=0.82 0.88 0.92
A=0.75 0.77 0.80
在这里只看整体颜色趋势,而忽略A的大小。
在我的整体测试图片中,部分的图片效果并不好。
原有有二:1、部分图像估计出来的A的方向就不对。
2、模估计大小存在问题,导致图像增强的幅度过大,最终导致偏色。