【Matlab】【机器学习】SVM快速算法 - SMO(序列最小优化)从推理到实现
支持向量机(SVM)---------------------------------------------------------
支持向量机(support vector machines, SVM)是一种监督二分类模型,具有完善的数学理论,其目标函数具有良好的凸性,可直接运用凸优化方法一次性找到最佳分类超平面。
设
K i j = K ( x i , x j ) K_{ij}=K(x_i,x_j) Kij=K(xi,xj)
是数据向量 x i x_i xi和 x j x_j xj的内积,可以是线性内积(线性核函数),也可以是高斯内积(高斯核函数)。若为高斯内积,则为非线性SVM。
由内积表达式,有
K i j = K j i K_{ij}=K_{ji} Kij=Kji
则SVM的优化目标可写为:
max α i J = ∑ i = 1 N α i − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) s . t . { 0 ≤ α i ≤ C ∑ i = 1 N α i y i = 0 y i = 1 或 − 1 \begin{aligned} &\max_{\alpha_i} J = \sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)\\ &s.t. \quad \begin{cases}0\le\alpha_i\le C\\\sum_{i=1}^N\alpha_iy_i=0\\y_i=1或-1\end{cases} \end{aligned} αimaxJ=i=1∑Nαi−21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)s.t.⎩⎪⎨⎪⎧0≤αi≤C∑i=1Nαiyi=0yi=1或−1
其中, y i y_i yi和 y j y_j yj分别是第 i i i个和第 j j j个训练集数据向量的标签,易得
y i 2 = 1 y_i^2=1 yi2=1
α i \alpha_i αi和 α j \alpha_j αj是需要优化的变量。
找到分类超平面以后,数据向量 x i x_i xi的预测公式可写为
y i = ω x i + b = ∑ j = 1 N y j α j K i j + b y_i=\omega x_i+b=\sum_{j=1}^Ny_j\alpha_jK_{ij}+b yi=ωxi+b=j=1∑NyjαjKij+b
{ l a b e l i = 1 , y i > 1 l a b e l i = 1 且 x i 是 支 持 向 量 , y i = 1 l a b e l i = 1 且 x i 是 软 间 隔 引 入 的 误 分 类 支 持 向 量 , 0 < y i < 1 l a b e l i 不 存 在 , x i 在 分 类 超 平 面 上 , y i = 0 l a b e l i = − 1 且 x i 是 软 间 隔 引 入 的 误 分 类 支 持 向 量 , − 1 < y i < 0 l a b e l i = − 1 且 x i 是 支 持 向 量 , y i = − 1 l a b e l i = − 1 , y i < − 1 \begin{cases} label_i=1,\quad y_i>1\\ label_i=1且x_i是支持向量, \quad y_i=1\\ label_i=1且x_i是软间隔引入的误分类支持向量, \quad 0
其中, l a b e l i label_i labeli是数据向量 x i x_i xi所属类别。
序列最小优化(SMO)------------------------------------------------------
原始论文:J. C. Platt, Sequential Minimal Optimization:A Fast Algorithm for Training Support Vector Machines (1998) Microsoft Research
传统的SVM凸优化计算效率很低。1998年,来自微软研究院的John C. Platt提出了目前使用最为广泛的快速SVM算法——SMO(Sequential Minimal Optimization,序列最小优化)算法,已用于LibSVM软件包中。该算法每次选择两个 α \alpha α,固定其他 α \alpha α进行优化,直到收敛。
SMO算法实际上与支持向量机本身没有任何关系,它只是一种解决函数凸优化问题的快速方法,所以,该方法的思想一样可以用于解决其他凸函数的凸优化问题。
SMO算法在每一次迭代中,分为内循环和外循环。在外循环中,算法逐一选择每个 α \alpha α。若算法在外循环中的某一步选择了 α i \alpha_i αi,则此时进入内循环,在所有 α \alpha α中选择一个作为 α j \alpha_j αj。
根据《机器学习实战》这本书的介绍:
1、如果 α j \alpha_j αj是随机不重复选择的,则叫做简易SMO算法,此时得到的分类超平面是全局最佳。
2、如果根据原始SMO算法里的启发式方法,若找到一个 α j \alpha_j αj,使得 f ( x j ) − y j f(x_j)-y_j f(xj)−yj与 α i \alpha_i αi的误差 f ( x i ) − y i f(x_i)-y_i f(xi)−yi相差最大,则目标函数就能以最快速度收敛,此时得到的分类超平面是在最佳分类超平面附近,且每次算法得到的分类边界都不一样。
不失一般性,假设在某次迭代中,选择了 α 1 \alpha_1 α1, α 2 \alpha_2 α2,在SVM的目标函数J中,将与 α 1 \alpha_1 α1和 α 2 \alpha_2 α2有关的项单独写出,可构成SMO的目标函数 W S M O W_{SMO} WSMO,为
W S M O = α 1 + α 2 + ∑ i = 3 N α i − [ 1 2 α 1 y 1 ( α 1 y 1 K 11 + α 2 y 2 K 12 + ∑ j = 3 N α j y j K 1 j ) + 1 2 α 2 y 2 ( α 1 y 1 K 21 + α 2 y 2 K 22 + ∑ j = 3 N α j y j K 2 j ) + 1 2 ∑ i = 3 N α i y i ( α 1 y 1 K i 1 + α 2 y 2 K i 2 + ∑ j = 3 N α j y j K i j ) ] = α 1 + α 2 − 1 2 y 1 2 α 1 2 K 11 − y 1 y 2 α 1 α 2 K 12 − 1 2 y 2 2 α 2 2 K 22 − y 1 α 1 ∑ i = 3 N y i α i K 1 i − y 2 α 2 ∑ i = 3 N y i α i K 2 i + A {\begin{aligned} W_{SMO}&=\alpha_1+\alpha_2+\sum_{i=3}^N\alpha_i-\begin{aligned} [&\frac{1}{2}\alpha_1y_1(\alpha_1y_1K_{11}+\alpha_2y_2K_{12}+\sum_{j=3}^N\alpha_jy_jK_{1j})+\\&\frac{1}{2}\alpha_2y_2(\alpha_1y_1K_{21}+\alpha_2y_2K_{22}+\sum_{j=3}^N\alpha_jy_jK_{2j})+\\&\frac{1}{2}\sum_{i=3}^N\alpha_iy_i(\alpha_1y_1K_{i1}+\alpha_2y_2K_{i2}+\sum_{j=3}^N\alpha_jy_jK_{ij})]\end{aligned}\\&=\alpha_1+\alpha_2-\frac{1}{2}y_1^2\alpha_1^2K_{11}-y_1y_2\alpha_1\alpha_2K_{12}-\frac{1}{2}y_2^2\alpha_2^2K_{22}-y_1\alpha_1\sum_{i=3}^Ny_i\alpha_iK_{1i}-y_2\alpha_2\sum_{i=3}^Ny_i\alpha_iK_{2i}+A\end{aligned}} WSMO=α1+α2+i=3∑Nαi−[21α1y1(α1y1K11+α2y2K12+j=3∑NαjyjK1j)+21α2y2(α1y1K21+α2y2K22+j=3∑NαjyjK2j)+21i=3∑Nαiyi(α1y1Ki1+α2y2Ki2+j=3∑NαjyjKij)]=α1+α2−21y12α12K11−y1y2α1α2K12−21y22α22K22−y1α1i=3∑NyiαiK1i−y2α2i=3∑NyiαiK2i+A
其中
A = ∑ i = 3 N α i − 1 2 ∑ i = 3 N ∑ j = 3 N y i y j α i α j K i j A=\sum_{i=3}^N\alpha_i-\frac{1}{2}\sum_{i=3}^N\sum_{j=3}^Ny_iy_j\alpha_i\alpha_jK_{ij} A=i=3∑Nαi−21i=3∑Nj=3∑NyiyjαiαjKij
由于 A A A与 α 1 \alpha_1 α1和 α 2 \alpha_2 α2无关,所以是一个常数,单独写出来。
因此,SVM的目标变为
max α 1 , α 2 W S M O = α 1 + α 2 − 1 2 y 1 2 α 1 2 K 11 − y 1 y 2 α 1 α 2 K 12 − 1 2 y 2 2 α 2 2 K 22 − y 1 α 1 ∑ i = 3 N y i α i K 1 i − y 2 α 2 ∑ i = 3 N y i α i K 2 i + A \begin{aligned} &\max_{\alpha_1,\alpha_2} W_{SMO} = \alpha_1+\alpha_2-\frac{1}{2}y_1^2\alpha_1^2K_{11}-y_1y_2\alpha_1\alpha_2K_{12}-\frac{1}{2}y_2^2\alpha_2^2K_{22}-y_1\alpha_1\sum_{i=3}^Ny_i\alpha_iK_{1i}-y_2\alpha_2\sum_{i=3}^Ny_i\alpha_iK_{2i}+A\end{aligned} α1,α2maxWSMO=α1+α2−21y12α12K11−y1y2α1α2K12−21y22α22K22−y1α1i=3∑NyiαiK1i−y2α2i=3∑NyiαiK2i+A
s . t . { 0 ≤ α i ≤ C ∑ i = 1 N α i y i = 0 y i = 1 或 − 1 s.t. \quad \begin{cases}0\le\alpha_i\le C\\\sum_{i=1}^N\alpha_iy_i=0\\y_i=1或-1\end{cases} s.t.⎩⎪⎨⎪⎧0≤αi≤C∑i=1Nαiyi=0yi=1或−1
现在,可找出 α 1 \alpha_1 α1和 α 2 \alpha_2 α2之间的关系表达式。由 ∑ i = 1 N α i y i = 0 \sum_{i=1}^N\alpha_iy_i=0 ∑i=1Nαiyi=0,则
y 1 α 1 + y 2 α 2 = − ∑ i = 3 N y i α i = ζ y_1\alpha_1+y_2\alpha_2=-\sum_{i=3}^Ny_i\alpha_i=\zeta y1α1+y2α2=−i=3∑Nyiαi=ζ
注意, ζ \zeta ζ是 A A A中的项,所以是常数。两边同乘 y 1 y_1 y1,有 α 1 + y 1 y 2 α 2 = y 1 ζ \alpha_1+y_1y_2\alpha_2=y_1\zeta α1+y1y2α2=y1ζ
即
α 1 = y 1 ζ − y 1 y 2 α 2 ( 1 ) \alpha_1=y_1\zeta-y_1y_2\alpha_2\quad(1) α1=y1ζ−y1y2α2(1)
对于 W S M O W_{SMO} WSMO,令
v 1 = ∑ i = 3 N y i α i K 1 i v_1=\sum_{i=3}^Ny_i\alpha_iK_{1i} v1=i=3∑NyiαiK1i v 2 = ∑ i = 3 N y i α i K 2 i v_2=\sum_{i=3}^Ny_i\alpha_iK_{2i} v2=i=3∑NyiαiK2i
注意, v 1 v_1 v1和 v 2 v_2 v2与 α 1 \alpha_1 α1和 α 2 \alpha_2 α2无关,所以都是常数。则
W S M O = α 1 + α 2 − 1 2 y 1 2 α 1 2 K 11 − y 1 y 2 α 1 α 2 K 12 − 1 2 y 2 2 α 2 2 K 22 − y 1 α 1 v 1 − y 2 α 2 v 2 + A W_{SMO} = \alpha_1+\alpha_2-\frac{1}{2}y_1^2\alpha_1^2K_{11}-y_1y_2\alpha_1\alpha_2K_{12}-\frac{1}{2}y_2^2\alpha_2^2K_{22}-y_1\alpha_1v_1-y_2\alpha_2v_2+A WSMO=α1+α2−21y12α12K11−y1y2α1α2K12−21y22α22K22−y1α1v1−y2α2v2+A
将(1)式代入 W S M O W_{SMO} WSMO,经化简,有
W S M O = y 1 ζ − y 1 y 2 α 2 + α 2 − 1 2 ( ζ − y 2 α 2 ) 2 K 11 − 1 2 α 2 2 K 22 − y 2 α 2 ( ζ − y 2 α 2 ) K 12 − ( ζ − y 2 α 2 ) v 1 − y 2 α 2 v 2 + A W_{SMO}=y_1\zeta -y_1y_2\alpha_2+\alpha_2-\frac{1}{2}(\zeta -y_2\alpha_2)^2K_{11}-\frac{1}{2}\alpha_2^2K_{22}-y_2\alpha_2(\zeta-y_2\alpha_2)K_{12}-(\zeta-y_2\alpha_2)v_1-y_2\alpha_2v_2+A WSMO=y1ζ−y1y2α2+α2−21(ζ−y2α2)2K11−21α22K22−y2α2(ζ−y2α2)K12−(ζ−y2α2)v1−y2α2v2+A
由于 W S M O W_{SMO} WSMO中的量 y 1 , y 2 , ζ , K 11 , K 12 , K 22 , v 1 , v 2 , A y_1,y_2,\zeta,K_{11},K_{12},K_{22},v_1,v_2,A y1,y2,ζ,K11,K12,K22,v1,v2,A都是常量,所以到此,SVM的多元函数优化问题,转化为了一元函数优化问题,即函数 W S M O W_{SMO} WSMO只与 α 2 \alpha_2 α2有关,即
max α 1 , α 2 W S M O = y 1 ζ − y 1 y 2 α 2 + α 2 − 1 2 ( ζ − y 2 α 2 ) 2 K 11 − 1 2 α 2 2 K 22 − y 2 α 2 ( ζ − y 2 α 2 ) K 12 − ( ζ − y 2 α 2 ) v 1 − y 2 α 2 v 2 + A \begin{aligned} &\max_{\alpha_1,\alpha_2} W_{SMO} =y_1\zeta -y_1y_2\alpha_2+\alpha_2-\frac{1}{2}(\zeta -y_2\alpha_2)^2K_{11}-\frac{1}{2}\alpha_2^2K_{22}-y_2\alpha_2(\zeta-y_2\alpha_2)K_{12}-(\zeta-y_2\alpha_2)v_1-y_2\alpha_2v_2+A \end{aligned} α1,α2maxWSMO=y1ζ−y1y2α2+α2−21(ζ−y2α2)2K11−21α22K22−y2α2(ζ−y2α2)K12−(ζ−y2α2)v1−y2α2v2+A s . t . 0 ≤ α 2 ≤ C s.t. \quad 0\le\alpha_2\le C s.t.0≤α2≤C
显然,对于一元函数优化问题,首先需要求函数的一阶导函数,即
d W S M O d α 2 = − y 1 y 2 + 1 + y 2 ( ζ − α 2 y 2 ) K 11 − α 2 K 22 − y 2 ( ζ − 2 α 2 y 2 ) K 12 + y 2 v 1 − y 2 v 2 = 0 \frac{dW_{SMO}}{d\alpha_2}=-y_1y_2+1+y_2(\zeta-\alpha_2y_2)K_{11}-\alpha_2K_{22}-y_2(\zeta-2\alpha_2y_2)K_{12}+y_2v_1-y_2v_2=0 dα2dWSMO=−y1y2+1+y2(ζ−α2y2)K11−α2K22−y2(ζ−2α2y2)K12+y2v1−y2v2=0
经化简,有
d W S M O d α 2 = − y 1 y 2 + 1 − ( K 11 + K 22 − 2 K 12 ) α 2 + y 2 ζ ( K 11 − K 12 ) + y 2 ( v 1 − v 2 ) = 0 \frac{dW_{SMO}}{d\alpha_2}=-y_1y_2+1-(K_{11}+K_{22}-2K_{12})\alpha_2+y_2\zeta(K_{11}-K_{12})+y_2(v_1-v_2)=0 dα2dWSMO=−y1y2+1−(K11+K22−2K12)α2+y2ζ(K11−K12)+y2(v1−v2)=0
注意到, d W S M O d α 2 \frac{dW_{SMO}}{d\alpha_2} dα2dWSMO中的 v 1 v_1 v1和 v 2 v_2 v2形式不够简洁,考察其是否可与前次迭代的结果联系起来,从而减少运算量。
首先,给出SVM对数据向量 x i x_i xi的预测结果 f ( x i ) f(x_i) f(xi)表达式
f ( x i ) = b + ∑ j = 1 N y j α j K i j f(x_i)=b+\sum_{j=1}^Ny_j\alpha_jK_{ij} f(xi)=b+j=1∑NyjαjKij
观察 v 1 v_1 v1和 v 2 v_2 v2的形式,发现其与 f ( x i ) f(x_i) f(xi)较为相似,可对其进行改写,有
v 1 = ∑ i = 3 N y i α i K 1 i = f ( x 1 ) − b − y 1 α 1 K 11 − y 2 α 2 K 12 v_1=\sum_{i=3}^Ny_i\alpha_iK_{1i}=f(x_1)-b-y_1\alpha_1K_{11}-y_2\alpha_2K_{12} v1=i=3∑NyiαiK1i=f(x1)−b−y1α1K11−y2α2K12 v 2 = ∑ i = 3 N y i α i K 2 i = f ( x 2 ) − b − y 1 α 1 K 21 − y 2 α 2 K 22 v_2=\sum_{i=3}^Ny_i\alpha_iK_{2i}=f(x_2)-b-y_1\alpha_1K_{21}-y_2\alpha_2K_{22} v2=i=3∑NyiαiK2i=f(x2)−b−y1α1K21−y2α2K22
必须注意,上述两个式子中的 f ( x 1 ) , f ( x 2 ) , b , α 1 , α 2 f(x_1),f(x_2),b,\alpha_1,\alpha_2 f(x1),f(x2),b,α1,α2都是上一次迭代计算出的结果,为了与本次迭代计算出的所有新变量进行区分,令上一次迭代的 f ( x 1 ) , f ( x 2 ) , b , α 1 , α 2 f(x_1),f(x_2),b,\alpha_1,\alpha_2 f(x1),f(x2),b,α1,α2分别为 f ( x 1 ) o l d , f ( x 2 ) o l d , b o l d , α 1 o l d , α 2 o l d f(x_1)^{old},f(x_2)^{old},b^{old},\alpha_1^{old},\alpha_2^{old} f(x1)old,f(x2)old,bold,α1old,α2old,则
v 1 − v 2 = f ( x 1 ) o l d − f ( x 2 ) o l d − y 1 α 1 o l d ( K 11 − K 21 ) − y 2 α 2 o l d ( K 12 − K 22 ) v_1-v_2=f(x_1)^{old}-f(x_2)^{old}-y_1\alpha_1^{old}(K_{11}-K_{21})-y_2\alpha_2^{old}(K_{12}-K_{22}) v1−v2=f(x1)old−f(x2)old−y1α1old(K11−K21)−y2α2old(K12−K22)
将(1)式代入,消去 α 1 o l d \alpha_1^{old} α1old,同时为统一形式,令 K 12 K_{12} K12表示 K 21 K_{21} K21,化简,有
v 1 − v 2 = f ( x 1 ) o l d − f ( x 2 ) o l d − ζ ( K 11 − K 12 ) + y 2 α 2 o l d ( K 11 + K 22 − 2 K 12 ) v_1-v_2=f(x_1)^{old}-f(x_2)^{old}-\zeta(K_{11}-K_{12})+y_2\alpha_2^{old}(K_{11}+K_{22}-2K_{12}) v1−v2=f(x1)old−f(x2)old−ζ(K11−K12)+y2α2old(K11+K22−2K12)
代入 d W S M O d α 2 \frac{dW_{SMO}}{d\alpha_2} dα2dWSMO,有
d W S M O d α 2 = \begin{aligned}\frac{dW_{SMO}}{d\alpha_2}=\end{aligned} dα2dWSMO=
− y 1 y 2 + 1 − ( K 11 + K 22 − 2 K 12 ) α 2 + y 2 ζ ( K 11 − K 12 ) + y 2 [ f ( x 1 ) o l d − f ( x 2 ) o l d − ζ ( K 11 − K 12 ) + y 2 α 2 o l d ( K 11 + K 22 − 2 K 12 ) ] = 0 \begin{aligned}-y_1y_2+1-(K_{11}+K_{22}-2K_{12})\alpha_2+y_2\zeta(K_{11}-K_{12})+y_2[f(x_1)^{old}-f(x_2)^{old}-\zeta(K_{11}-K_{12})+y_2\alpha_2^{old}(K_{11}+K_{22}-2K_{12})]=0\end{aligned} −y1y2+1−(K11+K22−2K12)α2+y2ζ(K11−K12)+y2[f(x1)old−f(x2)old−ζ(K11−K12)+y2α2old(K11+K22−2K12)]=0
化简,有
d W S M O d α 2 = − y 1 y 2 + 1 − ( K 11 + K 22 − 2 K 12 ) α 2 + y 2 ( f ( x 1 ) o l d − f ( x 2 ) o l d ) + α 2 o l d ( K 11 + K 22 − 2 K 12 ) = 0 \frac{dW_{SMO}}{d\alpha_2}=-y_1y_2+1-(K_{11}+K_{22}-2K_{12})\alpha_2+y_2(f(x_1)^{old}-f(x_2)^{old})+\alpha_2^{old}(K_{11}+K_{22}-2K_{12})=0 dα2dWSMO=−y1y2+1−(K11+K22−2K12)α2+y2(f(x1)old−f(x2)old)+α2old(K11+K22−2K12)=0
令 η = K 11 + K 22 − 2 K 12 \eta=K_{11}+K_{22}-2K_{12} η=K11+K22−2K12,有
d W S M O d α 2 = − y 1 y 2 + 1 − η α 2 + y 2 ( f ( x 1 ) o l d − f ( x 2 ) o l d ) + α 2 o l d η = 0 \frac{dW_{SMO}}{d\alpha_2}=-y_1y_2+1-\eta\alpha_2+y_2(f(x_1)^{old}-f(x_2)^{old})+\alpha_2^{old}\eta=0 dα2dWSMO=−y1y2+1−ηα2+y2(f(x1)old−f(x2)old)+α2oldη=0因 y 2 2 = 1 y_2^2=1 y22=1,则有
d W S M O d α 2 = − y 1 y 2 + y 2 2 + α 2 o l d η − α 2 η + y 2 ( f ( x 1 ) o l d − f ( x 2 ) o l d ) = 0 \frac{dW_{SMO}}{d\alpha_2}=-y_1y_2+y_2^2+\alpha_2^{old}\eta-\alpha_2\eta+y_2(f(x_1)^{old}-f(x_2)^{old})=0 dα2dWSMO=−y1y2+y22+α2oldη−α2η+y2(f(x1)old−f(x2)old)=0
即
d W S M O d α 2 = α 2 o l d η − α 2 η + y 2 ( f ( x 1 ) o l d − f ( x 2 ) o l d − y 1 + y 2 ) = 0 \frac{dW_{SMO}}{d\alpha_2}=\alpha_2^{old}\eta-\alpha_2\eta+y_2(f(x_1)^{old}-f(x_2)^{old}-y_1+y_2)=0 dα2dWSMO=α2oldη−α2η+y2(f(x1)old−f(x2)old−y1+y2)=0
令
E 1 o l d = f ( x 1 ) o l d − y 1 E_1^{old}=f(x_1)^{old}-y_1 E1old=f(x1)old−y1 E 2 o l d = f ( x 2 ) o l d − y 2 E_2^{old}=f(x_2)^{old}-y_2 E2old=f(x2)old−y2
则
d W S M O d α 2 = α 2 o l d η − α 2 η + y 2 ( E 1 o l d − E 2 o l d ) = 0 \frac{dW_{SMO}}{d\alpha_2}=\alpha_2^{old}\eta-\alpha_2\eta+y_2(E_1^{old}-E_2^{old})=0 dα2dWSMO=α2oldη−α2η+y2(E1old−E2old)=0
此时 α 2 \alpha_2 α2的表达式可由上一次迭代计算好的 α 2 o l d \alpha_2^{old} α2old表示,即
α 2 = α 2 o l d + y 2 ( E 1 o l d − E 2 o l d ) η \alpha_2=\alpha_2^{old}+\frac{y_2(E_1^{old}-E_2^{old})}{\eta} α2=α2old+ηy2(E1old−E2old)
到此为止, α 2 \alpha_2 α2计算出来了,但是还从没有考虑过 α 2 \alpha_2 α2的取值范围问题。然而在SVM优化问题中, α i \alpha_i αi的取值范围规定为 0 ≤ α i ≤ C 0\le\alpha_i\le C 0≤αi≤C,且满足 y 1 α 1 + y 2 α 2 = − ∑ i = 3 N y i α i = ζ y_1\alpha_1+y_2\alpha_2=-\sum_{i=3}^Ny_i\alpha_i=\zeta y1α1+y2α2=−∑i=3Nyiαi=ζ。
接下来对 α 2 \alpha_2 α2进行范围限制
接下来,必须对 α 2 \alpha_2 α2的取值范围加以限制,以满足SVM优化问题的约束条件。
已知, y i = 1 或 − 1 y_i=1或-1 yi=1或−1,则 y 1 α 1 + y 2 α 2 = ζ y_1\alpha_1+y_2\alpha_2=\zeta y1α1+y2α2=ζ会出现4种情况,即
{ α 1 + α 2 = ζ α 1 − α 2 = ζ − α 1 + α 2 = ζ − α 1 − α 2 = ζ ⇒ { α 1 = − α 2 + ζ α 1 = α 2 + ζ α 1 = α 2 − ζ α 1 = − α 2 − ζ ⇒ { 0 ≤ − α 2 + ζ ≤ C 0 ≤ α 2 + ζ ≤ C 0 ≤ α 2 − ζ ≤ C 0 ≤ − α 2 − ζ ≤ C ⇒ { ζ − C ≤ α 2 ≤ ζ ① − ζ ≤ α 2 ≤ C − ζ ② ζ ≤ α 2 ≤ C + ζ ③ − ( C + ζ ) ≤ α 2 ≤ − ζ ④ \begin{cases} \alpha_1+\alpha_2=\zeta\\ \alpha_1-\alpha_2=\zeta\\ -\alpha_1+\alpha_2=\zeta\\ -\alpha_1-\alpha_2=\zeta \end{cases} \Rightarrow \begin{cases} \alpha_1=-\alpha_2+\zeta\\ \alpha_1=\alpha_2+\zeta\\ \alpha_1=\alpha_2-\zeta\\ \alpha_1=-\alpha_2-\zeta \end{cases} \Rightarrow \begin{cases} 0\le-\alpha_2+\zeta\le C\\ 0\le\alpha_2+\zeta\le C\\ 0\le\alpha_2-\zeta\le C\\ 0\le-\alpha_2-\zeta\le C \end{cases} \Rightarrow \begin{cases} \zeta-C\le\alpha_2\le\zeta \quad ①\\ -\zeta\le\alpha_2\le C-\zeta \quad ②\\ \zeta\le\alpha_2\le C+\zeta \quad ③\\ -(C+\zeta)\le\alpha_2\le -\zeta \quad ④\\ \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧α1+α2=ζα1−α2=ζ−α1+α2=ζ−α1−α2=ζ⇒⎩⎪⎪⎪⎨⎪⎪⎪⎧α1=−α2+ζα1=α2+ζα1=α2−ζα1=−α2−ζ⇒⎩⎪⎪⎪⎨⎪⎪⎪⎧0≤−α2+ζ≤C0≤α2+ζ≤C0≤α2−ζ≤C0≤−α2−ζ≤C⇒⎩⎪⎪⎪⎨⎪⎪⎪⎧ζ−C≤α2≤ζ①−ζ≤α2≤C−ζ②ζ≤α2≤C+ζ③−(C+ζ)≤α2≤−ζ④
在四种情况中,只有 ζ \zeta ζ是变化的,现在需要讨论在不同 ζ \zeta ζ下的情况。
A. 对于情况①, y 1 = y 2 = 1 y_1=y_2=1 y1=y2=1,方程为 α 1 = − α 2 + ζ \alpha_1=-\alpha_2+\zeta α1=−α2+ζ,绘制出其图像
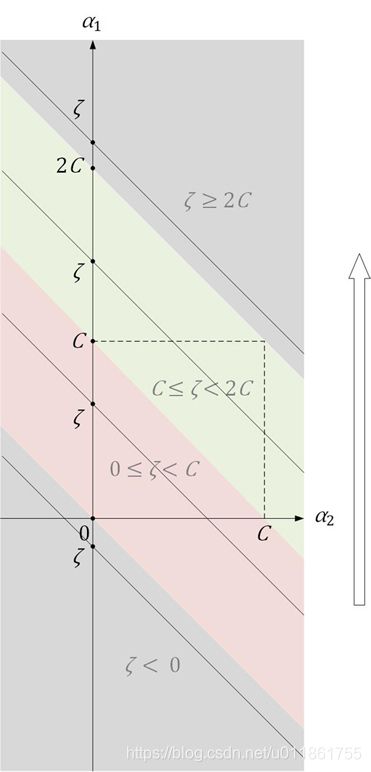
图中,直线 α 1 = − α 2 + ζ \alpha_1=-\alpha_2+\zeta α1=−α2+ζ从下到上扫过方形区域, ζ \zeta ζ是直线与 α 1 \alpha_1 α1轴的交点,即直线的截距。由图知,可以将 ζ \zeta ζ的取值范围分为四个部分看待:
ζ < 0 , 0 ≤ ζ < C , C ≤ ζ < 2 C , 2 C ≤ ζ \zeta<0,\quad 0\le\zeta
1、当 ζ < 0 \zeta<0 ζ<0时,为图中最下面的那条直线的情况,直线与方形区域没有交点。将 ζ < 0 \zeta<0 ζ<0代入①式,有 ζ − C < 0 \zeta-C<0 ζ−C<0,则
( ζ − C ≤ α 2 ≤ ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = ∅ (\zeta-C\le\alpha_2\le\zeta)\cap(0\le\alpha_2\le C)=\varnothing (ζ−C≤α2≤ζ)∩(0≤α2≤C)=∅
2、当 0 ≤ ζ < C 0\le\zeta
( ζ − C ≤ α 2 ≤ ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = 0 ≤ α 2 ≤ ζ (\zeta-C\le\alpha_2\le\zeta)\cap(0\le\alpha_2\le C)=0\le\alpha_2\le\zeta (ζ−C≤α2≤ζ)∩(0≤α2≤C)=0≤α2≤ζ
3、当 C ≤ ζ < 2 C C\le\zeta<2C C≤ζ<2C时,直线扫过方形区域上半部分。将 C ≤ ζ < 2 C C\le\zeta<2C C≤ζ<2C代入①式,有 0 ≤ ζ − C < C 0\le\zeta-C
( ζ − C ≤ α 2 ≤ ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = ζ − C ≤ α 2 ≤ C (\zeta-C\le\alpha_2\le\zeta)\cap(0\le\alpha_2\le C)=\zeta-C\le\alpha_2\le C (ζ−C≤α2≤ζ)∩(0≤α2≤C)=ζ−C≤α2≤C
4、当 2 C ≤ ζ 2C\le\zeta 2C≤ζ时,为图中最上方的直线的情况,直线与方形区域没有交点。将 2 C ≤ ζ 2C\le\zeta 2C≤ζ代入①式,有 C ≤ ζ − C C\le\zeta-C C≤ζ−C,则
( ζ − C ≤ α 2 ≤ ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = ∅ (\zeta-C\le\alpha_2\le\zeta)\cap(0\le\alpha_2\le C)=\varnothing (ζ−C≤α2≤ζ)∩(0≤α2≤C)=∅
综上,有
{ ∅ , ζ < 0 0 ≤ α 2 ≤ ζ , 0 ≤ ζ < C ζ − C ≤ α 2 ≤ C , C ≤ ζ < 2 C ∅ , 2 C ≤ ζ \begin{cases} \varnothing,\quad\zeta<0\\ 0\le\alpha_2\le\zeta,\quad0\le\zeta
将该不等式组写成一个不等式,有
m a x ( 0 , ζ − C ) ≤ α 2 ≤ m i n ( ζ , C ) max(0,\zeta-C)\le\alpha_2\le min(\zeta,C) max(0,ζ−C)≤α2≤min(ζ,C)
注意到,对于情况①,虽然 α 1 + α 2 = ζ \alpha_1+\alpha_2=\zeta α1+α2=ζ,但是此时的 α 2 \alpha_2 α2没有完全计算完,而对 α 2 \alpha_2 α2的范围规定又需要 ζ \zeta ζ,这就造成了矛盾。为了避免这种情况,令 α 1 o l d + α 2 o l d = ζ \alpha_1^{old}+\alpha_2^{old}=\zeta α1old+α2old=ζ,则
m a x ( 0 , α 1 o l d + α 2 o l d − C ) ≤ α 2 ≤ m i n ( α 1 o l d + α 2 o l d , C ) max(0,\alpha_1^{old}+\alpha_2^{old}-C)\le\alpha_2\le min(\alpha_1^{old}+\alpha_2^{old},C) max(0,α1old+α2old−C)≤α2≤min(α1old+α2old,C)
B. 对于情况②, y 1 = 1 , y 2 = − 1 y_1=1,y_2=-1 y1=1,y2=−1,方程为 α 1 = α 2 + ζ \alpha_1=\alpha_2+\zeta α1=α2+ζ,绘制出其图像
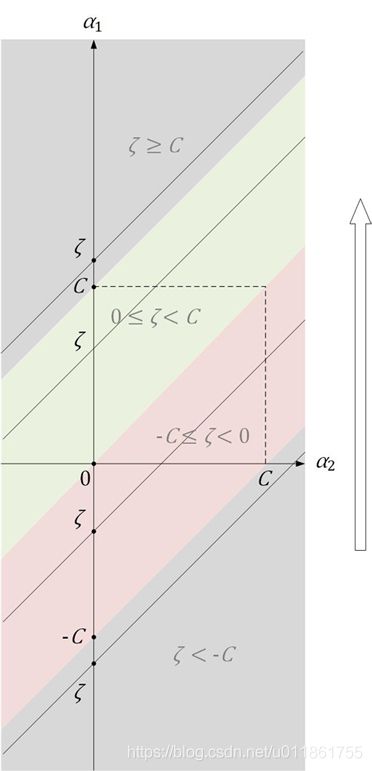
图中,直线 α 1 = α 2 + ζ \alpha_1=\alpha_2+\zeta α1=α2+ζ从下到上扫过方形区域, ζ \zeta ζ是直线与 α 1 \alpha_1 α1轴的交点,即直线的截距。由图知,可以将 ζ \zeta ζ的取值范围分为四个部分看待:
ζ < − C , − C ≤ ζ < 0 , 0 ≤ ζ < C , C ≤ ζ \zeta<-C,\quad -C\le\zeta<0,\quad 0\le\zeta
1、当 ζ < − C \zeta<-C ζ<−C时,为图中最下面的那条直线的情况,直线与方形区域没有交点。将 ζ < − C \zeta<-C ζ<−C代入②式,有 − ζ > C -\zeta>C −ζ>C, C − ζ > 2 C C-\zeta>2C C−ζ>2C,则
( − ζ ≤ α 2 ≤ C − ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = ∅ (-\zeta\le\alpha_2\le C-\zeta)\cap(0\le\alpha_2\le C)=\varnothing (−ζ≤α2≤C−ζ)∩(0≤α2≤C)=∅
2、当 − C ≤ ζ < 0 -C\le\zeta<0 −C≤ζ<0时,直线扫过方形区域下半部分。将 − C ≤ ζ < 0 -C\le\zeta<0 −C≤ζ<0代入②式,有 0 < − ζ ≤ C 0<-\zeta\le C 0<−ζ≤C, C < C − ζ ≤ 2 C C
( − ζ ≤ α 2 ≤ C − ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = − ζ ≤ α 2 ≤ C (-\zeta\le\alpha_2\le C-\zeta)\cap(0\le\alpha_2\le C)=-\zeta\le\alpha_2\le C (−ζ≤α2≤C−ζ)∩(0≤α2≤C)=−ζ≤α2≤C
3、当 0 ≤ ζ < C 0\le\zeta
( − ζ ≤ α 2 ≤ C − ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = 0 ≤ α 2 ≤ C − ζ (-\zeta\le\alpha_2\le C-\zeta)\cap(0\le\alpha_2\le C)=0\le\alpha_2\le C-\zeta (−ζ≤α2≤C−ζ)∩(0≤α2≤C)=0≤α2≤C−ζ
4、当 C ≤ ζ C\le\zeta C≤ζ时,为图中最上方的直线的情况,直线与方形区域没有交点。将 2 C ≤ ζ 2C\le\zeta 2C≤ζ代入②式,有 − ζ ≤ − 2 C -\zeta\le -2C −ζ≤−2C, C − ζ ≤ − C C-\zeta\le-C C−ζ≤−C则
( − ζ ≤ α 2 ≤ C − ζ ) ∩ ( 0 ≤ α 2 ≤ C ) = ∅ (-\zeta\le\alpha_2\le C-\zeta)\cap(0\le\alpha_2\le C)=\varnothing (−ζ≤α2≤C−ζ)∩(0≤α2≤C)=∅
综上,有
{ ∅ , ζ < − C − ζ ≤ α 2 ≤ C , − C ≤ ζ < 0 0 ≤ α 2 ≤ C − ζ , 0 ≤ ζ < C ∅ , C ≤ ζ \begin{cases} \varnothing,\quad\zeta<-C\\ -\zeta\le\alpha_2\le C,\quad-C\le\zeta<0\\ 0\le\alpha_2\le C-\zeta,\quad 0\le\zeta
将该不等式组写成一个不等式,有
m a x ( 0 , − ζ ) ≤ α 2 ≤ m i n ( C , C − ζ ) max(0,-\zeta)\le\alpha_2\le min(C,C-\zeta) max(0,−ζ)≤α2≤min(C,C−ζ)
将②式中的 α 1 o l d − α 2 o l d = ζ \alpha_1^{old}-\alpha_2^{old}=\zeta α1old−α2old=ζ代入,有
m a x ( 0 , α 2 o l d − α 1 o l d ) ≤ α 2 ≤ m i n ( C , C + α 2 o l d − α 1 o l d ) max(0,\alpha_2^{old}-\alpha_1^{old})\le\alpha_2\le min(C,C+\alpha_2^{old}-\alpha_1^{old}) max(0,α2old−α1old)≤α2≤min(C,C+α2old−α1old)
C. 对于情况③, y 1 = − 1 , y 2 = 1 y_1=-1,y_2=1 y1=−1,y2=1,方程为 α 1 = α 2 − ζ \alpha_1=\alpha_2-\zeta α1=α2−ζ,可以发现方程中的 − ζ -\zeta −ζ与情况②的 ζ \zeta ζ差一个负号,所以只需将 − ζ -\zeta −ζ代替情况②中的所有 ζ \zeta ζ,即可得到
m a x ( 0 , ζ ) ≤ α 2 ≤ m i n ( C , C + ζ ) max(0,\zeta)\le\alpha_2\le min(C,C+\zeta) max(0,ζ)≤α2≤min(C,C+ζ)
将③式中的 − α 1 o l d + α 2 o l d = ζ -\alpha_1^{old}+\alpha_2^{old}=\zeta −α1old+α2old=ζ代入,有
m a x ( 0 , α 2 o l d − α 1 o l d ) ≤ α 2 ≤ m i n ( C , C + α 2 o l d − α 1 o l d ) max(0,\alpha_2^{old}-\alpha_1^{old})\le\alpha_2\le min(C,C+\alpha_2^{old}-\alpha_1^{old}) max(0,α2old−α1old)≤α2≤min(C,C+α2old−α1old)
D. 对于情况④, y 1 = y 2 = − 1 y_1=y_2=-1 y1=y2=−1,方程为 α 1 = − α 2 − ζ \alpha_1=-\alpha_2-\zeta α1=−α2−ζ,可以发现方程中的 − ζ -\zeta −ζ与情况①的 ζ \zeta ζ差一个负号,所以只需将 − ζ -\zeta −ζ代替情况①中的所有 ζ \zeta ζ,即可得到
m a x ( 0 , − ζ − C ) ≤ α 2 ≤ m i n ( − ζ , C ) max(0,-\zeta-C)\le\alpha_2\le min(-\zeta,C) max(0,−ζ−C)≤α2≤min(−ζ,C)
将④式中的 − α 1 o l d − α 2 o l d = ζ -\alpha_1^{old}-\alpha_2^{old}=\zeta −α1old−α2old=ζ代入,有
m a x ( 0 , α 1 o l d + α 2 o l d − C ) ≤ α 2 ≤ m i n ( α 1 o l d + α 2 o l d , C ) max(0,\alpha_1^{old}+\alpha_2^{old}-C)\le\alpha_2\le min(\alpha_1^{old}+\alpha_2^{old},C) max(0,α1old+α2old−C)≤α2≤min(α1old+α2old,C)
综上讨论,可以得到 α 2 \alpha_2 α2的取值范围,即
{ m a x ( 0 , α 1 o l d + α 2 o l d − C ) ≤ α 2 ≤ m i n ( α 1 o l d + α 2 o l d , C ) , y 1 = y 2 m a x ( 0 , α 2 o l d − α 1 o l d ) ≤ α 2 ≤ m i n ( C , C + α 2 o l d − α 1 o l d ) , y 1 ≠ y 2 \begin{cases} max(0,\alpha_1^{old}+\alpha_2^{old}-C)\le\alpha_2\le min(\alpha_1^{old}+\alpha_2^{old},C),\quad y_1=y_2\\ max(0,\alpha_2^{old}-\alpha_1^{old})\le\alpha_2\le min(C,C+\alpha_2^{old}-\alpha_1^{old}),\quad y_1\neq y_2\\ \end{cases} {max(0,α1old+α2old−C)≤α2≤min(α1old+α2old,C),y1=y2max(0,α2old−α1old)≤α2≤min(C,C+α2old−α1old),y1=y2
将 α 2 \alpha_2 α2按照上述范围进行裁剪,任何大于或小于上下界的 α 2 \alpha_2 α2都强制赋值为上界的值或下界的值。
现在完成了对 α 2 \alpha_2 α2的完整计算。
由 α 1 \alpha_1 α1和 α 2 \alpha_2 α2之间的关系表达式 y 1 α 1 + y 2 α 2 = ζ = − ∑ i = 3 N y i α i y_1\alpha_1+y_2\alpha_2=\zeta=-\sum_{i=3}^Ny_i\alpha_i y1α1+y2α2=ζ=−∑i=3Nyiαi,有
α 1 = y 1 ζ − y 1 y 2 α 2 \alpha_1=y_1\zeta-y_1y_2\alpha_2 α1=y1ζ−y1y2α2
现在,需要对 ζ \zeta ζ进行表达。
在本次迭代中, ζ = − ∑ i = 3 N y i α i \zeta=-\sum_{i=3}^Ny_i\alpha_i ζ=−∑i=3Nyiαi始终与 α 1 和 α 2 \alpha_1和\alpha_2 α1和α2无关,所以 ζ \zeta ζ是常数,没有发生变化,所以 y 1 α 1 + y 2 α 2 = y 1 α 1 o l d + y 2 α 2 o l d y_1\alpha_1+y_2\alpha_2=y_1\alpha_1^{old}+y_2\alpha_2^{old} y1α1+y2α2=y1α1old+y2α2old,所以有
α 1 = α 1 o l d + y 1 y 2 ( α 2 o l d − α 1 o l d ) \alpha_1=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_1^{old}) α1=α1old+y1y2(α2old−α1old)
计算出了 α 1 \alpha_1 α1和 α 2 \alpha_2 α2后,就可以计算偏置 b b b了。
现在开始计算偏置 b b b
若 0 < α 1 < C 0<\alpha_1
y 1 ( ω x 1 + b 1 ) = 1 y_1(\omega x_1+b_1)=1 y1(ωx1+b1)=1
即
y 1 y 1 ( ω x 1 + b 1 ) = y 1 y_1y_1(\omega x_1+b_1)=y_1 y1y1(ωx1+b1)=y1
即
ω x 1 + b 1 = y 1 \omega x_1+b_1=y_1 ωx1+b1=y1
即
f ( x 1 ) = ∑ i = 1 N y i α i K 1 i + b 1 = y 1 α 1 K 11 + y 2 α 2 K 12 + ∑ i = 3 N y i α i K 1 i + b 1 = y 1 f(x_1)=\sum_{i=1}^Ny_i\alpha_iK_{1i}+b_1=y_1\alpha_1K_{11}+y_2\alpha_2K_{12}+\sum_{i=3}^Ny_i\alpha_iK_{1i}+b_1=y_1 f(x1)=i=1∑NyiαiK1i+b1=y1α1K11+y2α2K12+i=3∑NyiαiK1i+b1=y1
则
b 1 = y 1 − y 1 α 1 K 11 − y 2 α 2 K 12 − ∑ i = 3 N y i α i K 1 i b_1=y_1-y_1\alpha_1K_{11}-y_2\alpha_2K_{12}-\sum_{i=3}^Ny_i\alpha_iK_{1i} b1=y1−y1α1K11−y2α2K12−i=3∑NyiαiK1i
又
y 1 − ∑ i = 3 N y i α i K 1 i = y 1 + f ( x 1 ) o l d − f ( x 1 ) o l d − ∑ i = 3 N y i α i K 1 i y_1-\sum_{i=3}^Ny_i\alpha_iK_{1i}=y_1+f(x_1)^{old}-f(x_1)^{old}-\sum_{i=3}^Ny_i\alpha_iK_{1i} y1−i=3∑NyiαiK1i=y1+f(x1)old−f(x1)old−i=3∑NyiαiK1i
即
y 1 − ∑ i = 3 N y i α i K 1 i = y 1 − f ( x 1 ) o l d + y 1 α 1 o l d K 11 + y 2 α 2 o l d K 12 + ∑ i = 3 N y i α i K 1 i + b 1 o l d − ∑ i = 3 N y i α i K 1 i y_1-\sum_{i=3}^Ny_i\alpha_iK_{1i}=y_1-f(x_1)^{old}+y_1\alpha_1^{old}K_{11}+y_2\alpha_2^{old}K_{12}+\sum_{i=3}^Ny_i\alpha_iK_{1i}+b_1^{old}-\sum_{i=3}^Ny_i\alpha_iK_{1i} y1−i=3∑NyiαiK1i=y1−f(x1)old+y1α1oldK11+y2α2oldK12+i=3∑NyiαiK1i+b1old−i=3∑NyiαiK1i
令 E 1 o l d = f ( x 1 ) o l d − y 1 E_1^{old}=f(x_1)^{old}-y_1 E1old=f(x1)old−y1,则
y 1 − ∑ i = 3 N y i α i K 1 i = b 1 o l d − E 1 o l d + y 1 α 1 o l d K 11 + y 2 α 2 o l d K 12 y_1-\sum_{i=3}^Ny_i\alpha_iK_{1i}=b_1^{old}-E_1^{old}+y_1\alpha_1^{old}K_{11}+y_2\alpha_2^{old}K_{12} y1−i=3∑NyiαiK1i=b1old−E1old+y1α1oldK11+y2α2oldK12
代回 b 1 b_1 b1的表达式,有
b = b 1 = b 1 o l d − E 1 o l d + y 1 ( α 1 o l d − α 1 ) K 11 + y 2 ( α 2 o l d − α 2 ) K 12 b=b_1=b_1^{old}-E_1^{old}+y_1(\alpha_1^{old}-\alpha_1)K_{11}+y_2(\alpha_2^{old}-\alpha_2)K_{12} b=b1=b1old−E1old+y1(α1old−α1)K11+y2(α2old−α2)K12
若 0 < α 2 < C 0<\alpha_2
b = b 2 = b 2 o l d − E 2 o l d + y 1 ( α 2 o l d − α 2 ) K 21 + y 2 ( α 2 o l d − α 2 ) K 12 b=b_2=b_2^{old}-E_2^{old}+y_1(\alpha_2^{old}-\alpha_2)K_{21}+y_2(\alpha_2^{old}-\alpha_2)K_{12} b=b2=b2old−E2old+y1(α2old−α2)K21+