【原创】【论文复现】【Matlab】【图像处理】基于高斯尺度空间下的自适应阈值分割算法

参考文献：
[1] 龙建武, 闫何, 张建勋, 田芳, 等. 智能图像分割技术[M]. 北京: 科学出版社. 2017
[2] 龙建武, 申铉京, 臧慧, 陈海鹏. 高斯尺度空间下估计背景的自适应阈值分割算法[J]. 自动化学报, 40(8), 2014: 1773-1782. DOI: 10.3724/SP.J.1004.2014.01773

概述

对于背景亮度分布不均匀的图像，直接进行全局阈值分割很难将目标图像区域分割出来。对此，[2]中提出，可以通过高斯尺度空间对背景进行估计，得到大致背景图像，再用原图减去估计的背景，得到目标图像，通过伽马校正突出目标图像后，最后使用Otsu算法进行全局分割，得到目标图像。
本文是对[2]的复现。

细节：

1、 高斯尺度空间：

类比图像金字塔，本文通过给定一个初始sigma值与迭代步长后，迭代出多张高斯模糊的图像。例如给定初始sigma为1，步长为sqrt(2)*sigma，则第一层的sigma=1，第二层的sigma=sqrt(2)，第三层的sigma=sqrt(2)*sqrt(2)，以此类推，从而构造出模糊程度越来越大的图像堆叠。随着迭代的进行，尺度空间的层数也在增加，为了适当地结束迭代，[1]中规定使用最后一层与前一层之间的平均差值来确定迭代是否需要结束，公式如下：
$${\Delta }_i=\frac{1}{MN}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}|L_{i+1}(x,y,{\sigma }_{i+1})-L_i(x,y,{\sigma }_i)|$$
其中$L_i$表示第i层的高斯图像，M和N表示图像的长和宽，x和y表示图像在长和宽上的每个像素。
当上式小于某个阈值，例如$10^{-6}$时，则迭代停止。
高斯尺度空间中第i层图像的权值${\omega }_i$由如下公式给出：
$${\omega }_i=\frac{i+1}{{\sum }_{i=0}^{n-1}(i+1)}$$
本文采用的卷积窗大小为原始图像尺寸中短边的长度，初始$\sigma$=25，最大迭代数为25，迭代步长为sqrt(2)。
下图为原始图像：

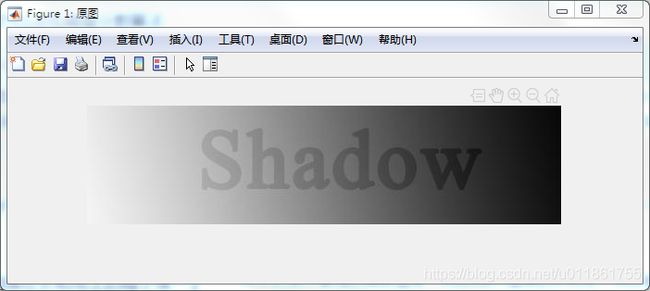
下图为高斯尺度空间的最顶层图像：

2、目标图像的提取：

构建完高斯尺度空间后，[1]在每层中用原始图像减去对应层的高斯图像，取绝对值，得到每层的目标图像，再通过下式，得到最终的目标图像：
$$D(x,y)=\sum _{i=0}^{n-1}{\omega }_i{D}_i(x,y)$$
其中，$D_i$为每层的目标图像。
由于目标图像比较暗，[1]使用了伽玛校正来提高目标图像的亮度。

下图为原始图像的直方图：

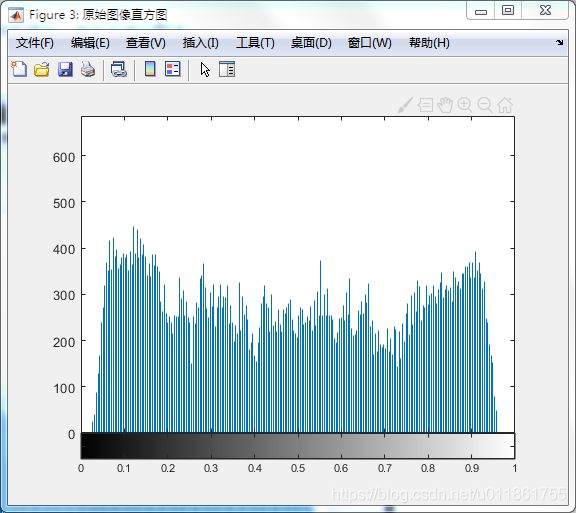
可以看到直方图分布杂乱无章，无法找到低谷。

对原始图像直接使用Otsu对原始图像进行分割：

下图为提取出的原始目标图像：

原始目标图像直方图：

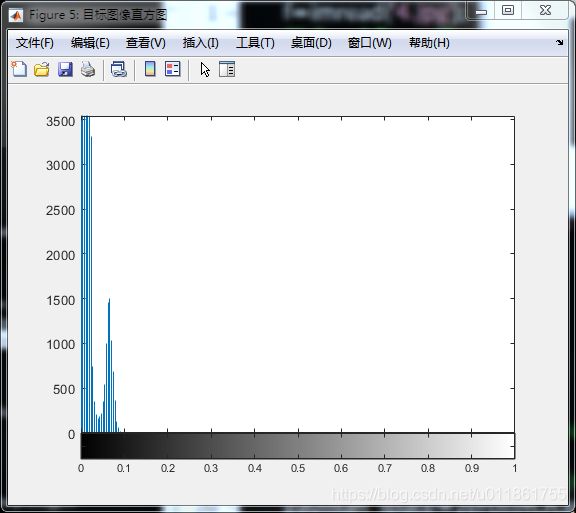
可以看到直方图出现了深谷，非常适合分割。
对图像进行伽玛校正，提高对比度，选择$\gamma$=1.3：

3、直接使用Otsu全局分割

可以看出效果非常理想，达到了预期目标。

输入图像：4.jpg

代码：

close all
clear all
f=imread('4.jpg');
% f=rgb2gray(f);
f=double(f);
f=f/255;
[m,n]=size(f);
figure('Name','原图'),imshow(f);
otsu_thresh=graythresh(f);
figure('Name','直接使用Otsu法分割'),imshow(f>=otsu_thresh);
figure('Name','原始图像直方图'),imhist(f);
%创建二维高斯尺度空间
%设置最大迭代次数
epoch=30;
%设置初始标准差
sigma=25;
%设置卷积窗大小
h=min(m,n);
%设置每层之间标准差的倍数
k=sqrt(2);
%初始化保存高斯尺度空间的矩阵
gaussian_space=zeros(m,n,epoch);
%高斯尺度空间的第一层
G=fspecial('gaussian',[h h],sigma);
gaussian_space(:,:,1)=imfilter(f,G,'replicate');
for i=2:epoch+1
    %更新sigma
    sigma=k*sigma;  
    %计算高斯卷积窗
    G=fspecial('gaussian',[h h],sigma);
    %高斯卷积
    gaussian_space(:,:,i)=imfilter(f,G,'replicate');
    %计算每两层之间的平均差值
    error=sum(abs(gaussian_space(:,:,i)-gaussian_space(:,:,i-1)),'all')/(m*n);
    %如果差值小于一个指定的阈值，则将前一层指定为估计的背景
    if error<=0.00001
        estim_background=gaussian_space(:,:,i-1);
        layer_num=i;
        break;
    end
    if i==epoch+1
        error('设置的最大迭代次数不够');
    end
end
figure('Name','高斯尺度空间的最顶层图像'),imshow(estim_background);
%计算各层目标图像的权值
omega=zeros(i-1,1);
for k=1:i-1
    omega(k)=k/sum(1:i-1);
end
%保存各层的目标图像
target=zeros(m,n,k);
for a=1:k
    target(:,:,a)=abs(f-gaussian_space(:,:,a));
end
%得到最终的目标图像
target_end=zeros(m,n);
for b=1:k
    target_end=omega(b)*target(:,:,b)+target_end;
end
figure('Name','目标图像直方图'),imhist(target_end);
figure('Name','目标图像'),imshow(target_end);
%对目标图像进行GAMMA校正，突出目标信息
target_end=target_end.^1.3;
figure('Name','Gamma校正后的图像'),imshow(target_end);
%对GAMMA校正后的图像进行OTSU阈值分割
otsu_target=graythresh(target_end);
figure('Name','最终的分割图'),imshow(target_end>=otsu_target);