Stanford 机器学习笔记 Week8 Dimensionality Reduction
Motivation
Motivation I: Data Compression
降维可以做数据压缩,减少冗余信息从而减小存储空间。
2D向1D降维:

cm 和 inches都表示长度,属于冗余信息,可以用z向量做新的维度,用1维就可以表示长度。
3D向2D降维:

在左侧的原始数据中,所有点都接近一个平面,这说明存在冗余维度。将所有点投影到该平面形成中间图。用向量z1,z2做新的维度,降到2维。
Motivation II: Visualization
降维还可以用于可视化。
因为人类能理解的只有2维或3维图像,因此如果能把数据集降到<=3维的情况,就可以绘出人能理解的图像。
在这种情况下,每个维度没有具体的意义,它的意义是多个正相关属性共同决定的。
Principal Component Analysis
Principal Component Analysis Problem Formulation
projection error指的是原training set的每个点到降维后投影的点的距离之和。
主成分分析(PCA)的定义就是:
将高维数据降为K维数据时,找到K个向量(构成K维),使得training set到这个K维平面的projection error最小。
对于2D to 1D问题,就是找一条直线使得数据集中每个点到该直线距离之和最小。
注意这和linear regression是不一样的:
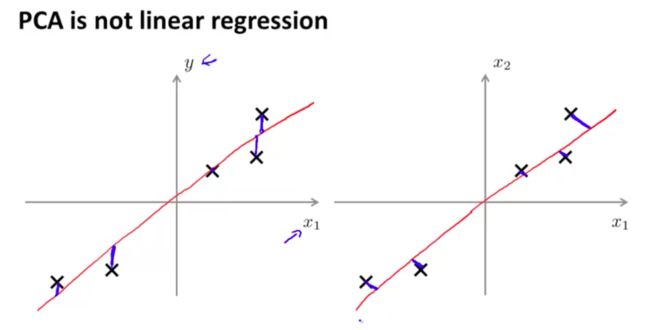
左图是Linear Regression,每个点的cost是该点按y轴方向到直线的距离。而右图PCA就是点到直线的距离。
Principal Component Analysis Algorithm
PCA算法步骤:
1.做归一化:
x(i)j = (x(i)j - uj)/sj
其中x(i)j是第i个数据的第j个属性值,uj是所有数据第j个属性的平均值,sj表示数据离散情况,可以用所有数据第j个属性的max-min或标准差。
2.计算covariance(共变)矩阵sigma
3.对sigma做奇异值分解(SVD)

SVD得到3个矩阵,我们使用第一个矩阵U,这也是一个n*n的矩阵。
这一步的意义:
转自http://blog.csdn.net/abcjennifer/article/details/7758797:
在matlab中有函数[U,S,V] = svd(A) 返回一个与A同大小的对角矩阵S(由Σ的特征值组成),两个酉矩阵U和V,且满足Σ= U*S*V’。若A为m×n阵,则U为m×m阵,V为n×n阵。奇异值在S的对角线上,非负且按降序排列。
那么对于方阵Σ呢,就有
Σ = USV’
ΣΣ’ = USV’*VS’U’ = U(ΣΣ’)U’
Σ’Σ = VS’U’*USV’ = V(Σ’Σ)V’
i.e. U是ΣΣ’的特征向量矩阵;V是Σ’Σ的特征向量矩阵,都是n*n的矩阵
由于方阵的SVD相当于特征值分解,所以事实上U = V, 即Σ = USU’, U是特征向量组成的正交矩阵
我们的目的是,从n维降维到k维,也就是选出这n个特征中最重要的k个,也就是选出特征值最大的k个
4.因为SVD后S对角矩阵已经是按特征值排过序的了,因此U的前k个特征向量就是最重要的k个,将它们截取出来得到Ureduce

之后如果我们想把一个n维向量x(i)转成k维向量,就用Ureduce(T) * x(i)就完成了降维。
Applying PCA
Reconstruction from Compressed Representation
把降维后的向量还原回去的方法很简单,上一节已经求出Ureduce了,直接用Ureduce*降维后向量就还原了Xapprox(i),这个值接近于原x(i)。
Chosing the Number of Principle Components
如何选择K使得可以尽可能降到一个很低的维度同时不丢失太多信息?
如下图,提出两个定义:

如果满足这个性质就说明99%的信息都没丢失。
可以通过从小到大枚举K,计算上面的公式,令K等于第一个满足上面条件的值。

如上图,需要check的公式可以变换为另一个公式(右侧),该公式仅使用SVD后计算出的S矩阵中的特征值。
Advice for Applying PCA
PCA可以用来加速机器学习算法。因为降维之后数据集大小减小,这可以显著减少算法运行时间。
不要用PCA来防止过拟合
因为PCA减少了属性的数量,一定程度可以减小过拟合。但是PCA付出的代价是丢失信息,即使丢失的很少这也是没必要的,因为使用regularization可以保证100%不丢失信息。
仅当算法在原数据集上的运行时间或存储空间无法实现,再采用PCA,不要开始就使用PCA